Жданов Основы физических процессов 2007

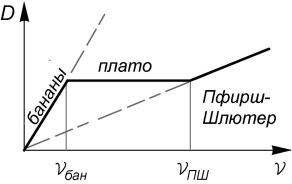
Сами «бананы» могут существовать, не разрушаясь, пока частота столкновений достаточно мала

В обоих режимах и частых столкновений, ν > νПШ , и редких столкновений, ν < νбан , коэффициент диффузии, очевидно, прямо

пропорционален частоте столкновений (см. рис. 2.17), но угловой коэффициент этой пропорциональности существенно разный. В промежуточной области частот, когда «бананы» уже разрушаются, но столкновения ещё редкие, основной вклад в диффузию дают медленные пролетные частицы, а коэффициент диффузии почти не зависит от частоты столкновений − это режим плато. Величину коэффициента диффузии в режиме плато можно оценить, подставив в формулу Пфирша-Шлютера вместо частоты столкновений

ν = νПШ .

Превышение коэффициента диффузии над его классическим значением получило название неоклассической диффузии, а теория Галеева и Сагдеева, объясняющая причину этого превышения, на-

зывается неоклассической теорией диффузии, или, кратко, неоклас-

сикой. Эксперименты подтверждают эту неоклассическую теорию.

Рис. 2.17. Зависимость «неоклассического» коэффициента диффузии от частоты столкновений

121

Теплопроводность

С точки зрения элементарной газокинетической теории коэффициент теплопроводности пропорционален коэффициенту диффузии, умноженному на плотность (1.61):

κ = Dn.

Это правило может быть формально применено к плазме, как для вычисления κ||, так и для κ . Следует лишь учесть, что в отличие от диффузии, возможной лишь при столкновении разнородных частиц, в переносе тепла, напротив, главную роль играют столкновения одинаковых частиц. Следует иметь в виду, что при заданной плотности коэффициент теплопроводности вдоль магнитного поля κ||, согласно выражениям (2.80) и (1.61), пропорционален длине свободного пробега частицы и в максвеллизованной плазме больше для электронов (примерно в корень из отношения масс, ~(mi/me)1/2, раз) , а коэффициент теплопроводности поперек магнитного поля,

согласно выражению (2.82), больше для ионов (также примерно в корень из отношения масс, ~(mi/me)1/2, раз).

Таким образом, согласно классическим представлениям, в замагниченной плазме вдоль магнитного поля тепло переносят главным образом электроны, а поперек магнитного поля − ионы.

Отметим, что неоклассические соображения могут быть перенесены и на теплопроводность. Особенности движения частиц в поле сложной геометрии и здесь приводят к изменению величины коэффициента процесса переноса тепла. Правда, в экспериментах на токамаках наблюдается аномально большой по сравнению с неоклассическим теплоперенос электронами.

Проводимость плазмы в магнитном поле

• Проводимость плазмы вдоль магнитного поля

Наложение на плазму магнитного поля не оказывает влияния на движение частиц вдоль поля и, следовательно, не влияет на продольную проводимость, определяемую составляющей электрического поля, направленной параллельно магнитному полю:

122

где σ0 - проводимость плазмы в отсутствие магнитного поля.

• Поляризация плазмы

Если плазму, находящуюся в магнитном поле, поместить в электрическое поле Е, перпендикулярное к магнитному полю, то согласно дрейфовым представлениям у электронов и ионов появит-

E

ся одинаковая скорость vE = c B . Поэтому тока не будет, однако,

произойдет некоторое разделение зарядов − плазма поляризуется: частицы будут двигаться по трохоидам, смещаясь от первоначального положения на некоторые величины e, i. Если пренебречь тепловой скоростью, приняв начальную скорость равной нулю, то трохоида вырождается в циклоиду (см. рис. 2.2), а величина среднего смещения e,i будет равна ларморовскому радиусу, который следует вычислять по величине дрейфовой скорости.

Пусть вектор напряженности магнитного поля В направлен вдоль оси Z системы координат, а вектор напряженности электрического поля Е - вдоль оси Y (см. рис.2.18). Скорость дрейфа в скрещенных электрическом и магнитном полях будет направлена параллельно оси X. Модули средних смещений для электрона < e> и иона < i> равны соответственно:

E

где vE = c B , а заряды частиц по величине считаются одинаковыми.

Умножив эту величину на заряд и на плотность, получим дипольный момент Р единицы объема

и поперечную по отношению к направлению магнитного поля компоненту диэлектрической проницаемости плазмы

В обеих формулах ρm = n( me + mi ) − массовая плотность плазмы.

Расчеты показывают, что величина ε может быть большой, поэтому поле в плазме сильно ослабляется. Например, для дейтериевой плазмы с пара-

123

метрами n=1010см-3, В=103Гс получаем ε ≈102. Если электрическое поле медленно меняется во времени, так что временной масштаб его изменения значительно превышает ларморовский период, то приведенная формула для ε справедлива и в этом случае. Напомним, что формула (2.103) ранее была получена при рассмотрении поляризационного дрейфа.

Диэлектрические свойства плазмы в магнитном поле претерпевают существенное изменение, величины ε|| и ε различны, и

диэлектрическая проницаемость замагниченной плазмы становится тензорной величиной. При этом компонента ε|| остается такой же,

как и в случае плазмы без магнитного поля. Она зависит от частоты падающей волны и плотности числа частиц плазмы, тогда как компонента ε − от массовой плотности плазмы и напряженности

магнитного поля.

• Поперечная проводимость

Картина со свободным дрейфом плазмы в скрещенных полях справедлива лишь при условии, что нет причин, мешающих этому свободному движению плазмы. Реализовать такой случай можно, например, в случае аксиально-симметричного соленоида с дополнительным радиальным электрическим полем. Если ось Z направить вдоль оси соленоида, а ось Y − по радиусу, тогда ось X соответствует вращению по углу ϕ вокруг оси соленоида. Такие системы существуют, и в движущейся плазме удается накапливать весьма заметную энергию - по существу создаются плазменные конденсаторы с большим значением ε . Другое применение − плаз-

менные центрифуги − было рассмотрено ранее.

Если же по направлению дрейфа возникает какое-либо препятствие, то происходит перераспределение плотности частиц, так как вблизи препятствия частицы накапливаются. В результате возникает градиент давления и сила (в расчете на одну частицу) F= −p/n. Эта сила приводит к появлению дополнительного дрейфа, причем электроны и ионы дрейфуют в разные стороны − возникает ток. Таким образом, восстанавливается проводимость поперёк магнитного поля В.

На рис. 2.18 поле В направлено вдоль оси Z, а поле Е - вдоль оси Y и возникает дрейф вдоль оси X. Если имеется какое-либо препятствие, то вблизи него плотность повышается; возникает p и отвечающая ему сила F. Дрейф под действием силы F направлен для ионов вдоль оси Y, для электронов - антипараллельно Y. Появ-

124

ляется ток j, направленный вдоль оси Y, то есть вдоль вектора напряженности электрического поля - проводимость «восстанавливается». Вычисляя этот ток, надо учитывать трение, возникающее при относительном движении электронов и ионов.

Рис.2.18. Схема восстановления проводимости

Точный вывод, строго учитывающий взаимодействие ионов и электронов [13], показывает, что поперечная проводимость не равна продольной, σ ≠σ||, т.е. проводимость плазмы анизотропна. При этом отношение σ /σ|| зависит от зарядового числа иона. Для ионов с Z=1, например, для водородной плазмы

В общем случае ток течет под углом к направлению электрического поля, и закон Ома для плазмы выглядит следующим образом [13]:

Здесь справа выделены все слагаемые, в которые входит плотность тока, в том числе последнее из них отвечает эффекту Холла, а слева в формуле фигурирует эффективное поле, равное

Здесь первое слагаемое − напряженность электрического поля, второе учитывает эффект индукции, возникающий при пересечении потоком плазмы силовых линий магнитного поля, третье связано с градиентом электронного давления, а последнее учитывает влияние термо-ЭДС, возникающей из-за термосилы, в сильно замагниченной плазме примерно равной:

125

Формула (2.105) представляет собой, по существу, одну из возможных форм записи закона Ома для замагниченной плазмы. Из неё следует, что в сильном магнитном поле в направлении вдоль поля соотношение между соответствующей компонентой напряженности электрического поля и плотности электрического тока такое же, как и в отсутствие магнитного поля

||

Поперечная составляющая, однако, претерпевает существенное изменение: эффективное поле оказывается практически перпендикулярным к току. Проекция поперечного поля на ток связана с поперечной компонентой плотности тока соотношением, которое фактически не сильно отличается от предыдущего:

Но для протекания тока поперек магнитного поля нужна составляющая эффективного поля, перпендикулярная и к магнитному полю, и к току - это так называемое холловское поле:

Зачастую холловское поле возникает в плазме автоматически за счет небольшого нарушения квазинейтральности, а внешние поля, которые надо прикладывать к плазме, определяются соотношениями (2.108,а) и (2.108,б). Иногда говорят, что магнитное поле не влияет на проводимость плазмы. Это надо понимать именно в указанном смысле.

• Дрейфовые токи

Всегда, когда возникает градиент давления, появляется и отвечающая ему сила, в расчете на одну частицу (электрон или ион),

причем частицы с зарядами разных знаков дрейфуют в противоположные стороны. Это приводит к переносу заряда, т.е. к проводимости, появлению так называемых токов намагничения или дрейфовых токов

126

Появление электрических токов вследствие неэлектрических причин − специфическая особенность плазмы, присущая ей всегда, когда есть какие-либо неоднородности плазмы.

Из теории магнетизма [15] известно, что намагничение среды I и плот-

Так как движение, перпендикулярное магнитному полю, имеет две степени свободы, то, производя усреднение, и обозначив p =nT , получаем

В этой форме записи учитываются дрейфовые токи, возникающие вследствие градиента плотности и градиента магнитного поля. Если магнитное поле однородно, то формула (2.114) фактически совпадает с (2.111).

127

новения магнитного поля в плазму, то плазму можно рассматривать как идеальный проводник.

Как известно [15], время τs (так называемое скиновое время) проникновения поля на заданную глубину δ в проводнике определяется по формуле

коэффициент магнитной диффузии поля в проводник. Для времен t <<τs плазму можно рассматривать как идеальный проводник с вмороженным в него магнитным полем. Таким образом, одно из условий применимости приближения идеальной гидродинамики к плазме состоит в том, что длительность процесса t должна быть меньше скинового времени τs.

Кроме того, магнитную гидродинамику обычно применяют к описанию плазмы в достаточно сильном магнитном поле и влиянием конечности ларморовского радиуса пренебрегают. Это возможно, если характерный размер области, занятой плазмой, L значительно больше ларморовского радиуса иона. Наконец, необходимо обеспечить квазинейтральность плазмы. Все эти условия можно записать в виде

Zni-ne = 0.

Установив такие ограничения (на самом деле, они более жесткие), можно применить для описания динамики плазмы уравнения магнитной гидродинамики, дополненные уравнениями Максвелла.

Магнитогидродинамическое представление плазмы может быть расширено рассмотрением не однокомпонентной проводящей жидкости, а смеси двух компонент − электронной и ионной. Такое обобщение становится необходимым, когда в плазме протекает ток с заметной плотностью, и уже нельзя считать, что скорости компонент плазмы совпадают, как это принято в одножидкостной гидродинамике. Двухжидкостное рассмотрение расширяет возможности

129

метода, однако, на практике приходится пользоваться и гидродинамическими и кинетическими представлениями совместно, так как гидродинамика не может отразить некоторые существенные стороны процесса.

§ 22. Основные уравнения

Основу любой гидродинамики составляют три закона сохранения − массы, импульса и энергии. При этом основными параметрами, характеризующими движение среды, являются массовая плотность, массовая скорость и давление, зависящие в общем случае от времени и координат. В магнитной гидродинамике, кроме того, вводят плотность электрического тока и вектор индукции магнитного поля. Для их определения уравнения динамики проводящей среды дополняют уравнениями Максвелла.

Введем следующие обозначения:

• плотность массы

ρ = ∑nα mα = ∑ni mi ,

здесь α − индекс сорта частиц (электроны, ионы). Так как масса иона значительно превосходит массу электрона, Mi>>me то вкладом массы электронов в плотность ρ обычно пренебрегают;

• массовая скорость

по той же причине примерно равна скорости ионной компоненты;

• плотность заряда

ρq = ∑nα qα =| e | (Zni − ne ) ,

(α)

где |e| − абсолютная величина заряда электрона;

• плотность тока rj = ∑nα qα vrα .

( α )

Если предполагается, что скорость электронов ve значительно превосходит скорость ионов vi, то

130