
Жданов Основы физических процессов 2007
.pdf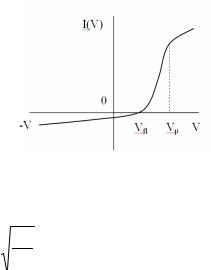
Если учесть возможную эмиссию электронов из поверхности с коэффициентом δ<1, то из баланса токов следует, что выражение под знаком логарифма в (1.9) следует разделить на (1-δ)2.
Ленгмюровский зонд
Введение в плазму металлического зонда позволяет опреде-
лить ее параметры по вольт-амперной характеристике (ВАХ) (рис.1.3). При максвелловском распределении электронов по скоростям и выполнении условия бесстолкновительности такой зонд называют зондом Ленгмюра, и это самый распространенный метод измерения параметров плазмы, особенно низкотемпературной при
Te>>Ti. Левая часть ВАХ соответствует отрицательному потенциалу на зонде, электроны плазмы заперты этим потенциалом, а ионный
ток насыщения при |
|
V |
|
>> Te / e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Рис.1.3. Вольт-амперная ха- |
|
|||||||||
определяется скоростью |
ионов |
|
|
||||||||
(1.11) и для цилиндрического зон- |
|
рактеристика (ВАХ) зонда |
|
||||||||
да связан с температурой и кон- |
|
Ленгмюра |
|
|
|||||||
центрацией плазмы соотношением: |
Te S |
|
|
|
|
||||||
i ≈ 0,56n e |
c |
, |
(1.14) |
||||||||
i |
e |
Mi |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
где Sc − площадь собирающей поверхности зонда.
Следует иметь в виду, что площадь поверхности, собирающей ускоренные по направлению к зонду ионы, может не совпадать с материальной поверхностью зонда и быть больше ее. В этом случае используют поправочные функции, которые зависят от соотношений между радиусом зонда, радиусом Дебая и между ускоряющим потенциалом и температурой электронов [38].
Ток электронов в тормозящем поле определяется из (1.10). Поэтому в той части ВАХ зонда, где выражение (1.10) применимо, температура плазмы связана с током электронов на зонд ie соотношением:
21
Te = − |
|
e |
|
. |
(1.15) |
d(ln i |
) |
||||
|
|
e |
|
|
|
|
|
dV |
|
|
|
При больших положительных потенциалах на зонде ионный ток отсутствует, и ток на зонд определяется электронным током насыщения. В точке выхода на насыщение (Up) электронного тока его значение позволяет найти концентрацию электронов:
n = |
4ie (Vp ) |
. |
(1.16) |
|
|||
e |
eveSз |
|
|
|
|
||
Таким образом, из зондовой характеристики можно определить концентрацию и электронную температуру плазмы. Следует при этом иметь ввиду, что условие отсутствия экранировки зондом других областей плазмы прдполагает, что его размер rз должен быть много меньше средней длины свободного пробега частиц в плазме λ, что вместе с условием бесстолкновительности дебаевского слоя соответствует условию
λ>>rз+rD.
§ 3. Идеальность плазмы
По аналогии с газом плазму считают идеальной, если средняя кинетическая энергия частиц существенно больше потенциальной энергии их взаимодействия. В газе потенциальная энергия взаимодействие частиц обусловлена силами Ван-дер-Ваальса, в плазме − кулоновским взаимодействием. Энергия кулоновского взаимодействия двух частиц с зарядом е, находящихся на расстоянии R друг от друга, равна e2/R. Среднее расстояние между частицами при плотности плазмы n составляет R n−1/3, а средняя кинетическая энергия частицы по порядку величины равна температуре T, измеряемой в энергетических единицах.
Таким образом, условие идеальности плазмы можно сформулировать следующим образом:
e2 n1/ 3 << T ,
или
22
γ = |
e2n1/ 3 |
<<1, |
(1.17) |
|
T |
||||
|
|
|
где γ − параметр неидеальности. Этому условию можно придать и несколько иной смысл. Сечение кулоновского взаимодействия частиц определяется амплитудой рассеяния по порядку величины равной
f ~ |
e2 |
. |
|
T |
|||
|
|
Очевидно, плазма является идеальной, если амплитуда рассеяния значительно меньше среднего межчастичного расстояния (в противном случае существенны корреляции взаимного расположения частиц)
f<< R ~ n−1/ 3 ,
имы вновь приходим к критерию (1.6).
Полезно условию идеальности плазмы придать более наглядный смысл, а именно, выделить в объеме плазмы сферу с радиусом равным радиусу Дебая и подсчитать число частиц ND, содержащихся в этой сфере:
N |
D |
= |
4 |
πnr 3 |
~ γ −3/ 2 . |
(1.18) |
|
||||||
|
|
3 |
D |
|
|
|
|
|
|
|
|
|
Сравнив с критерием (1.6), приходим к заключению, что плазма является идеальной, если число частиц в сфере с дебаевским радиусом велико. Часто именно число ND используется в качестве меры идеальности или неидеальности плазмы.
Проиллюстрируем полученный результат численным примером. Так, для значений температуры и плотности, типичных для термоядерной плазмы (см. §2), получаем ND~103>>1, и такая плазма является в высокой степени идеальной. Тогда как для плазмы молнии, типичная температура которой составляет ~104К, а концентрация примерно равна концентрации воздуха, ~1019см-3, получаем ND~0.1. Такая плазма является слабонеидеальной, способной, тем самым, к рождению самоподдерживающихся нелинейных структур. Возможно, как полагают, именно такова природа шаровой молнии, возникающей часто при обычном грозовом разряде. Впрочем, детальный механизм этого природного явления пока окончательно не выяснен.
Понятие идеальности применимо и к вырожденной плазме. Однако в этом случае энергию кулоновского взаимодействия частиц сравнивают с энергией Ферми Ef . Как известно, применимость
23
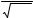
классического или же квантового описания частиц и их взаимодействия определяется отношением длины волны де-Бройля λБ к характерному расстоянию, в качестве которого удобно взять n-1/3. При λБ<< n-1/3 мы имеем дело с классическим описанием, при λБ≥ n- 1/3 с квантовым. Представляя средний импульс частицы в среде как
p~(mT)1/2, для критерия вырождения имеем λБ ~ |
h ≥ n-1/3 или |
||||||||||
|
|
|
|
|
|
|
|
|
|
mT |
|
T ≤ |
|
h2n2/ 3 |
~ E f . |
(1.19) |
|||||||
|
|
m |
|||||||||
|
|
|
|
|
|
|
|
||||
Условие идеальности вырожденной плазмы будет соответст- |
|||||||||||
вовать выполнению соотношения e2n-1/3 << (h2n2 / 3 ) / m или |
|||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
2 |
|
|
3 |
|
1 |
|
|
||
n >> |
e |
me |
|
= |
, |
(1.20) |
|||||
|
|||||||||||
|
|
h |
2 |
|
3 |
|
|
||||
|
|
|
|
|
aБ |
|
|||||
где aБ – радиус Бора (aБ=0,529 10-8см). Энергия кулоновского взаимодействия на этом расстоянии в расчете на одну частицу равна e2/2aБ ≡ RY (энергия Ридберга RY=13,6 эВ).
На рис.1.4 в координатах температуры и концентрации показаны области, для которых выполняются приведенные выше соотношения. Там же обозначены области значений n и T, характерных для различных плазменных объектов.
§ 4. Элементарные процессы в плазме
Элементарные процессы – это столкновения атомных частиц (электронов, ионов, атомов, молекул), а также изменение их состояния в результате поглощения или излучения электромагнитного излучения.
Элементарные процессы в плазмы делятся на прямые и обратные, см. таб. 1.1, в которой смысл процессов проиллюстрирован их упрощенными схемами переходов между уровнями энергии. Первый прямой процесс связан с переходом электрона на возбужденный уровень под действием кванта излучения или при соударении, а обратный с релаксацией этого возбуждения, сопровождающегося испусканием фотона.
24
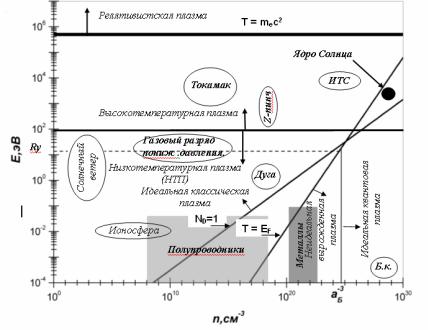
Рис.1.4. Виды плазм. ND=1 – число частиц в сфере Дебая, T=EF , где EF – энергия Ферми – критерий вырожденности плазмы. ИТС – инерционный термоядерный синтез, Б.к. – белые карлики
Диссоциация сопровождается переходом электрона на анитисвязанное состояние атомов в молекуле, а третий процесс – это переход электрона в область непрерывного спектра положительных энергий, обратный ему процесс сопровождается высвечиванием кванта или передачей энергии другому электрону в оже-процессе.
Столкновения бывают парные, тройные или многочастичные.
Парные соударения преобладают в разреженной плазме, когда когда влиянием окружающих частиц на соударение между двумя частицами можно пренебречь. Вероятность тройных соударений растет ~ n3, поэтому они могут играть роль в более плотной плазме,
а многочастичные соударения могут происходить, например, при взаимодействии частиц плазмы с конденсированной средой (твердым телом или жидкостью).
25
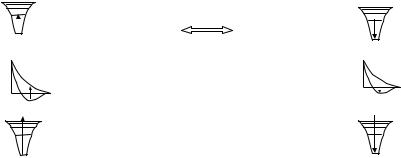
Таблица 1.1.
прямые обратные
возбуждение тушение
диссоциация  ассоциация
ассоциация
ионизация  рекомбинация
рекомбинация
Столкновения частиц делят на упругие, которые происходят без изменения внутренней энергии или состояния сталкивающихся частиц, и неупругие, приводящие к такому изменению. Первые отвечают за распределение частиц в плазме по энергии, а вторые за распределение частиц по внутренним степеням свободы или по их сортам. Среди неупругих соударений могут быть и такие, которые происходят без (или почти без) изменения внутренней энергии частиц. Такие соударения называют резонансными или квазирезонанс-
ными.
В общем случае оценку вероятности процесса возбуждения электронов атома, молекулы или иона можно получить, сравнивая время взаимодействия частиц и время соответствующего перехода. Атомные частицы взаимодействуют своими электронными оболочками, и если сближение происходит медленно (т.е. относительные скорости атомных частиц малы по сравнению со скоростью электронов в атоме), то их электронные оболочки успевают постепенно перестроиться, а затем вернуться в исходное состояние. Если же время взаимодействия мало, то электроны за время tэ "перебрасываются" на новый уровень, происходит возбуждение. Таким образом, возбуждение не происходит, если tат>>tэ. По порядку величины tат= a/v, где a − размер атома, a v − относительная скорость. Порядок величины tэ можно определить из принципа неопределенности:
t = h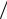 δE,
δE,
26
где δE − разность энергий уровней. Поэтому получаем условие
a / v >>h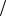 δE
δE
или
aδE / vh >>1 , |
(1.21) |
что и является критерием маловероятности перехода и называется
адиабатическим критерием Месси. Очевидно, что если разность энергий уровней δЕ мала, то процесс более вероятен, что и соответствует резонансному процессу.
Иногда соударения делят по отношению взаимной скорости сталкивающихся частиц к скорости электрона на первой боровской орбите:
vБ = e2 / h = 2,2 108 см/c. |
(1.22) |
При v << vБ столкновения медленные, при v ≥ vБ столкновения быстрые.
Вероятность соударения частиц определяют их сечением взаимодействия σ. Для упругих столкновений медленных атомов или молекул, в первом приближении сечения имеют порядок квадрата поперечного размера частиц, например, как известно, размер атома водорода определяется радиусом Бора аB=0.529·10-8 см, так что сечения упругих столкновений составляют σ упр~10-16 см2. Для соударений, при которых происходят ядерные реакции, например, реакции синтеза легких элементов сечение определяется характерным размером ядра (~ 10-12 см2), поэтому сечения ядерных соударений измеряют в барнах (один барн равен 10-24см2). Так, для реакции синтеза дейтерия и трития:
D + T = 4He + n +17,59 МэВ, |
(1.23) |
имеющей наибольшее сечение из реакций всех других легких элементов, максимальное значение сечения при энергии ~ 100 кэВ составляет один барн.
27
§ 5. Упругие соударения
Динамика rпарных упругих соударений частиц (массой Мi и координатой ri ) определяется потенциальной энергией
межчастичного взаимодействия W в соответствии с уравнением движения
|
M |
|
d 2r |
r |
r |
|
|
i |
= F . |
F = − W . |
|
|
|
i |
dt2 |
i |
i |
При этом |
используют |
различные |
потенциалы взаимодействия |
||
U = W/e. |
Очевидно, что |
при соударении несжимаемых тел |
|||
(например твердых шаров диаметра a) потенциал имеет ступенчатый характер U(r) = 0 при r ≥ a и U(r) = ∞ при r < 0. При этом полное сечение взаимодействия σ=πa2. Наиболее короткодействиющим является потенциал твердых сфер, а наиболее дальнодествующим – кулоновский потенциал. Все остальные потенциалы можно представлять в виде степенных потенциалов вида U 1/rn , где n меняется от единицы до бесконечности, или в виде экранированных кулоновских
потенциалов вида (1.6) |
или их комбинаций. |
В случае |
центрально симметричного потенциала |
межчастичного взаимодействия траектория частицы определяется прицельным парметром ρ и относительной скоростью частиц.
Дифференциальное сечение упругого рассеяния dσ = 2πρdρ.
Представляет интерес оценить энергию, которой должна обладать частица для того, чтобы произошла реакция синтеза (1.24). При нулевом прицельном параметре расстоянию наибольшего сближения ионов дейтерия и трития будет сответствовать равенство кинетической энергии налетеющей частицы и потенциальной энергии их кулоновского расталкивания E =e2/rяд. Полагая rяд=10-12см, получим E≈144 кэВ, что близко к энергии, соответсвующей максимуму сечения этой реакции.
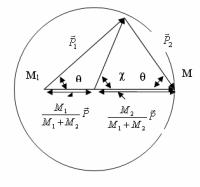
При упругих соударениях любых тел, в том числе и атомных частиц, законы сохранения энергии и импульса приводят к хорошо известному из общей физики распределению сталкивающихся частиц по энергиям в зависимости от угла рассеяния (рис.1.5). Для обсуждения процессов в плазме крайне важно выражение для переданной в упругом соударении энергии, которое для первоначально
28
покоившейся частицы соответствует приобретенной ею энергии после соударения:
E2 = E0 |
4M1M2 |
2 |
θ2 . |
(1.24) |
|
cos |
|||
(M1 + M2 )2 |
Из уравнения (1.24) следует, что максимальная переданная в упругом столкновении энергия не может превышать 4М1М2/(М1+М2)2 от первичной энергии частицы. При соударениях ионов (атомов) и электронов переданная энергия составляет малую величину, определяемую отношением
me/Mi.
|
|
|
При |
соударениях |
ней- |
||||
|
|
|
тральных |
атомов |
и |
молекул |
|||
|
|
|
следует учитывать возможность |
||||||
|
|
|
их взаимной |
поляризации на |
|||||
Рис.1.5. |
Диаграмма |
упругого |
малых |
|
расстояниях. |
||||
Поляризованные атомы |
или |
||||||||
рассеяния частиц. |
Частица |
молекулы притягиваются полем, |
|||||||
массой М2 первоначально по- |
потенциал |
которого |
изменяется |
||||||
коилась, |
а частица массой М1 |
||||||||
имела импульс P . Импульсы |
как U 1/r6. При дальнейшем |
||||||||
сближении |
|
электронные |
|||||||
частиц |
после соударения |
оболочки |
взаимодействующих |
||||||
P1 и P2 , |
χ − угол рассеяния в |
||||||||
частиц взаимно проникают друг |
|||||||||
системе центра инерции, θ1 – |
в друга, а силы молекулярного |
||||||||
угол рассеяния частицы М1, θ2 |
притяжения |
переходят |
в |
силы |
|||||
− угол вылета частицы М2 в |
отталкивания. |
Определение |
|||||||
лабораторной системе |
|
зависимости |
этих |
|
сил |
от |
|||
|
|
|
межчастичного |
|
расстояния |
||||
|
|
|
представляет |
собой |
|
сложную |
|||
квантово-механическую задачу. На практике для их описания используют полуэмпирические аппроксимации, учитывающие резкую зависимость сил отталкивания от расстояния с помощью обратностепенной или экспоненциальной функции. Часто используют, на-
29

пример, потенциал Леннарда-Джонса, в котором соответствующая отталкиванию часть описывается функцией U 1/r12. Результирующий потенциал взаимодействия при этом:
|
|
|
|
12 |
r |
6 |
|
|
||
U = 4U |
|
r |
|
|
|
|
||||
min |
|
m |
|
− |
m |
|
|
|
(1.25) |
|
r |
|
|
||||||||
|
|
|
|
r |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет вид кривой с минимумом (рис.1.6).
U(r)
U 1/r12
0
Umin
rmin
U 1/r6
Рис.1.6. Потенциал взаимодействия между двумя медленными атомами
В первом приближении заряженные частицы взаимодействуют с нейтральными также, как и нейтральные частицы между собой. Заряженная час-тица своим полем поляризует нейтральную, и сечение рас-сеяния
rопределяется не только геометрическими размерами нейтральной частицы, но и ее поляризуемостью. Особенно большой поляризуемостью обладают щелочные металлы
и некоторые атомы в возбужденном состоянии. Поляризуемость молекул существенно ниже, она близка к поляризуемости нещелочных атомов.
Сечения упругих столкновений медленных электронов с атомами порядка квадрата размера атома. Следует иметь в виду, что для медленных электронов с энергиями в несколько электрон-вольт длина волны де-Бройля
D = h/ p |
(1.26) |
больше размеров атома, поэтому описание взаимодействия возможно только квантовомеханическое. Дифференциальное сечение рассеяния в этом случае представляется в виде
dσ = f(θ) 2dθ,
где f(θ) – амплитуда рассеяния на угол θ.
Упругие столкновения заряженных частиц имеют иной характер, и в сильноионизованной плазме именно они определяют форму функций распределения и процессы переноса. Рассмотрим по-
30
