
Жданов Основы физических процессов 2007
.pdfА* + В → АВ+ + е - ассоциативная ионизация сопровожда-
ется образованием молекулярного иона, А* + В → А + В+ + е - процесс Пеннинга происходит, если энергия возбуждения атома А* в метастабильное состояние больше потенциа-
ла ионизации частицы В.
Фотоионизация
A + hν =A++e
происходит, если энергия кванта больше энергии ионизации, что для длины волны излучения соответствует формуле:
λ[см] = 1,23 10−6 . I[эВ]
Сечение фотоионизации примерно на два порядка меньше, чем при ионизации электронным ударом, оно максимально при энергии квантов вблизи порога и резко падает с увеличением длины волны. Для атома водорода и квантов с энергией, много боль-
шей энергии ионизации σhν [см2 ] ≈ 23,8λ7.2 . Возбуждение фото-
нами имеет четкий резонансный характер для атомов и атомарных ионов и более "размыто" для молекул.
Диссоциацией называют процесс разделения сложных молекул (или молекулярных ионов) на более простые молекулы, или на атомы (или ион и атом, ион и молекула). Энергия разрыва молекулярных связей почти всегда меньше энергии ионизации (за исключением, пожалуй, молекул СО2 и С2Н2). Часто диссоциацию облегчает накопление энергии на колебательно-вращательных уровнях молекулы. Диссоциация молекул и молекулярных ионов возможна за счет множества различных процессов, при которых молекуле передается энергия больше энергии диссоциации. Например, при столкновении молекул между собой возможны различные процессы распада:
АВ + СD → А + В + СD,
АВ + CD → АВ +С+D, АВ + СD → А + В + С + D.
41
При электронном ударе сечения диссоциации ведут себя так же как и сечения других неупругих процессов под действием электронов.
Образующиеся при диссоциации атомы называются франккондоновскими по названию
принципа Франка-Кондона,
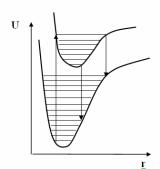
согласно которому переходы между энергетическими уровнями молекулы (термами) (рис.1.12) происходят очень бысто по сравнению с движением ядер. Так как при таком быстом переходе расстояния между ядрами не успевают измениться, то франккондоновский переход можно изобразить вертикальной линией
между соответсвующими энергетическими уровнями. Причем эти переходы происходят в точках пересечения колебательных уровней (изображены на рис.1.13 горизонтальными прямыми) с электронными термами. Квазиклассическое объяснение состоит в том, что в этих точках «поворота» колеблющиеся ядра атомов находятся наиболее долго.
Девозбуждение, рекомбинация
Возбужденные атомы и молекулы не могут долго оставаться в таком состоянии, поскольку возбужденные состояния имеют вполне определенное конечное время жизни τ, спустя которое происходит переход в основное состояние, сопровождающийся излучением кванта. В большинстве случаев τ=10-7 -10-8с, однако существуют и метастабильные состояния, время жизни в которых существенно выше τ =10-1-10-4с и зависит от свойств и концентрации.
Снятие электронного возбуждения возможно многими путями, например:
а) А* → А + hν - высвечивание при возвращении электрона на основной уровень (возможно
42
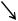
ступенчатое путем испускания ряда фотонов);
б) А* + ВС → А + ВС - тушение при столкновении с молекулой, энергия возбуждения переходит или в кинетическую энергию частиц, или расходуется на диссоциацию молекулы (тушение при соударении с атомом маловероятно);
в) А* + В → В* + А - передача возбуждения реализуется с большой вероятностью, если мало изменение энергии перехода (резонансный процесс);
г) AZ+1+e→(AZ)**→AZ +hν- диэлектронная рекомбинация
автоионизационного состояния возбужденного иона с зарядом Z;
д) AZ+1+e→(AZ)**→AZ + e - автоионизационный распад того же состояния за счет эффекта Оже.
Эффект Оже состоит в передаче энергии электрона, переходящего на более низкий энергетический уровень, другому электрону. Процессом, обратным ионизации, является объединение иона и электрона - образование нейтральной частицы или понижение зарядности иона, его называют рекомбинацией. При рекомбинации выделяется энергия, равная энергии связи рекомбинирующих частиц. Эта энергия может выделиться в виде излучения, или может быть передана третьей частице (обычно одному из электронов плазмы). В первом случае говорят о фоторекомбинации, во втором – о тройной рекомбинации. Очевидно, что второй случай реализуется при высоких плотностях плазмы.
Иногда рекомбинацией называют и ассоциацию молекул из атомов, т.е. процессы типа А + 2В → АВ + В, А + В + С → АВ + С,
или А + 2А → А2 + А.
Перезарядка. Весьма важным является процесс передачи заряда от заряженной частицы к нейтральной:
А+ + В ↔ А + В+.
В случае тождественных частиц А и В (кроме зарядового состояния) процесс носит резонансный характер и обладает очень большим сечением, значительно большим, чем сечение ионизации.
43
Если потенциал ионизации нейтральной частицы больше потенциала ионизации заряженной частицы, то на величину энергии, соответствующую этой разнице, уменьшится полная кинетическая энергия частиц. В случае, если энергия ионизации заряженной частицы больше энергии ионизации нейтральной частицы, то избыток энергии выделится или в виде кинетической энергии частиц, или пойдет на возбуждение (у атомов последнее бывает редко).
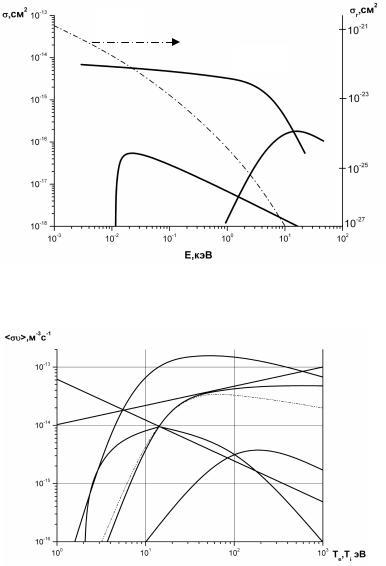
Наиболее важные для описания плазмы в термоядерных установках сечения неупругих процессов с участием атомарного водорода приведены на рис.1.14. Так как все неупругие процессы зависят от относительной скорости частиц, то в плазме существенную роль играют скорости соответсвующих процессов <σv>. Треугольные скобки означают, что произведено усреднение по максвелловскому распределению частиц по скоростям. На рис.1.15 показана зависимость скорости основных неупругих процессов в водородной плазме от ее температуры.
Излучательные процессы
Многие из вышеупомянутых неупругих процессов сопровождаются излучением квантов электромагнитного излученя. Не останавливаясь на релаксации колебательных и вращательных возбуждений в плазме с участием молекул, подчеркнем, что релаксация или девозбуждение электронных уровней сопровождается линейчатым излучением. Напомним, что энергия излучаемых квантов при девозбуждении атома водорода выражается известной формулой
|
1 |
|
1 |
|
|
|
|
|
|
|
|||
|
− n2 |
, |
(1.39) |
|||
hν = Ry n2 |
|
|||||
|
i |
|
k |
|
|
|
где Ry=13,6 эВ – энергия Ридберга, ni |
= 1,2,3,4 …, nk = ni+1, ni+2, |
|||
ni+3...... |
ni=1 |
соответствует серия |
Лаймана, |
ni=2 – серия |
Бальмера, |
ni=3 |
– серия Пашена, |
ni=4 – |
серия Брэкета. |
Спектральные линии серии Лаймана обозначаются Lα, Lβ, Lγ, где буквы греческого алфавита соответсвуют переходам с уровней nk=2,3,4 и т.д. Аналогично, для серии Бальмера принято обозначение Hα, Hβ, Hγ и т.д. С ростом температуры плазмы интенсивность линейчатого излучения падает (до тех пор, пока
44
не начинает возбуждаться более глубокая электронная оболочка атома, см. рис. 9.9).
σrec
σcx
|
|
σii |
e |
||
σi |
|
|
|
|
Рис.1.14. Энергетическая зависимость основных сечений неупругих процессов для атомарного водорода: σie – сечение ионизации электронным ударом, σii – сечение ионизации ионным ударом, σcx – сечение резонансной перезарядки, σrec – сечение фоторекомбинации.
Рис.1.15. Скорости основных неупругих процессов для водорода
45
При температуре Te > 1 кэВ интенсивность линейчатого излучения атомов с Z≈10
Pлин. nine |
Z |
6 |
. |
(1.40) |
|
T 3 / 2 |
|||||
|
|
|
|||
|
e |
|
|
|
|
Фоторекобинация электрона из области непрерывных уровней дает сплошной спектр. В ходе диэлектронной рекомбинации электрон остова переходит на основной уровень, а ион меньшей кратности остается возбужденным. Спектр излучения представляет собой суперпозицию сплошного и линейчатого. Мощность энергии, уносимой рекомбинационным излучением,
Pлин. nine |
Z |
4 |
. |
(1.41) |
|
T1/ 2 |
|||||
|
|
|
|||
|
e |
|
|
|
|
При большей температуре, когда электроны свободные, они могут излучать в процессе их торможения на ионах (свободносвободные столкновения). Так как мощность излучения при торможении заряженной частицы пропорциональна квадрату ускорения, то при кулоновском взаимодействии
Pторм |
|
r |
|
2 |
= (e2Z / m )2 |
|
|
||||
|
&r& |
|
|
||
|
|
|
|
|
e |
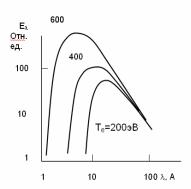
(из за большой массы излучение ионов при торможении пренебрежимо мало). Спектр тормозного излучения непрерывный (рис.1.16) с коротковолновой границей, соответствующей энергии
электрона, и максимумом при: λ(A) ≈ 6200 / Te [эВ]. (Энергия и
длина волны кванта в ангстремах связаны соотношением E[эВ]=12395/λ[Å]. Мощность тормозного излучения растет с температурой
Pторм=Kторм nineZ2Te1/2. |
(1.42) |
Если удельную мощность измерять в (Вт/м3 ), концентрацию в
(м- 3 ), а температуру в (эВ), то Кторм = 1.7 10- 3 8 . Таким образом, если линейчатое (1.40) и рекомбинационное (1.41) излучение быст-
ро падает с ростом температуры, то тормозное излучение становит46
Pцикл |
|
r |
|
2 |
= (v2 / ρ |
)2 |
T H 2 . |
|
|
||||||
|
&r& |
|
|
||||
|
|
|
|
|
l |
|
e |
В главе 9 при обсуждении энергетического баланса высокотемпературной плазмы на рис.9.9 показана зависимость радиационных потерь для различных элементов. Если для водорода при температурах выше ~ 100 эВ доминирует тормозное излучение, то для тяжелых элементов потери энергии определяются линейчатым излучением атомных остовов неполностью ионизованных атомов, их излучением за счет фото- и диэлектронной рекомбинации.
§ 7. Равновесия в плазме
При полном термодинамическом равновесии должно устано-
виться равенство скоростей всех прямых и обратных процессов, а также равенство всех температур (вращательных, колебательных, электронной, ионной, атомной). Такую сложную схему рассмотреть крайне трудно, а может быть и невозможно. Часто говорят о частичных равновесиях – при малых температурах по всем степеням свободы (кинетической энергии электронов и ионов, колеба-
47

тельным, вращательным состояниям), при больших, когда молекул и атомов уже практически нет, – о температурах хаотического движения электронов и ионов.
Рассмотрим примеры ионизационного равновесия в атомарном газе (не рассматриваем молекулы, так как это резко усложняет задачу – надо рассматривать колебательно-возбужденные состояния, ассоциативную ионизацию и т.д.; не рассматриваем также и автоионизационные состояния). Простейшими и одновременно наиболее часто встречающимися являются следующие три случая.
Баланс между ионизацией электронным ударом и тройной рекомбинацией
Процесс |
(прямой/обратный) |
Скорость процесса |
a+e→i+2e (ионизация) |
wi = kinane |
|
i+2e→a+e |
(рекомбинация) |
wp = kpnine2 |
Здесь na, ni, ne – плотности атомов, ионов и электронов соответственно; ki, kp – коэффициенты скорости ионизации и рекомбинации. Скорость производства, например, ионной компоненты в таких процессах определяется уравнением:
dndti = wi − wp .
В равновесии скорости прямого и обратного процессов совпадают, так что должно быть wi = wp, и константа равновесия K, которая определяется как отношение коэффициентов скоростей прямых и обратных процессов, оказывается равной:
K = |
ki |
= |
ne ni |
. |
kp |
|
|||
|
|
na |
||
Заметим, что введенная таким образом константа равновесия имеет размерность куба обратной длины.
Баланс между фотоионизацией и фоторекомбинацией
Процесс (прямой/обратный) |
Скорость процесса |
|
a+γ→i+e (ионизация) |
′ |
′ |
|
wi |
= kina j |
48
i+e→a+γ (рекомбинация) |
′ |
′ |
|
wp = kpnine |
|
Здесь na, ni, ne - плотности атомов, ионов и электронов соответственно, ki′j, kp′ - коэффициенты скорости фотоионизации и фоторе-
комбинации.
В равновесии
wi′ = w′p ,
и константа равновесия, определяемая так же как и в предыдущем случае, оказывается равной
K = |
ki′j |
= |
ni ne |
|
k ′ |
|
|||
|
|
n |
a |
|
|
p |
|
|
|
(по принципу детального равновесия), так что в обоих случаях
K = |
ni ne |
. |
(1.43) |
|
|||
|
na |
|
|
Баланс между ионизацией электронным ударом и фоторекомбинацией
В предыдущем примере предполагается, что излучение заперто и не выходит из реакционного объема. Если же плазма прозрачна для излучения, т.е. её плотность достаточно мала, то мала скорость фотоионизации, и ионизация обусловлена главным образом соударениями. В плазме малой плотности маловероятны и тройные соударения, поэтому главным конкурирующим процессом является рекомбинация с излучением:
Процесс (прямой/обратный) |
Скорость процесса |
||
a+e→i+2e |
(ионизация) |
′ |
= kinane |
|
|
wi |
|
i+e→a+γ |
(рекомбинация) |
′ |
′ |
|
|
wp = kpnine |
|
Приравнивая скорости прямого и обратного процессов, полу-
чим формулу Эльверта:
49
K′ = |
ni |
= |
ki |
|
|
|
|
. |
(1.44) |
||
na |
k′p |
||||
Степень ионизации
Степень ионизации определяют как отношение числа ионов к полному числу частиц n0.
α = |
|
ni |
= |
ni |
. |
(1.45) |
n |
+ n |
|
||||
|
|
n |
|
|||
|
i |
a |
0 |
|
|
|
В случае применимости формулы Эльверта из (1.44) следует, что степень ионизации в этом случае
α = |
|
|
K |
′ |
|
|
|
|
|||
1 |
+ K′ |
||||
|
|||||
не зависит от плотности и является функцией только от температуры, так как от температуры зависит константа равновесия.
В общем случае связь между степенью ионизации и константой равновесия может быть определена следующим образом. Из формулы (1.45) следует, что
ni |
= |
|
α |
. |
n |
|
|||
|
1−α |
|||
a |
|
|
|
|
В то же время из условия квазинейтральности и определения K (1.43) имеем ni2 /na = K, откуда:
α2 |
= |
K |
. |
(1.46) |
|
1−α |
n |
||||
|
|
|
|||
|
|
0 |
|
|
Для плазмы, находящейся в термодинамическом равновесии, константа равновесия К может быть получена как по аналогии с константой химического равновесия, так и из кинетических соображений [2], и оказывается равной:
K = |
n n |
= |
g |
g |
e |
μT |
3 / 2 |
e |
− |
I / T , |
|
||
e i |
i |
|
|
|
|
|
|
(1.47) |
|||||
g |
|
|
2πh2 |
|
|||||||||
|
n |
|
a |
|
|
|
|
|
|
|
|||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
50
