Жданов Основы физических процессов 2007

плазменный шнур окружают массивным медным кожухом). При быстром изгибе токового канала магнитное поле за счет скинэффекта не успевает проникнуть в проводящий кожух, и силовые линии магнитного поля тока оказываются «зажаты» между стенкой и плазмой (см. рис. 4.20,д.). Ввиду сохранения потока, в этой области магнитное поле станет больше, чем на диаметрально противоположной стороне токового канала, и возникает сила, стремящаяся восстановить равновесие. Поскольку механизм стабилизации существенно связан со временем скинирования, медленный изгиб, очевидно, стабилизироваться не может. В этом случае более эффективно управлять положением токового шнура с помощью дополнительных проводников с током, располагаемых на периферии плазмы.

• Винтовая неустойчивость. Критерий Шафранова - Крускала Возникновения змеек можно было бы избежать, если снаружи

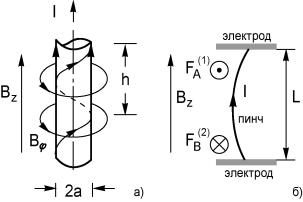
окружить пинч продольным магнитным полем. Но ситуация здесь не такая однозначная, как может показаться на первый взгляд. Внешнее магнитное поле складывается с магнитным полем тока пинча, и образуется конфигурация с винтовыми силовыми линиями (рис. 4.21,а). При изгибе токового канала действующие на разные его участки силы Ампера со стороны внешнего поля «скручивают» плазменный шнур, как это показано на рис. 4.21,б, и шнур стремится завиться в винт. Это и определило название обсуждаемой неустойчивости. Сила Ампера, действующая на ток в магнитном поле, исчезает, когда ток параллелен силовой линии. Именно такое положение и стремится занять токовый шнур, завиваясь в винт. Нетрудно подсчитать шаг винтовой силовой линии. Так как длина окружности в сечении шнура радиуса а составляет 2πа, а при однократном обходе вокруг шнура смещение равно шагу силовой линии h, то, умножив длину окружности на соответствующий угловой коэффициент, получаем

Если учесть, что концы шнура «вморожены» в хорошо проводящие электроды, как это показано на рис. 4.21,б, то в промежутке длины L не уложится ни одного шага винта, а, значит,

201

винтовая неустойчивость развиваться не сможет, если выполнено условие

Это и есть критерий устойчивости относительно развития винтовых возмущений. Мы видим, что для подавления винтовой неустойчивости продольное поле в соответствии с этим критерием должно быть достаточно сильным. Слабое продольное поле только ухудшает ситуацию в плане устойчивости, так как условие (4.90) может нарушаться.

Для систем с замкнутым плазменным шнуром, как это имеет место в тороидальной магнитной ловушке, например в токамаке (см. Главу 9), роль длины системы выполняет длина самого замкнутого шнура. Если его большой радиус равен R (см. рис. 2.6), то, подставив в (4.90) в качестве длины L длину окружности большого радиуса 2πR, получим критерий устойчивости Шафранова – Крускала [23]:

где q – так называемый коэффициент запаса устойчивости.

Рис. 4.21. Винтовая неустойчивость

202

Применительно к токамакам, продольное поле Bz принято называть тороидальным, а поле тока Bϕ − полоидальным. Согласно критерию Шафранова – Крускала тороидальное поле должно быть очень большим, если диаметр сечения шнура значительно меньше его длины по большому радиусу. В этом случае, оценивая величину полоидального поля тока плазменного шнура как

2I Bϕ = ca ,

можем записать критерий устойчивости как условие, ограничивающее допустимый ток в токамаке:

Это условие определяет одну из границ рабочей области для такой системы (так называемый предел по току, см.рис.9.3).

Подчеркнем в заключение, что критерий Шафранова – Крускала является критерием глобальной устойчивости, т.е. устойчивости плазменного шнура в целом, и не гарантирует локальной устойчивости. Например, один из критериев локальной устойчивости (критерий Сайдема) записывается в виде

Здесь последнее слагаемое – шир (или перекрещенность) силовых линий всегда оказывает стабилизирующее действие. Так как в поперечном сечении шнура давление плазмы p(r) по мере удаления от центра убывает, то для устойчивости, при малом шире, должно быть q>1 в соответствии с критерием Шафранова – Крускала. Если окажется так, что на периферии плазменного шнура будет q(a)>1, то глобально шнур будет устойчив. Но если при этом в центре шнура окажется q(0)<1, то возможно развитие внутренней винтовой моды, вызывающей «выворачивание» шнура «наизнанку» и появление пилообразных колебаний его температуры, вследствие перемешивания горячей центральной и холодной периферийной плазмы шнура.

203

§37. Кинетические неустойчивости плазмы

•Механизм обратного поглощения Ландау

Кинетические эффекты становятся существенными, когда фазовая скорость волн оказывается порядка характерной скорости частиц плазмы. Одно из проявлений этих эффектов – бесстолкновительное затухание Ландау, приводящее к затуханию волн в максвелловской плазме. Наличие (или отсутствие) бесстолкновительного затухания определяется знаком производной по скорости от функции распределения в резонансной точке, задаваемой условием черенковского резонанса

ω − kvr = 0 ,

или, другими словами, затухание определяется соотношением количества частиц, скорость которых выше или ниже фазовой скорости волны. Если последних больше, то энергия волны поглощается (§ 33). При наличии в плазме интенсивного пучка частиц (см. рис. 4.22, «горб» на этом рисунке отвечает превышению числа частиц с соответствующей скоростью в пучке над числом частиц, соответствующих максвелловскому распределению), затухание резонансной волны может смениться раскачкой. В этом случае говорят об обратном механизме поглощения Ландау. Если скорость частиц пучка достаточно большая, то частоты резонансных волн будут велики, а длины волн – малы. В этом отношении такие неустойчивости, в отличие от МГДнеустойчивостей, преимущественно мелкомасштабные и, казалось бы, не могут приводить к глобальным последствиям. Мы уже знаем, однако, что наличие интенсивных шумов в плазме может приводить к эффективному увеличению частоты столкновений частиц (рассеяние на волнах), вызывающему аномальные эффекты в процессах переноса: аномально высокая скорость диффузии и теплопроводность, аномально большое сопротивление плазмы и т.п.

Итак, кинетические неустойчивости есть следствие отступления от равновесной, максвелловской функции распределения. Неравновесные условия могут реализоваться не только при наличии пучка. Например, в адиабатической ловушке (§ 33) функция распределения «обедняется» за счет ухода медленных

204

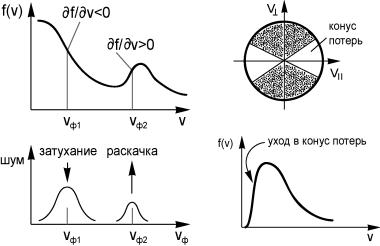
частиц в опасный конус потерь (рис. 4.23). Это создает благоприятные условия для раскачки разновидностей «конусных» неустойчивостей (например, одна из наиболее опасных –

дрейфово–конусная неустойчивость [12]), ограничивающих время жизни плазмы в ловушке.

Рис. 4.22. Резонансное взаимодейРис. 4.23. Неравновесная функция ствие волн и частиц в плазме распределения частиц в адиабати-

ческой ловушке

Причиной неустойчивости может быть и наличие потоков плазмы, если найдется подходящая волна с фазовой скоростью, близкой к скорости потока. Именно такова может быть ситуация при наличии систематических дрейфовых потоков плазмы (§ 17). Например, скорость ларморовского дрейфа, обязанного своим происхождением неоднородности плотности замагниченной плазмы, по порядку величины составляет

vдр ~ vT ρB 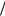L ,

где L – характерный размер неоднородности. С этой скоростью можно связать частоту соответствующей дрейфовой волны. Если, например, B||z, n||x, то волна распространяется в направлении оси y:

ω = ky vдр .

205

•Пучковая неустойчивость

Одним их простейших примеров кинетической неустойчивости является неустойчивость пучка электронов, пронизывающего плазму.

Рассмотрим наиболее простой случай раскачки продольных

волн, когда через холодную плазму (Te→0, Ti→0) noi=noe=no, проходит холодный пучок электронов (vno≠0, nno≠0) малой плотности. Дисперсионное уравнение для этого случая записывается в виде:

Первые два слагаемых здесь отвечают холодной плазме (см. § 29), а последнее описывает вклад холодного пучка электронов. Здесь ωLe, ωLi и ωп – ленгмюровские частоты для электронов плазмы, ионов плазмы и электронов пучка соответственно, vп – скорость электронов пучка.

Это полное уравнение 4-й степени, приводимое к канонической форме. Приближенное решение его было предложено Я.Фейнбергом из довольно наглядных физических соображений. Известно, что при прохождении пучка через плазму возникают (точнее, могут возникать при определенных условиях) колебания с нарастающей во времени амплитудой. Развивается так называемая пучковая неустойчивость. Она является частным случаем неустойчивостей, обусловленных наличием участков с положительной производной части функции распределения. Из рис. 4.22 видно, что с волной взаимодействуют частицы плазмы, скорость которых близка к скорости волны vф2. Кажется, возникает противоречие: сначала приняли Тe→0, а теперь должны принять, что часть электронов плазмы имеют тепловую скорость, близкую к фазовой скорости волны. Но условие Тe→0 еще не значит, что температура тождественно равна нулю (такого не бывает), а обозначает только, что скорости, приобретаемые в электрических полях, много больше тепловых. Следовательно, противоречия нет. Однако в нашем случае пренебрежем

Это уравнение всегда имеет решение с положительной мнимой частью, что и дает величину инкремента (скорости роста) возмущений:

206

Поскольку возмущения всех величин ( ne , vre , nn , vrn , E ) пропорциональны

e−iωt +ikrrr , то они будут увеличиваться пропорционально eγt . Величина γ называется инкрементом и определяет скорость нарастания амплитуды волны во времени. Заметим также, что возмущения для этой неустойчивости являются сносовыми (увлекаются пучком), так как решение имеет ненулевую действительную часть частоты. Важно отметить также, что изложенное приближенное решение позволяет оценить лишь величину максимального инкремента неустойчивости. Между тем, уже из самого уравнения (4.94)

очевидно, что короткие волны, для которых |k|>> ωLe 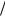vno , раскачиваться не

могут. Другими словами, неустойчивость имеет коротковолновый порог, как можно показать, равный

|kпорог|= 2(ωLe vno )[1 + (nn n0 )23 ]3 2 2(ωLe vno ). (4.98)

Порог, как мы видим, определяется величиной формально похожей на дебаевский радиус, однако вместо тепловой скорости, которая в нашем случае равна нулю, входит скорость частиц пучка.

Для других пучковых неустойчивостей инкременты будут другими. Например, для бунемановской (токовой) неустойчивости

относительного движения ионов и электронов, описываемой сходным с (4.94) уравнением

максимальный инкремент, как можно показать, будет зависеть от отношения масс электронов и ионов

Эта неустойчивость также пороговая, однако, в отличие от предыдущего случая, сноса нет и фактически это стоячие апериодически нарастающие возмущения.

При наличии пучков неустойчивости всегда имеют возможность развиваться, естественно, при условии преодоления порога, если в спектре шумов плазмы найдется возмущение с подходящей длиной волны.

207

Функция Лагранжа для материальной частицы равна разности между кинетической и потенциальной энергией L = T – U. Для электрона, движущегося в чисто электростатическом поле,

L = mv2/2 – (-eϕ). В присутствии магнитного поля B функция Лагранжа L = mv2/2 – (-eϕ) + (-e Avr/c), где A - векторный потенциал

магнитного поля ( B = rot A ). Вариационный принцип Гамильтона

δS = 0 называется принципом наименьшего действия (интеграл

t1

S = ∫Ldt называется интегралом действия, или просто действи-

ничный вектор, направленный по касательной к траектории, то движение частицы, при условии постоянства ее полной энергии (T + U = const), определяется аналогом принципа наименьшего дейст-

B r r

вия - принципом Мопертюи: δ ∫Pdl = 0 . Этот принцип для движе-

A

ния материального тела в постоянном потенциальном поле аналогичен принципу Ферма геометрической оптики для световых лу-

чей: δ ∫B ndl = 0 , который означает минимальность оптической дли-

A

ны на реальном пути света. То есть оптический путь для светового

луча ∫B ndl – самый короткий, где n – показатель преломления сре-

A

ды, dl –элемент траектории луча. Если n = const, то преломление луча отсутствует и свет распространяется прямолинейно. Из принципа Ферма вытекает известный закон преломления световых лучей, который задает соотношение между углом падения α и углом преломления β (углы между лучом и нормалью к границе раздела):

В случае электронов их компонента скорости, перпендикулярная электрическому полю, не меняется, а модуль скорости пропор-

209

ционален U , где U – потенциал относительно точки, в которой скорость электрона равна нулю. Поэтому в электронной оптике

U играет роль показателя преломления среды, а закон преломления имеет вид:

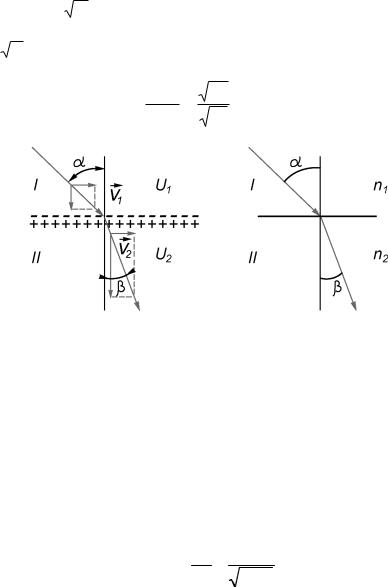
Рис. 5.2. Преломление пучка заряженных частиц на границе потенциалов (a) и света на границе двух сред (б)

если считать, что на границе раздела потенциал скачком меняется от U1 до U2. Резкий скачок потенциала на пути электронного пучка можно создать между двумя металлическими сетками с мелкими ячейками, расположенными на близком расстоянии друг от друга, (рис. 5.2). Таким образом, по аналогии со световой оптикой можно говорить об электронных лучах, и для них создавать аналогичные устройства фокусировки (линзы) и разделения по энергиям (спектрометры). Условие применимости геометрической оптики для электронов (т. е., когда электрон можно рассматривать как частицу) выполняется, когда длина волны электрона

λ[A&] = h ≈ 12.25 mv U[В]

(U – ускоряющее напряжение) мала по сравнению с характерным размером неоднородностей системы. Но у электронной оптики есть

210