Жданов Основы физических процессов 2007

и вновь пропорциональной полю волны. Здесь νei = τei−1 − частота

электрон-ионных столкновений, σˆ − проводимость плазмы. Для диэлектрической проницаемости получаем:

ω2

ε =1 − p . (4.28)

ω[ω + iνei (1 + Zme / Mi )]

Как мы видим, она становится величиной комплексной. Это является следствием того, что столкновения приводят к затуханию колебаний, то есть к диссипации энергии. Заметим, что в (4.28) теперь уже нельзя выделить отдельно вклад ионов и электронов - аддитивность вкладов нарушается из-за взаимодействия компонент плазмы. Подчеркнем еще одно важное обстоятельство. Использованные в (4.26) выражения для плотности сил взаимного трения между электронами и ионами

отличаются по знаку − так и должно быть для сохранения импульса в целом в ион-электронной системе, но, на первый взгляд, несимметричны при «буквенной» перестановке масс, зарядов и концентраций частиц. В действительности, необходимая симметрия имеет место. Достаточно вспомнить, что, как это было показано в § 9, эти параметры должны входить в выражение для времени между столкновениями ионов и электронов следующим образом:

Теперь, после подстановки в выражения для плотностей сил трения, требуемая симметрия становится очевидной.

В уравнениях (4.24), (4.26) мы пренебрегли эффектами, связанными с конечностью температуры плазмы, что справедливо

161

в высокочастотной области, когда выполнено условие (4.20). Чтобы продвинуться в область меньших частот, когда фазовая скорость волны оказывается одного порядка с тепловыми скоростями частиц, необходимо усложнить модель плазмы, включая эффекты конечного давления, что мы и собираемся теперь сделать. Вместе с тем для упрощения будем пренебрегать столкновениями ионов и электронов. Это возможно, если температура достаточно велика. Напомним, что частота ион-электронных столкновений быстро убывает с ростом температуры:

νei ~ Te−3/ 2 .

Если температура плазмы конечная, то в правые части уравнений движения (4.24) необходимо добавить слагаемые с градиентом давления. Пусть температура компонент плазмы постоянная, тогда градиент давления определяется градиентом

возмущения плотности:

~ = ~

pe,i Te,i ne,i ,

следовательно, уравнения движения необходимо дополнить уравнениями, определяющими возмущение плотности плазмы. Если число частиц плазмы сохраняется, то необходимые нам дополнительные соотношения дают уравнения непрерывности. Для малых возмущений на фоне однородной плазмы это уравнения вида:

Кроме модели плазмы с постоянной температурой, часто используется модель политропы, в которой давление и температура плазмы предполагаются степенными функциями плотности:

этого случая градиент давления для малых возмущений будет

равен

~ = γ ~

pe,i e,iTe,i ne,i .

162

Объединяя вместе все выше сказанное, приходим к следующей модели для «теплой плазмы»:

Здесь индекс α = e,i обозначает «сорт» частиц плазмы − ион или электрон. Так, например, ee = −e − заряд электрона, а ei = Z e − заряд иона. Вновь предполагая волны гармоническими, вычисляем

где, по аналогии с газом, для краткости введено обозначение csα

для «скорости звука» соответствующей компоненты плазмы. Умножив найденные скорости компонент плазмы на заряд и невозмущенную плотность, просуммировав затем результат по сортам частиц, вычисляем плотность электрического тока:

Воспользовавшись, далее, определениями (4.9), (4.10) получаем тензор проводимости:

а затем и тензор диэлектрической проницаемости:

163

В формулах (4.30), (4.31) индексы p, q нумеруют компоненты тензоров. Поскольку обсуждаемая нами сейчас модель плазмы в отсутствие волны является изотропной − нет никакого выделенного направления, то структура тензора диэлектрической проницаемости совпадает с предсказываемой формулой (4.14). Из сопоставления с этой формулой получаем продольную

диэлектрическую проницаемость. Они разные, поскольку учет теплового движения частиц плазмы приводит к появлению явной зависимости диэлектрической проницаемости от волнового числа. Сравнив (4.32), (4.33) с формулой (4.19) для холодной плазмы, мы видим, что изменение претерпевает только продольная диэлектрическая проницаемость, поперечная остается неизменной! Это связано с тем, что поперечная гармоническая волна малой амплитуды не изменяет плотности плазмы, следовательно, не появляется градиент давления, и конечность температуры несущественна.

В статическом пределе, то есть в пределе ω → 0 , продольная проницаемость оказывается равной

164

что совпадает с (4.22), если принять γe = γi = 1 , то есть считать

компоненты плазмы изотермическими.

Подчеркнем, что, строго говоря, учет теплового движения частиц плазмы требует кинетического описания. Поэтому приведенные результаты дают качественно правильную, но упрощенную картину диэлектрических свойств плазмы. Можно добиться лучшего согласия с точными результатами, если входящие в приведенные формулы показателиγe ,γi рассматривать

в качестве «подгоночных параметров», отбирая их в зависимости от конкретной решаемой задачи. Например, в случае, когда тепловые поправки можно считать малыми, но конечными, из формулы (4.32) приближенно получаем:

что совпадает с результатом кинетической теории [18] при выборе

γα = 3 .

§ 29. Поперечные электромагнитные волны в незамагниченной плазме

Вооружившись полученными в предыдущем параграфе результатами, рассмотрим процесс распространения электромагнитных волн в плазме. Как мы уже знаем (см. § 27) задача сводится к решению дисперсионных уравнений

εl = 0 ,

или

εtr = N 2

в зависимости от того, какой конкретно тип волны нас интересует: чисто продольные или чисто поперечные волны. Последний случай особенно прост. С него и начнем обсуждение плазменных волн.

Поскольку для поперечных волн диэлектрическую проницаемость плазмы определяет соотношение (4.33), то дисперсионное уравнение будет таким:

165

Решением этого уравнения, очевидно, является

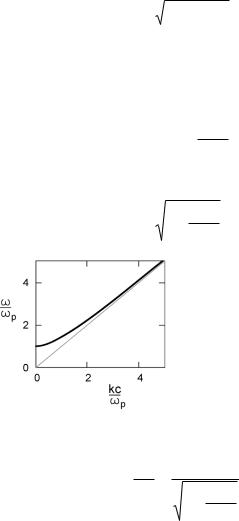
Это соотношение и определяет закон дисперсии поперечной волны в плазме (рис. 4.1). Обратим внимание, что для коротких волн, когда k→∞, получаем ω→kc, так что в этом пределе волна (4.36) становится обычной световой волной. Для длинных волн, когда k→0, приближенно

c2 k 2

ω≈ ωp 1 + 2ω2 .p

Заметим также, что для фазовой скорости волны закон дисперсии (4.36) дает значение

166

оказывается, как это и должно быть, меньше скорости света в вакууме.

§ 30. Явление отсечки низкочастотной поперечной волны

Как мы видим из формулы (4.36), частота поперечной волны в плазме всегда больше плазменной частоты, поэтому поперечные волны, частота которых меньше плазменной частоты, не могут в ней распространяться. Это означает, что падающая из вакуума на границу плазмы поперечная волна с малой частотой должна отражаться. Имеет место, как говорят явление отсечки волны (в английской литературе - cut off). Критическая частота − частота отсечки,

зависит от концентрации плазмы. Так что, измеряя критическую частоту, можно определить концентрацию плазмы. Это один из распространенных методов диагностики плазмы.

Электромагнитное поле низкочастотной волны частично все же проникает в плазму, но его амплитуда экспоненциально уменьшается вглубь плазмы. Глубина проникновения в плазму поля поперечной волны с низкой частотой определяется толщиной вакуумного скин-слоя, которая обратно пропорциональна плазменной частоте:

Таким образом, глубина проникновения волны в плазму определяется инерцией ее частиц, главным образом - электронов. В пренебрежении инерцией глубина проникновения поля была бы нулевой.

Проиллюстрируем сказанное простым примером. Пусть из вакуума на плоскую границу плазмы падает низкочастотная волна, слева направо, как это показано на рис. 4.2. Слева и справа от границы раздела законы дисперсии волны разные:

167

где функция f задает поле волны: например, это может быть компонента напряженности электрического поля. На границе раздела потребуем выполнения условий непрерывности:

Нетрудно найти решение задачи (4.39), (4.40), удовлетворяющее этим условиям. Предлагаем читателю проверить, что таковым является решение, в котором в области вакуума поле складывается из поля падающей и отраженной волны, а в области плазмы волновое поле экспоненциально затухает:

где обозначено

168

- коэффициент пространственного затухания поля волны в плазме, f0 − амплитуда падающей на границу раздела волны. Амплитудные коэффициенты α для отраженной волны и β для поля в плазме, как это вытекает из условий непрерывной сшивки (4.40), оказываются равными:

Обратим внимание, что числитель и знаменатель первой формулы являются комплексно-сопряженными. Поэтому получаем

|α|= 1 ,

и, следовательно, амплитуды падающей волны и отраженной совпадают. Это и означает наличие полного отражения падающей на плазму волны.

В пределе совсем низких частот, когда ω → 0 , получаем приближенно

и длина затухания поля в плазме совпадает с длиной вакуумного скин-слоя.

§ 31. Ленгмюровские колебания и волны в плазме. Плазмоны

Рассмотрим теперь закон дисперсии высокочастотных продольных плазменных волн с частотой в области ленгмюровской частоты. Они известны как ленгмюровские волны и представляют собой важнейший тип возмущений, способных существовать и распространяться в плазме.

Закон дисперсии продольных волн определяет, как было показано выше, уравнение

εl = 0 ,

в которое следует подставить продольную компоненту диэлектрической проницаемости. Если плазму считать холодной, то диэлектрическую проницаемость следует определять по формуле (4.19), и мы приходим к уравнению

169

ω2

1 − ωp2 = 0 .

Оно имеет два решения, отличающиеся знаком. Положительный корень равен

Как мы видим, в рассматриваемом случае частота волны совпадает с ленгмюровской частотой и не зависит от величины волнового числа. Фазовая скорость таких волн

уменьшается с увеличением волнового числа, а групповая скорость оказывается равной нулю:

Таким образом, в холодной плазме ленгмюровские волны не могут переносить энергию: фактически это обычные колебания плотности заряда, возникающие вследствие нарушения квазинейтральности плазмы. Если же мы учтем теперь тепловое движение частиц плазмы, то ситуация изменится кардинально. Диэлектрическую проницаемость определяет теперь формула (4.32) и дисперсионное уравнение для продольных волн становится таким:

Это уравнение несложно решить в общем виде. Но в интересующей нас сейчас высокочастотной области следует учесть, что ионы плазмы можно считать неподвижными, а потому их вклад в диэлектрическую проницаемость будет пренебрежимо малым.

170