ГЛАВА 7
ЭМИССИОННАЯ ЭЛЕКТРОНИКА
Большинство плазменных установок представляют собой газоразрядные устройства. Возникновение разрядов в системах с электродами сопряжено не только с обменом зарядами между твердым телом и плазмой, но и без эмиссии электронов с поверхности вообще невозможно. Кроме того, эмиссионные явления широко используются в различных приборах для диагностики плазмы. В данной главе кратко будут рассмотрены основные существенные в исследованиях и применениях плазмы виды эмиссии электронов из поверхности твердых тел.
§44. Термоэлектронная эмиссия
Электроны в металлах
«Электронный газ» в металлах представляет собой электроны зоны проводимости, возникшие как обобщенные валентные электроны атомов при сближении атомов на расстояния, когда перекрываются электронные облака отдельных атомов. Сплошная зона проводимости возникает из-за расщепления энергетических уровней электронов отдельных атомов в силу запрета нахождения электронов в одинаковом квантовом состоянии. Так как число атомов велико, то расщепленные уровни электронов образуют непрерывную энергетическую полосу, называемую зоной проводимости, в которой электроны можно считать свободными, т.е. не привязанными к какому-либо атому. С другой стороны, оставшиеся без электрона атомы, т.е ионы играют роль нейтрализующего электроны фона, так что электронный газ и ионы кристаллической решетки можно считать плазмой. Однако расстояние между иона-
|
1 |
1 |
|
−9 |
|
ми: |
|
≈ |
|
=10 |
|
м становится меньше длины волны де |
n1/ 3 |
(1027 )1/ 3 |
|
Бройля электрона:
241
|
λ = |
h |
≈ 6.6 10−34[ Дж с] ≈10−9 |
м, (h – постоянная Планка). |
|
|
e |
meve |
|
|
kT |
|
|
|
|
|
|
|
|
me |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
Следовательно, |
электрон |
|
f (E) |
|
|
|
нельзя считать частицей, т.е. |
|
|
|
|
|
|
|
|
|
плазма становится квантово вы- |
|
|
T=0 |
|
|
рожденной, |
подчиняющейся |
|
|
|
|
|
уже не классической статистике |
|
|
|
|
|
Максвелла-Больцмана, |
а стати- |
|
EF |
|
|
стике Ферми-Дирака. При этом |
|
|
|
|
2kT |
|
|
|
электрон |
необходимо |
описы- |
|
|
|
|
вать |
волновой |
функцией, |
Рис.7.1. Распределение Ферми- |
|
имеющей смысл плотности ве- |
|
роятности |
нахождения |
Дирака |
|
|
|
|
электрона в данной точке в данный момент времени: |
|
|
|
|
ψ (rr,t)=ψ k (rr) ϕ(t)= 1 exp(ikrrr)exp(− iωt), |
|
(7.1.) |
|
|
|
2π |
|
|
V |
|
|
|
|
|
где |
k = |
- волновой вектор, |
|
pz |
|
|
|
|
L |
|
|
|
|
|
|
|
|
V = L3 – объем металла, ω – часто- |
pF |
|
py |
|
та волны. Энергия электрона в со- |
0 |
|
|
|
стоянии ψ k : |
|
|
|
|
px |
|
|
|
|
|
|
|
|
Ek = |
p2 |
h2 k 2 |
|
|
|
|
|
|
k |
= |
|
. |
|
|
|
|
|
|
Рис.7.2. Сфера Ферми в |
|
2me |
2me |
|
|
|
|
|
импульсном пространстве. |
Функция |
распределения |
Ферми- |
|
|
|
|
Дирака, т.е. число частиц в одном состоянии: |
|
|
|
f (E)= |
|
1 |
|
|
|
(7.2) |
|
|
|
|
E − E |
F |
|
|
|
|
|
|
|
|
|
|
|
|
1+ exp |
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 7.1). Импульс электрона можно выразить через квантовое
|
r |
r |
h r |
число |
s : |
p = |
|
s , так что компоненты импульса |
L |
px = Lh sx , py = Lh sy , pz = Lh sz где sx , sy , sz целые положительные и отрицательные числа. Элементарный кубик в импульсном про-
странстве имеет объем h3 , поэтому число возможных квантовых
L3
состояний в объеме dpx dpy dpz равно L3 dpx dpy dpz . При T = 0 все h3
электроны находятся внутри так называемой сферы Ферми (рис. 7.2). Если учесть принцип Паули и две возможные ориентации
|
|
3 |
|
|
4 |
3 |
|
|
L |
|
|
|
|
3 |
|
|
πpF |
= N , |
спина, то число состояний в сфере Ферми: 2 |
|
|
3 |
h |
|
|
|
|
|
|
|
|
3n |
0 |
1/ 3 |
N |
|
|
следовательно pF |
= h |
|
|
, где n0 = |
|
. Тогда энергия Ферми |
|
8π |
V |
|
|
|
|
|
|
равна:
= p2 = h2
EF F
2me 2me
Энергия Ферми не зависит от объема металла, а зависит от концентрации свободных электронов. На первый взгляд странный вывод. При росте V число N растет, казалось бы, должно расти число уров-
ней и верхний уровеньEF должен повышаться, но EF не зависит от общего
числа уровней. Это связано с тем, что уменьша-
|
3n |
2 / 3 |
h2 |
|
(3π 2n0 ) |
2 / 3 |
|
|
|
0 |
|
= |
|
|
|
. |
(7.3) |
8π |
|
|
|
|
|
|
2me |
|
|
|
ρ(E) |
|
|
|
T = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EF |
|
|
E |
|
|
2kT |
|
|
|
|
|
|
Рис. 7.3. Функция распределения электронов по энергии
ется расстояние между уровнями E = NE/F2 (с учетом спина), и
зона проводимости при N → ∞ становится сплошной. Число час-
тиц с |
энергией |
меньше |
|
E |
|
|
определим |
из соотношения |
E = |
h2 |
(3π 2n)3/ 2 |
, следовательно: |
|
|
|
|
2m |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n (E )= |
1 |
|
2m E 3/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
, |
(7.4) |
|
|
|
|
|
|
3π |
2 |
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда плотность частиц (число частиц, имеющих энергию от E до E |
+ dE) dn = |
1 |
( |
2m |
)3 / 2 E1/ 2 dE . С учетом распределения Ферми- |
2π 2 |
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
Дирака функция распределения электронов в металле имеет вид:
ρ (E ) = |
dn |
= |
1 |
2m 3/ 2 |
E1/ 2dE |
|
|
. |
(7.5) |
|
|
|
h2 |
|
|
|
|
dE |
π 2 |
E − E |
F |
|
|
|
2 |
|
|
|
1+ exp |
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
Плотность термоэмиссионного тока
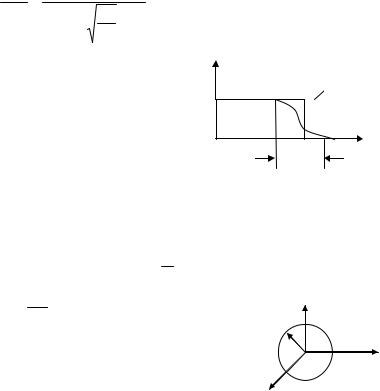
Испускание электронов нагретыми проводящими материалами называется термоэлектронной эмиссией. Это явление было обнаружено в 1883 г. Эдисоном. Аналитический расчет плотности термоэмиссионного тока можно получить исходя из модели Зоммерфельда о нахождении электронов в металле как в потенциальной яме. При абсолютном нуле температуры энергия электронов металла не может быть больше энергии Ферми, поэтому ни один электрон не может выйти из металла, а функция распределения обрывается при E=EF (рис. 7.3). При Т > 0 обрыв сглаживается, появляется «хвост» функции распределения электронов с энергиями больше EF, именно у этих электронов, количество которых экспоненциально растет с ростом температуры поверхности, появляется ненулевая вероятность преодоления потенциального барьера на границе металла. Поэтому термоэмиссионный ток заметен только для нагретых тел. Его величина рассчитывается интегрированием функции распределения по нормальной составляющей к поверхности энергии Wx в пределах интегрирования от Wa до ∞ , где Wa -

высота потенциального барьера. С учетом вероятности преодоления потенциального барьера, а также с учетом того, что для термоэлектронов Wx - EF >> kBT , плотность термоэмиссионного тока мо-
жет быть представлена формулой Ричардсона-Дэшмана:
j |
= AT 2 exp(− |
eϕa |
) , |
(7.6) |
|
T |
|
kBT |
|
|
|
|
где ϕa = Wa - EF – работа выхода электрона из материала катода, равная наименьшей энергии, которую нужно сообщить электронам для их эмиссии, kB – постоянная Больцмана. Величину A = A0D , учитывающую прозрачность барьера между металлом и вакуумом D = (1 - r ), r – коэффициент отражения электронов от барьера, усредненный по энергиям электронов, иногда называют «постоянной Ричардсона», где
A |
0 |
[ |
А |
] = |
4πmek B |
2 |
= 120 .4 |
(7.7) |
см2 |
К 2 |
h 3 |
|
|
|
|
|
|
|
универсальная термоэлектронная константа, называемая постоянной Зоммерфельда. Следует учесть, что работа выхода зависит от температуры (вследствие теплового расширения), обычно эта зависимость линейная:
ϕa = ϕ0(T0) + α(T-T0), |
(7.8) |
α = dϕ/dT|T=To = 10-5 ÷ 10-4 эВ/град – температурный коэффициент, который может быть для разных металлов как положительным, так и отрицательным. Значение постоянной Ричардсона А для разных металлов изменяются от 15 до 350 А/(см2 К2). Экспериментальное определение работы выхода ϕa и «постоянной» Ричардсона А можно провести по методу «прямой Ричардсона», полагая вблизи некоторой температуры T0 линейное изменение ϕа(Т) (7.8) и строя по экспериментальным данным зависимость ln(jT/T2) от 1/T. По тангенсу угла наклона полученной прямой определяют работу выхода ϕa, а точка пересечения прямой с осью ординат дает значение ln(A)
.
− e Er x
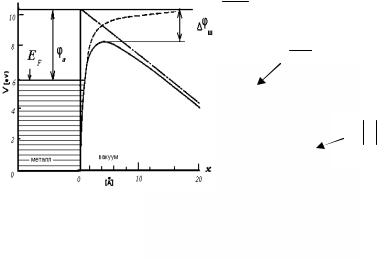
Рис. 7.4. Потенциальный барьер на границе металл – вакуум
(7.9)
(7.10)
Зависимость (7.6) для плотности термоэмиссионного тока можно получить, если рассматривать термоэмиссионный ток как поток электронов в вакуум, имеющих распределение Больцмана в потенциальном поле и преодолевающих потенциальный барьер eϕa (термодинамический вывод):
jТ = enevср/4,
где
ne |
= 2 |
m k T 3/ 2 |
|
e B |
|
|
2πh |
2 |
|
|
|
|
|
− плотность невырожденного электронного газа,
термодинамическая скорость.
При отсутствии (или пренебрежимо малой) напряженности ускоряющего электроны внешнего электрического поля эмитированные электроны создают около поверхности отрицательный пространственный заряд, ограничивающий ток термоэмиссии. Поэтому, в слу-
чае малых напряжений между катодом и анодом термоэмиссионный ток можно приравнять плотности тока j3/2, тогда зависимость плотности тока jТ от напряжения на аноде jТ Ua3/2. При дальнейшем увеличении Ua объемный заряд у катода исчезает и, казалось бы, ток должен выйти на насыщение, при котором все эмитированные электроны уходят на анод. Однако, как показали эксперименты, при дальнейшем увеличении Ua так, при напряженностях поля ~ 104 В/см, ток эмиссии продолжает медленно расти ( exp(E1/2)). Рост электронного тока эмиссии под действием внешнего электри-

ческого поля вследствие уменьшения работы выхода электрона из твердого тела из-за понижения в поле потенциального барьера
(рис. 7.4)
называется эффектом Шоттки. Потенциальную энергию электрона на расстоянии x от поверхности металла с учетом сил зеркального отображения заряда и внешнего электрического поля E можно описать в виде (см. рис.7.4):
|
eU (x) = EF |
+ eϕa |
− |
e2 |
−eEx |
(7.12) |
|
4x |
|
|
|
|
|
|
Снижение работы выхода можно оценить из соотношения (7.12) на вершине потенциального холма, положение которого соответствует координате:
а потенциальная энергия в максимуме
eUm = EF + eϕa - e3/2E1/2. |
(7.14) |
Снижение работы выхода за счет эффекта Шоттки:
e ϕш[эВ] = e3/2E1/2 = 3.79 10-4 E1/2 [В/см]. |
(7.15) |
Плотность термоэмиссионного тока с учетом эффекта Шоттки:
jТШ = jT exp(e3/2E1/2/kBT) = jT exp(4.39E1/2[В/см]/T[K]). |
(7.16) |
Влияние поверхностной неоднородности материала катода на термоэмиссию
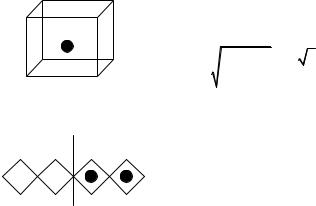
Тугоплавкие металлы, использующиеся для термокатодов, такие, как вольфрам, тантал, молибден, имеют объемноцентрированную кубическую (ОЦК) решетку (рис.7.5).
BC
Аa D
Рис. 7.5. Схема ОЦК
Плотность атомов в разных гранях различная, она определяется расстоянием между атомами. Например, расстояние между точками
|
AF = |
a2 |
+ |
a2 |
= |
a 3 |
меньше, чем |
|
2 |
4 |
2 |
|
|
|
|
|
между AD = a .
|
|
|
Следовательно, |
плотность атомов |
|
|
|
в плоскости грани АА1С1С больше, |
|
|
|
чем в плоскости AA1D1D. Поверх- |
|
|
|
ность металла можно представить в |
|
|
|
виде зубцов различных граней кри- |
|
участок 1 |
участок 2 |
сталла, обращенных в вакуум. Если |
|
соседствуют участки с разной плот- |
|
ϕa1 |
< ϕa 2 |
ностью атомов, то такие участки об- |
|
ладают разной работой выхода элек- |
|
|
|
|
Рис. 7.6. Участки неодно- |
тронов, т.к. уровень заполнения |
|
электронного облака |
проводимости |
|
родной поверхности |
зависит от концентрации ионов ней- |
|
|
|
|
|
|
трализующего фона. Например, на |
|
|
|
участке 2 (рис.7.6) |
с |
гранями, со- |
|
|
|
держащими больше |
атомов, элект- |
роны будут ближе находиться к поверхности (чисто геометрически) по сравнению с участком 1 и тем самым будут в большей степени компенсировать положительные заряды зубцов, создающих вытягивающее поле. Другими словами, можно сказать, что электроны легче удерживаются в плоскости граней, содержащих большую концентрацию атомов, т.е на участке 2 работа выхода электронов будет больше, чем на участке 1. Тогда поверхность даже чистого поликристаллического металла можно рассматривать как пятнистую с областями, обладающими различной работой выхода. Работа выхода пятен соответствует работе выхода однородного массивного образца лишь при достаточных размерах этих пятен l >10-20 нм, при меньших размерах электронная структура меняется.
Рис. 7.7. Поверхность с неоднородной работой выхода
l |
EП |
|
ϕmin ϕmax |
ϕ min ϕmax |
Возникающая между этими областями контактная разность потенциалов, создает над незаряженной металлической поверхностью электрическое поле. Это поле можно
назвать полем пятен EП . Оно
направлено таким образом, что тормозит электроны, эмитированные пятнами с малой ра-
ботой выхода и ускоряет электроны на участках с большой работой выхода. Т.о. коллективное действие плазмы металла стремится нивелировать возникающие неоднородности эмиссионной способности поверхности. При этом изменяется потенциальная энергия
|
электронов: eU = EF + eϕa − |
e2 |
−eEx ± eEП xП . Таким образом, |
|
4x |
|
|
|
для эмиссии электронов с участков с ϕmin возникает дополнитель-
∞
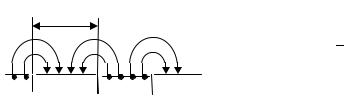
ный потенциальный барьер величиной U = ∫EП dx (рис.7.8). На-
0
до учесть, что xП < x (область действия поля пятен меньше облас-
ти действия внешнего электрического поля). На больших расстояниях внешнее электрическое поле «возьмет свое» и «загнет» ход кривой потенциальной энергии. Поэтому максимум все равно будет, так что дополнительный потенциальный барьер будет равен
xкр
U1 = ∫(EП − E)dx , где значение xкр определяется из соотноше-
0
ния EП (xкр )= E . При увеличении внешнего поля E дополнительный потенциальный барьер U1 уменьшается, и термоэмисси-
онный ток резко возрастает. Этот эффект получил название аномального эффекта Шоттки. Это аномальное увеличение тока
прекратится, как только барьер исчезнет т.е. EП = E .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eϕ |
|
eϕmax |
|
|
|
При |
дальнейшем |
уве- |
|
|
|
|
U |
личении E эмиссия с |
|
|
|
|
|
U1 |
|
областей, |
имеющих |
|
eϕmin |
E << EП |
− eEx |
ϕmin , |
будет |
происхо- |
|
дить |
независимо |
от |
|
|
|
|
|
|
|
|
|
− eEx |
пятен с ϕmax , увеличе- |
|
|
W |
F |
|
E >> EП |
|
|
|
ние тока термоэмиссии |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
будет соответствовать |
|
|
|
|
|
xкр |
|
|
|
снижению работы вы- |
|
|
|
|
|
|
|
|
|
хода |
по нормальному |
|
|
Рис. 7.8. Изменение потенциального |
|
эффекту Шоттки. |
|
|
|
барьера полем пятен. |
|
|
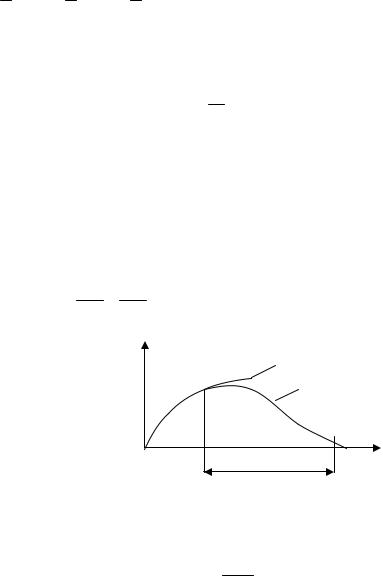
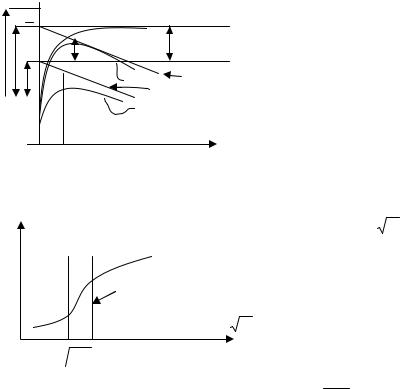
По экспериментальной |
|
|
|
|
|
|
|
зависимости |
ln j( |
E ) |
|
|
|
ln j |
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 7.9) можно опре- |
|
|
|
|
|
|
|
|
|
делить порядок |
элек- |
|
|
|
|
|
|
участок аномального |
трических полей пятен |
|
|
|
|
|
|
эффекта Шоттки |
EП , |
а скачок |
(ln j) |
|
|
|
|
|
|
|
E |
имеет порядок |
разно- |
|
|
|
|
|
|
|
|
|
сти |
работ |
выхода |
 EП
EП
Рис. 7.9. Зависимость плотности термоэмиссионного тока от напряженности внешнего электрического поля
δϕ = ϕmax −ϕmin :
(ln j)= ekTδϕ .
δϕ
Учитывая, что EП ~ δy , можно оценить характерный размер
пятен. Поле пятен возникает не только над поликристаллической поверхностью металла, но и в случае покрытия поверхности катода тонкой неоднородной пленкой адсорбированных атомов.
Так как ток термоэмиссии сильно зависит от работы выхода поверхности (7.6), то адсорбция электроположительных элементов (щелочных или щелочноземельных) сильно понижают ϕа увеличивая jТЭ, в то время как адсорбция электроотрицательных (O,Cl,S,C) приводит к обратному. Если поверхность имеет участки с разной работой выхода (что может происходить при соприкосновении




 E
E