Жданов Основы физических процессов 2007

где x - среднее смещение частицы при хаотических блужданиях, а τ -время между столкновениями. Для диффузии частиц в газе или плазме x соответствует средней длине свободного пробега λ . Учитывая, что τ = λ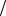vT , получаем

D ~ λvT ,

где vT = 3T m -средняя тепловая скорость частиц.

Элементарная кинетическая теория газов приводит к следующим выражениям для коэффициентов диффузии, вязкости и

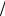где ρ = mn -массовая плотность, cV - удельная теплоемкость газа при постоянном объеме, Для одноатомных газов cV = (32)(km)

(если определять теплоемкость в системе СГС) Напомним, что температуру мы измеряем в энергетических единицах. Это означает, что во всех выражениях можно формально полагать постоянную Больцмана k равной единице.

Следует подчеркнуть, что выражения (1.63)- (1.65) получены для простого газа, образованного из одинаковых частиц массой m . В этом случае коэффициент D является по существу коэффициентом самодиффузии D11 , т.е. диффузией выделенных («ме-

ченых») частиц в среде собственных молекул. Под концентрацией n следует понимать в этом случае плотность именно этих меченых молекул (например радиоактивного изотопа в смеси практически одинаковых по массе молекул).

Поясним, как возникают соотношения (1.63)-(1.65) на примере вычисления диффузионного переноса частиц (самодиффузии) в газе. Пусть газ является слабонеоднородным вдоль одной координаты (например, вдоль координа-

61

ты x ). Рассмотрим плоскость, перпендикулярную оси х, и выделим на ней еди-

ничную площадку. Будем предполагать, что молекулы, летящие по направлению к этой площадке, претерпевают последние столкновения на расстоянии

средней длины свободного пробега частиц λ и далее движутся к ней без

столкновений. Учтем также, что при изотропном распределении молекул по направлению скоростей в заданном направлении движется в среднем 1/6

часть молекул. Тогда их поток определяется выражением N = (16)nvT . Результирующая плотность потока частиц, пересекающих выделенную площадку в направлении оси x , определяется как разность потоков молекул, летящих с левой и правой стороны относительно площадки,

σ = π a2 , где a - диаметр шара. Для рассматриваемого слабо неоднородного состояния газа плотность n в выражении для средней длины свободного

пробега, а следовательно и длинуλ , можно приближенно полагать постоянными. Воспользуемся также малостью этой величины. Например, при нормальных условиях ( T = 273K и p =1 атм) плотность газа равна числу Лош-

мидта n ≈ 2.7 1019 см-3, , а λ имеет порядок 10-6 см., если a = 5Ao . Это позволяет использовать приближенные разложения плотности в ряды вида

Это выражение по своей структуре аналогично определению диффузионного потока (1.59), направленного вдоль оси x Коэффициент пропорциональности

в нем и есть коэффициент самодиффузииD11 (1.63).

Аналогичным образом можно получить выражение и для потока тепла qx . Учитывая, что средняя энергия теплового движения частиц равна cV mT ,

где T -температура газа, которая теперь меняется вдоль оси x (плотность n предполагается постоянной), находим

Сравнение с (1.60) показывает, что смысл коэффициента теплопроводности имеет величина

62

которая совпадает с определением (1.65).

Для получения тем же способом выражения для коэффициента вязкости рассматривается перенос импульса поперек потока газа (вдоль оси x ), кото-

рый движется со скоростью uz (вдоль оси z ). Площадка, через которую рас-

сматривается перенос импульса, располагается в некотором положении x , перпендикулярно оси x . Рассматривая разность значений импульсов, перено-

Коэффициент пропорциональности в этом выражении соответствует коэффициенту вязкости η , определяемому формулой (1.64)

Получаемые в элементарной кинетической теории выражения для коэффициентов переноса дают правильные зависимости от основных параметров газа, отличаясь от точных значений лишь численными коэффициентами. При этом в соответствии с результатами строгой кинетической теории газа коэффициенты переноса для модели молекул – твердых упругих шаров – связаны соотношениями [50 ]:

Из этих выражений следует, в частности, что коэффициенты вязкости и теплопроводности газа нейтральных частиц для рассмотренной выше модели молекул меняются с температурой пропор-

симости может несколько меняться, если используются более реалистические модели взаимодействия молекул (например, потенциал Леннарда-Джонса). Подробную информацию по этому вопросу можно найти, например, в монографии [50].

63

Вязкость плазмы

Для плазмы, образованной из электронов, ионов и нейтральных молекул, с существенно различающимися массами электронов и тяжелых частиц, анализ явлений переноса оказывается более сложным, чем в случае простого нейтрального газа. Однако ряд важных качественных выводов о характере зависимости электронных и ионных коэффициентов переноса от массы частиц и температур компонентов плазмы может быть сделан и на основе элементарных представлений.

Выражение для коэффициента вязкости (1.64), даваемое элементарной теорией, можно представить также в виде:

где τ - характерное время свободного пробега между столкновениями (время релаксации).

Для слабоионизованной плазмы ее вязкость определяется главным образом взаимодействием нейтральных молекул, а вклад электронной и ионной вязкости оказывается малосущественным.

Принимая для оценок, что сечение взаимодействий молекулы σ = πa2 = const , получаем

Существенно, что вязкость не зависит от давления газа.

С ростом степени ионизации решающим становится роль кулоновских взаимодействий частиц. Нетрудно показать, что основной вклад в вязкость полностью ионизованной плазмы дает ионая компонента. Из-за малости массы электрона по сравнению с массой иона вклады электронной и ионной вязкости могут быть раз-

64

Электронная вязкость определяется как электрон-электронными, так и электрон-ионными столкновениями. Поскольку, однако

τee = 2τei , то с учетом выражения для τee (1.44) имеем

Очевидно, что при Te = Ti

ηe ηi = (me Mi )12 <<1,

поэтому вкладом электронной вязкости в полную вязкость плазмы можно пренебречь. Однако ее вклад может оказаться сравнимым с

вязкостью ионов для неизотермической плазмы при Te >> Ti , если

выполнено условие Te Ti ~ (Mi me )15 .

Существенно, что в соответствии с (1.74) ионная вязкость гораздо сильнее зависит от температуры, чем вязкость нейтральной компоненты. Отметим, что коэффициенты вязкости ионов и электронов для полностью ионизованной плазмы, получаемые метода-

ми строгой кинетической теории, даются выражениями [51]:

Теплопроводность плазмы

Теплопроводность слабоионизованной плазмы определяется переносом тепла только нейтральными частицами. В соответствии с (1.65)

С ростом степени ионизации и возрастанием роли кулоновских столкновений существенный вклад начинает вносить теплопроводность, обусловленная электронами. Соответствующие оцен-

При Te = Ti имеем

65

κi κe = (me Mi )12 <<1.

Это означает, что основной вклад в теплопроводность полностью ионизованной плазмы вносит электронная теплопроводность. Вклад теплопроводности ионов может оказаться сравнимым с электронной теплопроводностью для неизотермической плазмы с

Ti > Te при выполнении условия Ti Te ~ (Mi me )15 .

Коэффициенты теплопроводности, получаемые в строгой кинетической теории, имеют вид [51,52]

Различие в числовых коэффициентах, даваемых элементарной и строгой теорией, оказывается в этом случае большим, чем при вычислении вязкости плазмы, однако основные качественные зависимости полностью сохраняются.

Диффузия в плазме

Прежде чем перейти к рассмотрению диффузии и оценкам коэффициентов диффузии в плазме, дадим более четкое определение понятия плотности диффузионного потока частиц. сорта k , где индекс k может соответствовать электронам, ионам и нейтральным частицам (k = e,i.a). Диффузионные потоки данного компо-

нента связаны с направленным движением его частиц в какойлибо заданной системе отсчета. Обычно выбирают систему отсчета, связанную с так называемой среднемассовой скоростью плазмы

ция) и средняя направленная скорость частиц k -го компонента плазмы. Выбор такой системы отсчета удобен, поскольку именно среднемассовая скорость входит в уравнения магнитной гидродинамики плазмы (см. главу 3). Для слабоионизованной плазмы

66

( ne , ni <<1) скорость u фактически совпадает со скоростью ней-

трального компонента ua . Для полностью ионизованной плазмы из-за условия me << Mi эта скорость практически равна скорости

ионов ui .

Плотность диффузионного потока частиц k -го компонента (будем называть ее просто диффузионным потоком ) определяется как

Пусть концентрации компонентов nk меняются вдоль оси x . Если

к плазме приложено еще электрическое поле E , то диффузионный поток k -го компонента вдоль направления x может быть представлен в виде:

Здесь Dk и μk - соответственно коэффициенты диффузии и подвижности k -го компонента в плазме, Zk -кратность заряда (зарядовое число), для электронов Ze = −1 . Из общих термо-

динамических соображений можно показать , что коэффициенты диффузии и подвижности связаны соотношением Эйнштейна:

Элементарная кинетическая теория, основанная на понятии средней длины свободного пробега (см. начало этого раздела), дает возможность получить выражение для коэффициента диффузии только для случая так называемой самодиффузии, когда массы частиц газа примерно одинаковы. Поэтому вопрос о диффузии частиц в плазме мы рассмотрим на основе другого приближенного подхода, который можно назвать “методом баланса импульса”.

Суть этого метода состоит в следующем. Предполагается, что для установившихся во времени процессов переноса частиц в плазме может быть записано некоторое уравнение баланса, в кото-

67

быть пропорциональна плотности частиц k-го компонента и средней частоте столкновений νkj с частицами других сортов. Приве-

денная массаμkj появляется в выражении, поскольку столкновения частиц при вычислении Rk рассматриваются в системе отсчета,

связанной с их центром масс.

Обратимся к случаю слабоионизованной плазмы. Уравнения баланса импульса для электронов и ионов (с кратностью заряда Z )

вплазме можно представить в виде

−dpdxe − neeE = −ne meνea (ue − ua ),

выписывать уравнение баланса для нейтральных частиц, поскольку в силу квазинейтральности плазмы суммирование его с уравнениями (1.86) дает слева и справа тождественный нуль, т.е это уравнение не является независимым.

Тогда с использованием (1.86) получаем

69

Коэффициенты подвижности μe и μi выражаются через De и Di с помощью соотношения (1.83).

Средние частоты упругих столкновений электронов и ионов с атомами можно определить как

где g -модуль относительной скорости частиц, а 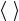означает усре-

днение по максвелловскому распределению частиц по скоростям.

Для модели твердых упругих шаров νea, ≈ naσeaveT , νia, ≈ naσiaviT и мы приходим к оценкам

т.е. коэффициент диффузии электронов (и соответственно подвижность) в слабоионизованной плазме оказывается во много раз больше коэффициента диффузии (подвижности) ионов.

В случае полностью ионизованной плазмы достаточно записать одно уравнение баланса вида

В отличие от случая слабоионизованной плазмы коэффициент диффузии Dei , который определяется кулоновскими взаимодействиями частиц, очень сильно зависит от температуры .

70