
Непейвода. Прикладная логика
.PDF
5.4. ФУНКЦИИ |
|
101 |
где R X × Y — функциональное соответствие. X называется обла- |
||
стью определения f, Y — |
ее областью значений. |
Область определения |
обозначается Dom f, а область значений — Val f. |
|
|
Прошу обратить внимание на различие области значений и образа |
||
функции. f hXi Y , но равенства обычно нет. |
|
|
В последнее время композиция функций в математике определяется |
||
в соответствии с композицией отношений: |
|
|
(f ◦ g)(x) = g(f(x)),
а чтобы при композиции функции не переставлялись, и применение функ- |
||
ций во многих местах (в частности, в работах по алгебре) стали писать |
||
“ наоборот30”: xf. |
|
|
Определение 5.4.2. (Важные классы функций) |
|
|
1. Инъекция (однозначное отображение) — |
такая функция f, что |
|
x X y X(f(x) = f(y) x = y). |
|
|
2. Сюръекция (отображение на) — |
|
|
y Y x X f(x) = y. |
|
|
3. Биекция (взаимно-однозначное отображение) — функция, у кото- |
||
рой существует обратная, т. е. функция, графиком которой служит |
||
отношение, обратное к графику f. |
= Val f. Для инъекций |
|
Таким образом, для сюръекций f hDom fi |
||
множество f−1 hyi всегда не более чем одноэлементно (здесь f−1 — |
от- |
|
ношение, обратное к f, оно не обязательно является функцией, и поэто- |
||
му использовано обозначение образа, принятое для соответствий). Еще |
||
две важных характеризации инъекций и сюръекций на языке компози- |
||
ций заслуживают отдельного рассмотрения и доказательства. |
|
|
30 Неразбериха с порядком функций при композиции длилась несколько десятилетий Прямая школа считала в точности наоборот и до сих пор во. многих“ работах” по математическому анализу :и(дифференциальнымf ◦ g)(x) = f(g(x))уравнениям, при держиваются такого определения В принципе здесь что в лоб что по лбу но не запу- тывайтесь! . , , , -

102 ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Предложение 5.4.1. (Композиции с инъекциями и сюръекциями) |
||||
1. |
Композиция двух инъекций — |
инъекция. |
||
2. |
Композиция двух сюръекций |
— |
сюръекция. |
|
3. |
f : X → Y инъекция тогда и только тогда, когда для любых двух |
|||
|
отображений g1, g2 из Z в X |
|
||
|
|
g1 ◦ f = g2 ◦ f g1 = g2. |
||
4. |
f : X → Y |
сюръекция тогда и только тогда, когда для любых |
||
|
двух отображений g1, g2 из Y |
в Z |
||
|
|
f ◦ g1 = f ◦ g2 g1 = g2. |
||
5. |
f : X → Y инъекция тогда и только тогда, когда существует |
|||
|
функция g : |
Y → X (называемая накрытием, ассоциированным |
||
|
с f), такая, |
что |
|
|
|
|
x(x X g(f(x)) = x). |
||
|
(Другими словами, f ◦ g = idX |
.) |
||
6. |
f : X → Y |
сюръекция тогда и только тогда, когда существует |
||
|
функция g : |
Y → X (называемая ретракцией, ассоциированной с |
||
|
f), такая, что |
|
|
|
|
|
x(x Y f(g(x)) = x). |
||
|
(Другими словами, g ◦ f = idY .) |
|||
Доказательство. |
Пункты 1, 2 и 4 остаются в качестве упражнений чи- |
|||
тателю. |
|
|
|
|
Доказательство пункта 3. Пусть f — инъекция из X в Y . Пусть |
||||
g1 ◦ f |
= g2 ◦ f. Тогда для произвольного x f(g1(x)) = f(g2(x)). Но |
|||
по инъективности f отсюда следует g1(x) = g2(x). Поскольку вывод |
||||
сделан для произвольного x, g1 = g2 |
, что и требовалось установить. Те- |
|||
перь обратно. Пусть для всех g1, g2 |
, таких, что g1 ◦f = g2 ◦f, выполнено |
|||
равенство g1 = g2. Возьмем произвольные x1, x2. Пусть f(x1) = f(x2). |
||||
Теперь возьмем одноэлементное множество Z = {z0} и построим два
5.4. ФУНКЦИИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
|||||||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
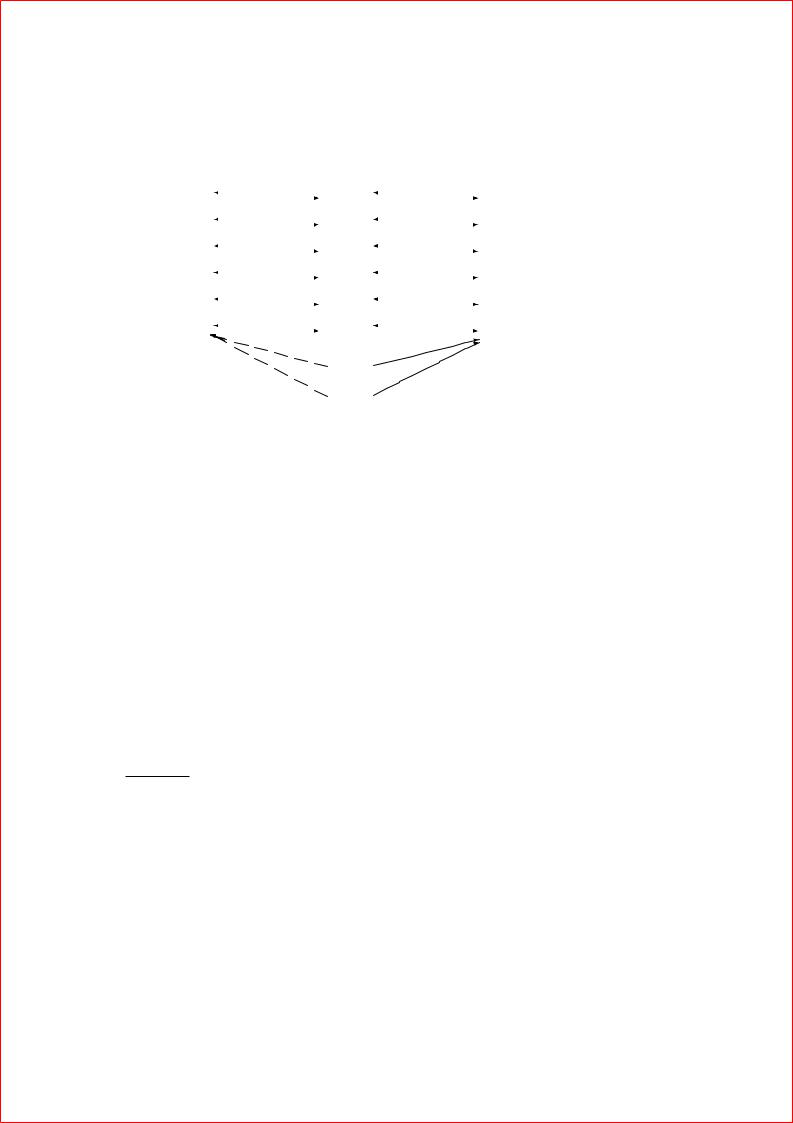
Рис. 5.6: Инъекция и накрытие, сюръекция и ретракция
отображения из Z в X, такие, что g1 |
(z0) = x1, g2(z0) = x2. Поскольку |
||||||
f(g1(z0)) = f(g2 |
(z0)), а других значений аргумента нет, g1 ◦ f = g2 ◦ f. |
||||||
Значит, в частности, |
g1(z0) = g2(z0), и x1 = x2. Прошу Вас обратить |
||||||
внимание, что в этом доказательстве |
нет рассуждений от противного. |
||||||
Поэтому данное свойство инъекций весьма устойчиво при смене логи- |
|||||||
ки. Доказательство пункта 5. Пусть у f есть ассоциированное с ним на- |
|||||||
крытие g. Покажем, |
что тогда f — |
инъекция. В самом деле, возьмем |
|||||
произвольные x1, x2 |
, такие, что f(x1) = f(x2). Тогда g(f(x1)) = x1 = |
||||||
g(f(x2)) = x2. Теперь в обратную сторону. Пусть f — |
инъекция. По- |
||||||
строим накрытие g следующим образом: если y f hDom fi, то имеет- |
|||||||
ся единственное x, такое, что f(x) = y. Оно и будет значением функции |
|||||||
g. Если же y / f |
h |
Dom f |
i |
, то такого x вообще нет, и можно задать зна- |
|||
|
|
|
|
31 |
. |
||
чение g равным произвольно выбранному элементу x0 |
|||||||
31 Здесь есть тонкость Прямое и обратное рассуждения принципиально различают ся по логическому статусу! Если прямое рассуждение весьма устойчиво то обратное- содержит внешне безобидный. шаг требующий анализа бесконечно большого, объема информации проверка принадлежит, ли Поэтому вторая часть данной эквивалентности: легко,рушится при заменеy fлогикиhDom fиiдаже. просто при отходе от тео рии множеств в качестве основания математики. -

104 |
|
|
ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ |
||||||
Доказательство пункта 6. Поскольку f — сюръекция, для каждого |
|||||||||
y Val f |
множество R−1 hyi непусто. Сопоставим каждому y какой- |
||||||||
элементов R−1 |
h |
y |
i |
. Полученная функция и будет искомой ре- |
|||||
либо из 32 |
. |
|
|
|
|
|
|
||
тракцией |
|
|
|
|
|
|
|
|
|
Обратная импликация очевидна, поскольку, чтобы вернуться к ар- |
|||||||||
гументу, нужно его порою выдавать в качестве значения, что и является |
|||||||||
определением сюръекции. |
|
|
|
|
|||||
Предложение 5.4.2. Функция является биекцией тогда и только тогда, |
|||||||||
когда она является и инъекцией, и сюръекцией. |
|
|
|||||||
Доказательство. |
Пусть отношение R — график функции f. Рассмо- |
||||||||
трим отношение |
R−1. Поскольку f — |
сюръекция, для каждого x Y |
|||||||
существует y X, (x, y) R−1. Поскольку f — |
инъекция, |
из (x, y1) |
|||||||
R−1, (x, y2) R−1 следует y1 = y2. |
Таким образом, R−1 — |
функцио- |
|||||||
нальное отношение. |
|
|
|
|
|
|
|
||
Обратная функция, если она существует, обозначается f−1.
Предложение 5.4.3. f ◦ f−1 = IdDom f , f−1 ◦ f = IdVal f .
Доказательство оставляется в качестве упражнения.
|
ситуация еще хуже. Подумайте, а как мы выберем по элементу из каждого |
|||
32 А здесь |
||||
R−1 hyi? То, что такой выбор можно осуществить, на самом деле эквивалентно одной |
||||
из аксиом современной теории множеств, причем аксиоме, чаще всего берущейся под |
||||
сомнение: аксиоме выбора. Она гласит, что по любому всюду определенному соответ- |
||||
ствию можно построить вложенное в него функциональное. |
Из нее следуют многие |
|||
приятные теоремы традиционной математики и некоторые неприятные, например, те- |
||||
орема Куратовского о том, что яблоко можно разрезать на четыре части таким образом, |
||||
что из них можно сложить два таких же яблока. В науке всегда так: сильный принцип, |
||||
полезный в одних отношениях, вреден и сбивает с толку в других областях. Ни один по- |
||||
лезный научный результат не универсален, потому что наука — |
отрасль человеческого |
|||
знания, а человек несовершенен, и поэтому его знания также с необходимостью несо- |
||||
вершенны. Так что если кто-то уверяет Вас, что его метод всегда хорош, то это либо |
||||
жулик, либо человек, слишком увлекшийся своей идеей, настолько, что она уже нахо- |
||||
дится у него на стадии перехода из ценной в сверхценную (‘ценная’ здесь — |
обычная |
|||
неформальная оценка, ‘сверхценная’ — |
термин из психиатрии, применяемый, когда че- |
|||
ловек зацикливается на одной идее и не видит больше ничего вокруг Надо сказать что нынешняя система организации науки внедрившая в нее рекламу которая). всегда была, противопоказана науке поощряет такое, жульничество будьте осторожнее, и осмотри тельнее! , , -

5.4. ФУНКЦИИ |
105 |
Определение 5.4.3. Множества X и Y называются равномощными, если |
|
имеется биекция X на Y . Мощность множества X не больше мощности |
|
множества Y (X 6 Y ), если имеется инъекция из X в Y . Множество Y |
|
покрывает множество X (X < Y ), если имеется сюръекция X на Y . |
|
Теорема |
5.2. (Кантор, Шредер, Бернштейн) Если X 6 Y и Y 6 X, |
то X и Y |
равномощны. |
Доказательство. Пусть X 6 Y и Y 6 X. Тогда имеются две инъекции: |
|
f : X → Y , g : Y → X. Если хоть одна из них является сюръекцией, то |
|
эквивалентность установлена. Если ни одна из них не является сюръек- |
|
цией, то множество X \ g hY i непусто. Возьмем произвольный элемент |
|
x0 этого множества. Возьмем отношение |
|
|
4 |
|
|
|
|
R = {(x1, x2) | x1 X & x2 X & x2 = g(f(x1))} . |
|||||
Рассмотрим его транзитивное замыкание R∞. Образ x0 при этом замы- |
|||||
кании либо конечен, либо бесконечен. Рассмотрим эти два случая. |
|||||
Пусть образ |
R∞ hx0i конечен. Тогда он состоит из конечного мно- |
||||
жества элементов |
|
|
|
||
|
x0, x1 |
4 |
4 |
4 |
|
|
= g(f(x0)), x2 |
= g(f(x1)), . . . , xn = xn−1. |
инъекция, |
||
g(f(xn)) = xi для некоторого i < n. Но поскольку f ◦ g — |
|||||
i = 0. В самом деле, если i 6= 0, |
то i = j +1, но тогда xj+1 = g(f(xj)) = |
||||
g(f(xn)), |
где xj |
6= xn, чего не может быть. Но по предположению x0 |
|||
X \ g hY i, и соответственно, нет такого y, что x0 = g(y). |
|
||||
Значит, остается лишь случай, когда образ x0 бесконечен. Все эле- |
|||||
менты этого образа, очевидно, лежат в g hY i. Докажем теперь, что обра- |
|||||
зы разных x X \ g hY i при соответствии R∞ не пересекаются. Рассу- |
|||||
ждение аналогично тому, с помощью которого мы опровергали конеч- |
|||||
ность R∞ hx0i. Возьмем произвольные x, y X \ g hY i. Если их обра- |
|||||
зы пересекаются, то некоторые из xn равны некоторым из ym. Возьмем |
|||||
наименьшее такое n. Если оно не |
0, то xn−1 6= ym−1, но g(f(xn−1)) = |
||||
Теперь построим, пользуясь выше установленным разбиением X, |
|||||
g(f(ym−1)). |
|
|
|
|
|
биекцию Y на X. Для этого видоизменим функцию g. Положим |
|||||
g1(y) = |
g(y) ¬ x(g(y) R∞ hxi & x X \ g hY i) |
|
|||
xn−1 |
x n(x X \ g hY i & g(y) R∞ hxi & g(y) = xn) |
||||
Итак, все последовательности xn |
сдвигаются на один элемент, и в ре- |
||||
зультате g1, оставаясь инъекцией, |
становится и сюръекцией. |
|
|||

106 ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Понятие равномощности дает возможность расклассифицировать мно- |
||
жества по отобразимости друг на друга33. |
|
|
Прежде всего конечные множества равномощны тогда и только то- |
||
гда, когда у них одинаковое количество элементов. Это можно было бы |
||
“ доказать,” но уже с конца XIX века известно, что на самом деле лишь |
||
понятие равномощности дает возможность корректно определить ко- |
||
нечное множество в теории множеств. |
|
|
Определение 5.4.4. Множество X называется конечным, если оно рав- |
||
номощно множеству |
|
|
{x | x N & x < n} |
|
|
для некоторого n N. |
|
|
Количество элементов в конечном множестве будем обозначать N X. |
||
В упражнениях разбираются другие попытки определить конечные |
||
множества. |
|
|
Соответственно, бесконечному множеству чаще всего дают в ма- |
||
тематике негативное определение: бесконечное множество — |
множе- |
|
ство, не являющееся конечным. Нетривиальное определение бесконеч- |
||
ного множества дал Рассел: |
такое множество X, что |
|
Определение 5.4.5. Бесконечное множество — |
||
существует взаимно-однозначное отображение X на какое-либо под- |
||
множество Y X & Y 6= X. |
|
|
Таким образом, бесконечное множество равномощно своему под- |
||
множеству34. Безусловно, математик обязан обосновать, что любое мно- |
||
жество либо конечно, либо бесконечно. Самый простой и одновременно |
||
33 Обычно в книгах по математике пишут, что по числу элементов. Это верно лишь |
|
для конечных множеств. Для бесконечных, скорее, это классификация по сложности |
|
представления. Далее мы познакомимся подробнее с тем, почему общепринятые пред- |
|
ставления не верны и в данном случае. |
|
34 Видимо, первым обратил на это внимание кардинал Николай Кузанский , выдающий- |
|
ся схоласт XV века. Он применил это для обоснования того, что триединство Бога не |
|
является логическим противоречием, поскольку Бог — |
бесконечная сущность (одно из |
очень немногих корректных применений математики в богословии Галилей видимо независимо заметил что множество натуральных чисел взаимно однозначно). , отобра, жается в частности, ,на множество четных чисел и опубликовал это- в математическом- тексте ,Отсюда Галилей, сделал вывод что нельзя, говорить о множестве всех натураль ных чисел. поскольку иначе нарушается, фундаментальная аксиома Евклида Целое- больше части, В дальнейшем математики просто отказались от этой аксиомы: « заме тив, что ее нельзя». выразить на математическом языке. , -

5.4. ФУНКЦИИ |
|
|
107 |
выявляющий некоторые скрытые трудности, путь к этому — |
через кон- |
||
кретный вид бесконечных множеств: счетные множества. |
равномощное |
||
Определение 5.4.6. Счетное множество — |
множество, |
||
множеству натуральных чисел N. |
|
|
|
Предложение Если множество содержит счетное подмноже ство, то оно бесконечно5.4.4. . -
Доказательство Пусть имеется биекция множества натуральных чи сел на Тогда. построим следующееfвзаимно однозначное отобра- жениеY Xна. Если то положим Если - 6 ϕ Xто существуетX \ f(0). такоеx / YN, что ϕ(x) =Тогдаx. положимx Y ,
x = f(0), n , x = f(n + 1).
ϕ(x) = f(n).
Предложение Всякое бесконечное множество содержит счет ное подмножество5.4.5.. -
Доказательство Пусть имеется биекция множества на
Тогда возьмем. какое либо f X обозначимY X, егоY 6= XДалее. подобно тому как- делалосьx0 Xв\теоремеY . f(x0Кантора) 6= x0, Шредера Бернштейнаx1. ,положим , и так же как в упомянутой- теоре- ме можно показать, чтоxnвсе+1 = fразличны(xn), Множество, -
, , xi .
{xi | i N}
и есть искомое счетное подмножество X.
Предложение Если множество не является конечным то оно содержит счетное5.4.6.подмножество. ,
Доказательство Рассмотрим следующее отношение между конечны ми подмножествами. X: -
4
E = {(Y, Z) | Y X & Z X & Y Z & N Y + 1 = N Z} .
Итак данное отношение связывает между собою конечные множества второе, из которых содержит один дополнительный элемент вдобавок к, элементам первого Очевидно что не определено на тогда и только тогда когда . Но поскольку, поE условию не являетсяY конечным E всегда, определеноY = X. . X ,

108 |
|
|
ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ |
|
||||||
|
Поэтому начнем с |
некоторого одноэлементного множества V0 |
|
X, |
||||||
|
|
35 |
|
|
|
|
|
|||
и для каждого Vi выберем |
|
Vi+1 как произвольный элемент E hVii. Оче- |
||||||||
видно, |
что Vi Vj при i < j, и объединение возрастающей последова- |
|||||||||
тельности |
|
|
4 ∞ |
|
|
|
|
|
||
|
|
|
|
|
[ |
|
|
|
|
|
|
|
|
|
|
V = |
Vi |
|
|
|
|
и есть искомое счетное подмножество X. |
|
|
|
|
||||||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
Итак, мы показали, что действительно, каждое множество либо ко- |
|||||||||
нечно, |
либо бесконечно и что счетные множества являются в некотором |
|||||||||
смысле минимальными среди бесконечных. Но счетных множеств не |
||||||||||
так уж мало. |
|
|
|
|
|
|
|
|
||
Пример 5.4.1. Множество рациональных чисел счетно. В самом деле, |
||||||||||
любое рациональное число представимо несократимой дробью |
n/m, |
|||||||||
где m > 0. Дробей с суммой числителя и знаменателя k — |
конечное |
|||||||||
число, |
поэтому их можно расположить в порядке возрастания n, |
за ни- |
||||||||
ми все дроби с суммой числителя и знаменателя n + 1 и так далее. |
|
|
||||||||
|
На самом деле мы дали общий способ, как показать счетность лю- |
|||||||||
бого множества, элементы которого представимы конечной последова- |
||||||||||
тельностью из конечного числа символов. |
|
|
|
|
||||||
|
Мощность множества натуральных чисел часто обозначается 0 ( — |
|||||||||
первая буква еврейского алфавита, произносящаяся ‘алеф’). Простей- |
||||||||||
ший пример бесконечного множества, |
не являющегося счетным, следу- |
|||||||||
ющий: |
|
|
|
|
|
|
|
|
|
|
Теорема 5.3. Множество действительных чисел несчетно. |
|
|
|
|
||||||
Доказательство. Пусть имеется некоторое отображение (последователь- |
||||||||||
ность) an множества |
N в действительные числа из отрезка [0, 1]. По- |
|||||||||
строим по ней представленное в троичной системе число b, не входя- |
||||||||||
щее в данную последовательность, и, более того, такое, что от данного |
||||||||||
an |
оно отличается уже первыми n + 1 |
членами троичного разложения. |
||||||||
a0 |
не принадлежит по крайней мере одному из трех отрезков [0, 1/3], |
|||||||||
35 Здесь опять применяется аксиома выбора но на самом деле здесь используется бо лее слабая ее форма вызывающая меньше сомнений; и самое главное совместимая с- аксиомой детерминированности, также естественной, но противоречащей, аксиоме вы бора Тех кто интересуется данным, вопросом можно,отослать например к книге -
См.также. , § 10.5.1. , , , [17].

5.4. ФУНКЦИИ |
109 |
[1/3, 2/3], [2/3, 1]. Выберем первую после запятой троичную цифру так, |
|||
чтобы b не попало в тот же отрезок, что и a0. Далее, пусть, например, |
|||
первая цифра это |
1. Тогда a1 не принадлежит по крайней мере одному |
||
из трех отрезков (а возможно, и ни одному из них, если оно не попада- |
|||
ет в [1/3, 2/3]) [1/3, 4/9], [4/9, 5/9], [5/9, 2/3]. Выберем вторую троич- |
|||
ную цифру таким образом, чтобы a1 разошлось с b. Так же продолжаем |
|||
и далее. Итак, никакая последовательность не может перечислить всех |
|||
действительных чисел. |
|
|
|
Обратим Ваше внимание на одну тонкость в приведенном доказа- |
|||
тельстве. Может показаться, что мы брали троичное, а не двоичное раз- |
|||
ложение с той целью, чтобы избавиться от хлопот с числом |
1/2. Ко- |
||
нечно, часто математики поступают именно так, делая гораздо труднее |
|||
реализуемый алгоритм лишь потому, |
чтобы не рассматривать отдель- |
||
но несколько исключительных случаев. Но здесь причина другая. Мы |
|||
постарались, чтобы данное доказательство было абсолютным, сохра- |
|||
няющим силу не только в традиционной математике, но и в ее извест- |
|||
ных модификациях. Мы, в частности, |
нигде не предполагали, |
что дей- |
|
ствительные числа точно известны, и проследили, чтобы для каждого |
|||
использованного в рассуждении отношения между ними можно было |
|||
указать, с какой точностью его достаточно проверить. |
|
||
Про множества, равномощные множеству действительных чисел, го- |
|||
ворят, что они имеют мощность континуума, эта мощность обозначает- |
|||
ся c. |
|
|
|
Пример 5.4.2. Любое конечномерное пространство Rn имеет мощность |
|||
континуума. |
|
|
|
В самом деле, воспользуемся определением действительных чисел |
|||
через двоичные разложения и построим инъекцию из Rn в R |
следую- |
||
щим образом ((x)i в данной формуле — |
i-тый знак числа x): |
|
|
|
(ϕ((x1, . . . , xn)))n i+k = (xk+1)n |
(5.15) |
|
Итак, двоичные знаки получившегося числа соединяют двоичные знаки |
|||
всех аргументов, |
и, очевидно, каждое из xi однозначно восстанавлива- |
||
ется по значению |
ϕ((x1, . . . , xn)). Инъекция R в Rn очевидна. |
|
|
По теореме Кантора-Шредера-Бернштейна, R и Rn равномощны.
Вопрос существуют ли множества мощности промежуточной меж ду счетной,и континуумом не разрешим в принятой, аксиоматике тео- рии множеств Предположение, что таких множеств нет носит название-
континуум-гипотезы. . , ,

110 ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Теорема 5.4. (Теорема Кантора) Множество всех подмножеств мно- |
|||||||||||||
жества X, обозначаемое P X, имеет мощность большую´ |
, чем X. |
||||||||||||
Доказательство. Очевидно, что имеется инъекция X в P X. Докажем, |
|||||||||||||
что обратной инъекции нет. |
|
|
что f — |
такая инъекция, к абсурду. Для |
|||||||||
Приведем предположение, |
|||||||||||||
этого построим множество |
|
|
|
|
|
|
|
|
|
|
|
||
4 |
{ |
x |
| |
x |
|
X & x / f− |
1 |
h |
x |
i |
. |
|
|
K = |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
Тогда f(K) K ¬ f(K) K.
Из теоремы Кантора следует парадокс Кантора показывающий что множества всех множеств не существует. , ,
(Парадокс Кантора) Множество всех множеств U содер- |
|
жит любое другое множество как подмножество, и значит, |
|
если V — |
некоторое множество, то имеется инъекция V в |
Но тогда имеется и инъекция в что противоречит теоремеU. Кантора. P U U,
Таким образом не всякое выразимое на языке логики свойство мно жеств определяет ,множество на самом деле проще всего здесь при- мер из парадокса Рассела несуществование( В современ- ной математике принято совокупности: множеств{x | иx других/ x}). математиче- ских объектов удовлетворяющих данному свойству называть класса- ми36 Классы не, могут быть элементами других классов, и тем более- множеств. Таким образом классы рассматриваются скорее, как сокра щения а не. как объекты Доказано, что добавление классов к обычной- теории, множеств ничего.существенно, не меняет
Есть интересный критерий позволяющий свести. вопрос является ли данная совокупность множеством, к этому же вопросу для, уже из вестных множеств Область значений ,любой функции определенной на- множестве сама является. множеством Если избавиться, от функции то критерий примет, следующий вид: . ,
36 В традиционной логике понятие класса означало совокупность объектов удовлетво ряющих данному свойству Г Кантор создатель теории множеств ввел новое, понятие- потому, что стал рассматривать. . и сами, множества как элементы множеств, .
