Непейвода. Прикладная логика

5.3. ОТНОШЕНИЯ

91

5

4

3

Y

2

1

0

X

Рис. 5.4: x − y —

целое число

Прообраз элемента y при соответствии R —

множество всех таких

x, что (x, y) R. Образ x при соответствии R обычно обозначается

через R hxi

X (Y1

Y ) — объединение

Образ (прообраз) множества X1

образов (прообразов) его элементов.

Образ X при соответствии R так-

же обычно обозначается через

R

h

X

i

.

Как

говорят, конкретный смысл

20

операции здесь устанавливается по контексту

.

R определено на x, если образ x

непуст.

R не определено на x, если образ x пуст.

Конечно же, поскольку от-

Рассмотрим операции над отношениями.

ношения являются множествами, над ними можно производить обыч-

ные булевы операции,

поскольку они —

подмножества прямого произ-

ведения, можно находить их проекции.

Но есть и специфические для

бинарных отношений операции.

Первая из них —

нахождение обратного отношения. Она сопоста-

вляет отношению R между A и B отношение R−1 (часто обозначаемое

также R) между B и A, определяемое следующим образом:

^

R−1 = {(y, x)|x A & y B & (x, y) R}.

(5.7)

Например, для изображенного на рис. 5.4

отношения обратным является

оно само, для отношения < —

отношение > и т. п.

Интересны два подкласса отношений между X и X (обычно назы-

ваемых отношениями

на X).

Определение 5.3.3.

Симметричным называется такое R, что R−1 = R.

Антисимметричным —

такое R, что R−1 ∩ R = .

Понятия симметричности и антисимметричности выражаются на язы-

ке логики:

x y((x, y) R (y, x) R),

x y((x, y) R (y, x) / R).

Важным частными отношением на X является диагональ, или единич-

ное соответствие,

или тождественное отображение21:

idX

= {(x, x)|x X} = {(x, y)|x = y}.

Эта диагональ является графиком функции λx.x, перерабатывающей ка-

ждое x само в себя.

Рефлексивным называется отношение, содержащее

Определение 5.3.4.

5.3. ОТНОШЕНИЯ

93

Итак, при композиции мы связываем x и z посредством такого y, что

y соответствует x согласно R и y

соответствует z согласно S. Очевидно,

что если отношения имеют вид

R = {(x, y)|x X & y Y & y = f(x)},

(5.8)

S = {(x, y)|x Y & y Z & y = g(x)},

то их композиция представляется как

R ◦ S = {(x, y) | x X & y Z & y = g(f(x))}.

(5.9)

Приведем некоторые важные алгебраические свойства композиции

отношений.

(ассоциативность)

R ◦ (S ◦ T ) = (R ◦ S) ◦ T

(5.10)

R ◦ idY = R

idX ◦ R = R

id —

единица

(5.11)

(R ◦ S)−1 = (S−1 ◦ R−1)

обратный к композиции

(5.12)

Но вот R ◦ R−1

= idX

выполнено отнюдь не всегда.

И последние из “ джентльменского набора”

классов отношений —

транзитивные и антитранзитивные отношения.

Чисто формально легко

написать определяющие их логические условия,

но и в данном случае

лучше связать эти понятия с операцией композиции над отношениями

на X.

Квадрат

×

Определение

5.3.6.

22

n

X

X —

отношение R2 =

отношения R

R ◦ R. Соответственно определяется

R :

Rn = R ◦ · · · ◦ R .

| n{zраз

}

94

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

Отношение называется2транзитивным, если R2 R. Отношение

антитранзитивно,

если R ∩ R = . Понятия транзитивности и анти-

транзитивности имеют выражение на логическом языке. Мы приведем

его для транзитивности, а для антитранзитивности выразите сами.

x y z((x, y) R & (y, z) R (x, z) R).

(5.13)

С транзитивностью связано важное понятие —

транзитивное замыка-

ние отношения23

. Дадим два определения транзитивного замыкания и

докажем их эквивалентность.

наименьшее множество, обладающее свой-

Определение 5.3.7.

1. X —

ством A, если A(X) и

Y (A(Y ) Y X).

2. Транзитивное замыкание отношения R X × X —

наименьшее

отношение

R∞ X × X, такое, что R∞ содержит все элементы

из R и R∞

транзитивно.

3. Транзитивное замыкание отношения R X × X —

∞

R∞ =

Rn

n=1

[

4. Транзитивное замыкание отношения R X × X —

пересечение

всех транзитивных отношений, включающих R:

R \X,

X

(5.14)

X транзитивно

примененная при определении транзитивного замыкания,

на самом деле

23 Схема,

—

общая схема, используемая при превращении структур, не обладающих замкнутостью

относительно некоторой операции, в структуры, замкнутые относительно нее. Так, на-

пример, двоично-рациональные числа (числа вида

2nm ) получаются замыканием целых

чисел относительно операции деления на 2; комплексные числа —

замыканием дей-

5.3. ОТНОШЕНИЯ

95

Докажем, что три определения R∞ эквивалентны. В самом деле,

n=1

содержит

и транзитивно

поскольку если

∞

Rn

R

,

(x, y)

Rn, (y, z)

R ,

то

(x, z)

R

. Любое транзитивное отношение, содержащее R,

S

n+m

n

m

должно содержать и все R (это легко доказывается по индукции). Зна-

чит

n=1

наименьшее транзитивное отношение

содержащее

,

∞

Rn —

,

R,

что иSтребовалось доказать. И, наконец, пересечение семейства транзи-

тивных отношений само транзитивно, а семейство из (5.14)

включает, в

частности, и минимальное из транзитивных расширений

R24.

Если отношение транзитивно и антирефлексивно,

оно называется

отношением (частичного)

порядка

и обозначается символом < либо

похожими на него

(например, ). Если отношение транзитивно и ре-

флексивно, то оно называется отношением предпорядка и обозначается

символом, похожим на 6 (например, <). Частичный порядок называет-

ся линейным, если выполнено условие

x y(x y x = y y x).

Множество с заданным на нем отношением частичного порядка на-

зывается

частично упорядоченным множеством (чум)25

Множество с

отношением предпорядка

—

пум. Множество с отношением линейного

порядка —

линейно упорядоченное множество (лум).

Предпорядок называется строгим предпорядком (или нестрогим по-

рядком), если выполнено

96

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

·1

·1

a2·

·b a·

·b

·c

a1·

·0

·0

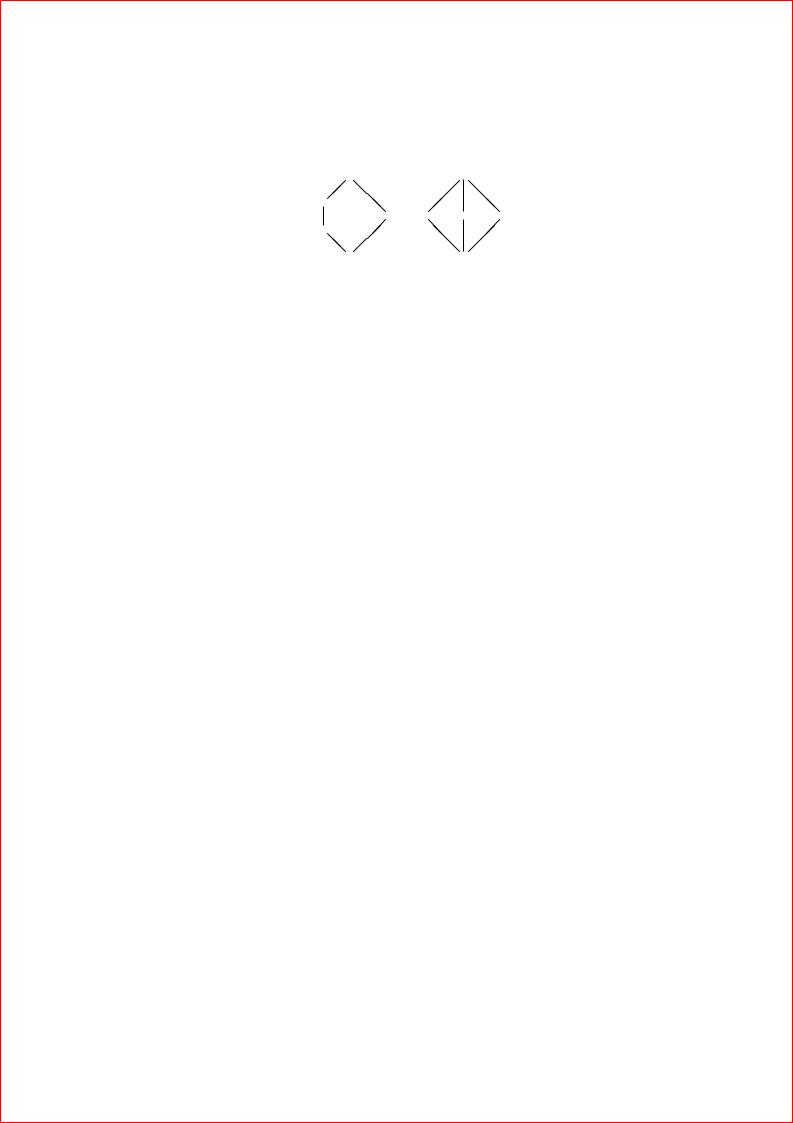
Рис. 5.5: Диаграммы Гессе двух важных пятиэлементных множеств

26 Хотя фактически частенько чиновники занимают позицию “ Начальник моего началь-

ника —

не мой начальник,” и соответственно, приказания Президента не исполняются

чаще,

чем повеления непосредственного шефа, но формально такое поведение проти-

воречит законам и инструкциям.

младшие по званию считаются больше

27 То, что здесь старшинство “ перепутано” —

старших, —

частный случай того математического факта, что R —

отношение порядка

ттт R−1 —

отношение порядка. Этот порядок называется обратным к R.

5.3. ОТНОШЕНИЯ

97

Соответственно определяются минимальный и наименьший элементы.

Элемент a называется

верхней гранью множества Y X (обозначается

sup Y либо S Y ), если

Соответственно определяется нижняя грань (inf Y ,

Y ). Верхняя (ниж-

няя) грань двух элементов обозначается a b (a ∩T

Чум в котором у

каждых двух элементов имеется верхняя и нижняя грань,

существуют

b).

,

наибольший и наименьший элементы, называется структура. Структу-

ра называется полной, если верхние и нижние грани существуют у лю-

бого подмножества элементов.

чум. Тогда на множестве X∞ кортежей

Определение 5.3.9. Пусть X —

98

ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ

5.3.3. Проверьте следующие тождества:

1.

(A B) × C = (A × C) (B × C)

2.

(A ∩ B) × C = (A × C) ∩ (B × C)

Если некоторые из них не всегда выполнены, в какую из сторон

имеет место вложение?

5.3.4. Верно ли, что

R ◦ R−1?

5.3.6. Каковы обратные отношения к следующим отношениям:

1.

Быть отцом.

2.

Быть мужем.

3.

Быть начальником.

4.

y = a · x.

5.

Быть братом.

6.

Быть братом или сестрой.

7.

Любить.

8.

Ненавидеть.

9.

Воевать.

1.

(R1 R2) ◦ S = (R1 ◦ S) (R2 ◦ S)

2.

(R1 ∩ R2) ◦ S = (R1 ◦ S) ∩ (R2 ◦ S)

5.3.5. Когда (x, x) R◦R−1? Выведите из Вашего условия, когда idX

5.3.7.

Построить композиции следующих отношений (‘Быть A’ означа-

ет ‘x является A для y’. Математические формулы рассматрива-

ются на множестве действительных чисел):

a)

Быть родителем

Быть отцом

б)

Быть родителем

Быть сестрой

в)

Быть соседом

Быть другом

г)

Быть другом

Быть соседом

д)

Быть мужем

Быть отцом

е)

x > y

y > x

ж)

x2 = y

y2 = x

з)

x = ey

x = sin y

5.4. ФУНКЦИИ

99

5.3.8. Отношение порядка, для которого выполнено R◦R = R, называ-

ют плотным. Почему? Переведите данное условие на логический

язык.

5.3.9. Докажите, что для любого отношения предпорядка R ◦ R = R.

5.3.10.

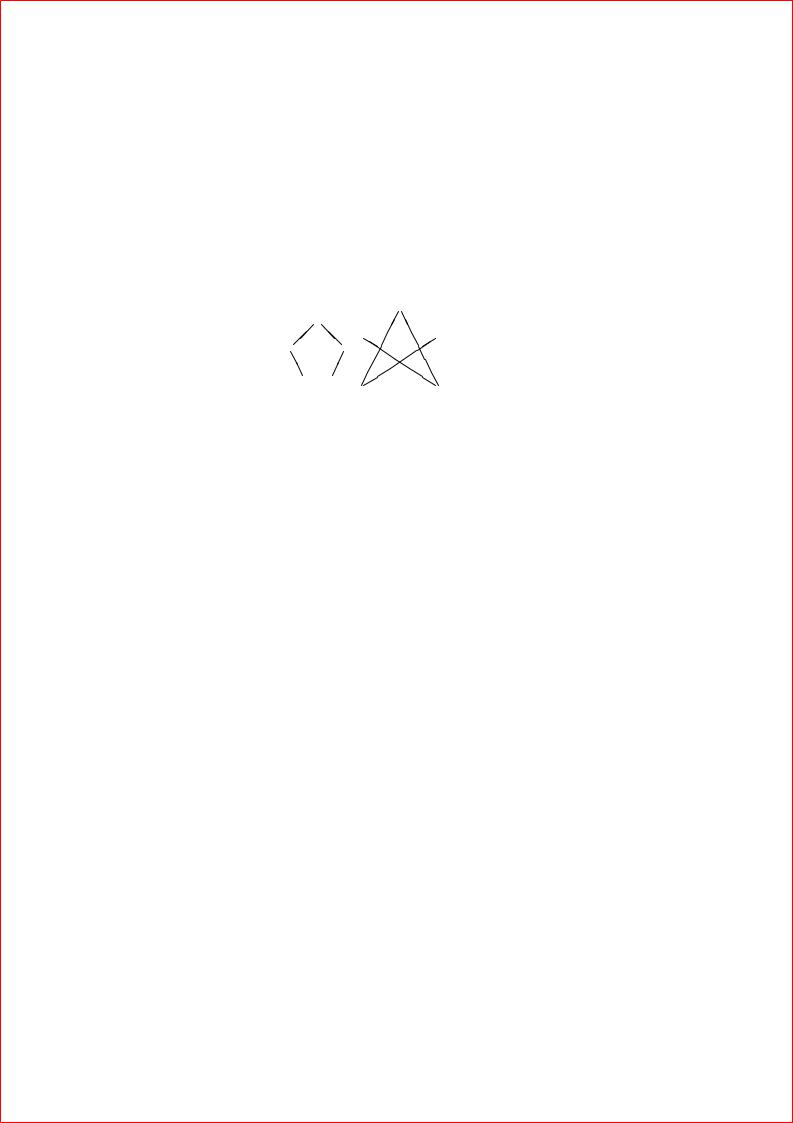
Студентка Примерная нарисовала две красивых диаграммы Гес-

се:

·

·

·

·

·

·

·

·

·

·

Какую ошибку содержат эти диаграммы и какую из них можно

упростить после исправления ошибки любым способом?

5.3.11.

Студент Лыцаренко защитил студентку Примерную, заявив, что

это —

диаграммы для предупорядоченных множеств. Насколько

обоснована его защита?

5.3.12.

Определение 5.3.9 содержит неточность. Найдите ее и исправь-

те.

5.3.13.

Не ошибся ли автор в определении максимального элемента, опу-

стив условие y 6= x0? А как для предупорядоченных множеств?

5.3.14.

Переведите на формальный язык следующее определение:

Отношение называется согласованным, если два объекта,

относящиеся к одному и тому же третьему объекту, относят-

ся между собой.

Не могли бы Вы переформулировать данное предложение на со-

держательном языке так,

чтобы оно, не изменив математического

смысла, стало бы легче понимаемым?

§ 5.4.

ФУНКЦИИ

Поэтому соответствия, для которых x X 1 y Y (x, y) R, назы-

вают функциональными. Часто функциональные соответствия отожде-

ствляются с функциями, но такое отождествление не всегда правомер-

но даже в классической математике (в частности, в областях, базирую-

щихся на теории категорий). Другое дело, что любое соответствие фор-

мы R = {(x, y)|y = f(x)} является функциональным, и в математи-

ке очень стараются, чтобы по любому функциональному соответствию

можно было определить функцию29. Если же мы интересуемся вычи-

слимостью либо определимостью, то на первый план решительно вы-

ходит первая составляющая понятия функции —

наличие правила.