
Непейвода. Прикладная логика
.PDF
4.6. ПРОСТЕЙШИЕ ПРЕОБРАЗОВАНИЯ |
71 |
Когда мы переходим к формализации, нужно строжайше следить за един- |
|
ством контекста (классическая логика предполагает его постоянство и, |
|
более того, является той логикой, которую мы практически вынужде- |
|
ны использовать в случае формализации знаний в постоянном контек- |
|
сте.) Поэтому после перевода формального предложения на обычный |
|
язык полученную формулировку целесообразно отредактировать с уче- |
|
том возможных изменений контекста. Преимущество, которое мы полу- |
|
чаем, проводя дополнительные преобразования, огромно по сравнению |
|
с некоторыми неудобствами: вылавливаются все те места, где в содер- |
|
жательном рассуждении контекст потихоньку подменяется. |
|
Еще одним важным приложением наших тавтологий является свой- |
|
ство замены эквивалентных. Подробнее оно будет разобрано в следу- |
|
ющей части, а сейчас его можно охарактеризовать как разрешение ис- |
|
пользовать в любом месте вместо логического выражения другое, экви- |
|
валентное ему. |
|
И наконец, приведем важное эквивалентное10 преобразование им- |
|
пликаций. Очевидно, что A B и B A — |
разные утверждения. А |
если включить сюда еще и импликации между отрицаниями? Тавтоло- |
|
гия 4.49 показывает, что ¬B ¬A то же самое, что и A B. |
|
Упражнения к § 4.6 |
|
4.6.1. Для всех упражнений на перевод с естественного на формальный |
|
и обратно, которые Вы решали и будете решать, запишите отри- |
|
цание соответствующих формул. |
|
4.6.2. Проверьте на таблицах истинности, тавтологии ли следующие фор- |
|
мулы: |
|
|
1. |
(A B) (A C) (A B C); |
|
|
2. |
((A B) C) (A (B C)); |
|
|
3. |
((A B) & (C D)) ((A C) (B D)). |
|
4.6.3. |
Запишите все возможные импликации между A, B и их отрица- |
||
|
ниями и установите, какие из них эквивалентны друг другу. |
||
4.6.4. Постройте таблицу истинности для формул ¬(A B) и |
¬(A |
||
|
B) и дайте правила формулировки отрицаний для и . |
|
|
10 В традиционной классической логике. В неклассических оно почти всегда исчезает.

72 ГЛАВА 4. МЕТОДЫ ПЕРЕВОДА
Дайте формулировки отрицаний для и и на их основе 4.6.5. выберите одну из формулировок11. (4.19) (4.59)
Запишите содержательное предложение соответствующее отри
4.6.6. цанию формулы (4.24). , -
11 В данном случае мы сталкиваемся еще с одним принципом успешной формализа ции не говорите лишнего Если утверждения уже стали истинными в ситуациях име- ющихся: в виду сначала попытайтесь. поработать с ними и добавляйте новые лишь, при- необходимости,. ,

Глава Базовые математические5. понятия
Данная глава посвящена введению в использование базисных понятий современной математики несколько выходящих за рамки чистого языка логики множеств отношений, функций Она содержит также краткое введение: в язык диаграмм, и стрелок, столь. же органичный для функций сколь органичен язык логики для высказываний, . ,
§ 5.1. МНОЖЕСТВА. |
|
ДИАГРАММЫ ЭЙЛЕРА И ВЕННА |
|
В современной математике понятие множества является одним из цен- |
|
тральных и окутанных наибольшим числом предрассудков. Множества |
|
являются прежде всего удобным средством превращать высказывания в |
|
объекты и, соответственно, операции над высказываниями в функции. |
|
При этом классическая логика переходит в булеву алгебру. Лучше все- |
|
го охарактеризовать множество как “ единое имя для совокупности всех |
|
объектов, обладающих данным свойством.” Но это предложение, конеч- |
|
но же, не может считаться определением. |
|
Множество всех объектов, обладающих свойством A(x), обознача- |
|
ется {x | A(x)}. Если Y = {x | A(x)}, то |
A(x) называется характери- |
стическим свойством множества Y , а Y — |
сверткой предиката A. По |
определению Y , выполнена следующая эквивалентность: |
|
y(y Y A(y)). |
|
Два множества считаются равными, если их характеристические свой- |
|
ства эквивалентны1. (Часто это выражают словами: «Множества равны, |
|
1 Как мы уже замечали, если математики уславливаются считать некоторые объек-

74 |
|
|
|
|
ГЛАВА 5. |
БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ |
||
если они содержат одни и те же элементы».) Множество X вложено в |
||||||||
множество |
Y (X |
|
Y ), |
если |
характеристическое свойство Y следует из |
|||
|
|
|
2 3 |
. Поскольку |
||||
характеристического свойства X |
|
|||||||
|
|
|
(A B) (A B) & (B A), |
|||||
X Y |
и Y X тогда и только тогда, когда X = Y . |
|||||||
Простейшее из множеств, и чаще всего встречающееся в форму- |
||||||||
лах, — |
пустое множество , |
вообще не содержащее элементов. Очевид- |
||||||
но, что пустое множество задается тождественно ложным характери- |
||||||||
стическим свойством, и соответственно все пустые множества равны. |
||||||||
Поэтому считается, что множество квадратных кругов равно множеству |
||||||||
удмуртов-негров. Но здесь, как и всегда, когда математика расходится со |
||||||||
здравым смыслом4, возникают некоторые тонкости. |
||||||||
Было бы естественно, чтобы тождественно истинное условие, на- |
||||||||
пример x = x, определяло “ полное” множество. Но математики давно |
||||||||
уже отказались считать, что существует единое такое полное множество |
||||||||
для всех разделов математики, не говоря уже о ее применениях. Тут |
||||||||
вступает в свои права контекст, и мы вспоминаем о том, что неотъем- |
||||||||
лемым элементом математической интерпретации является универс — |
||||||||
множество всех рассматриваемых в данной теории предметов. Очевид- |
||||||||
ты равными, то тем самым они отказываются рассматривать какие-либо их свойства, |
||
нарушающие равенство. Таким образом, отождествив два множества, характеристиче- |
||
ские свойства которых эквивалентны, мы тем самым косвенно заявляем, что, во-первых, |
||
элементы во множествах совершенно равноправны, поскольку единственное свойство |
||
элемента, принимаемое во внимание при образовании множества — |
характеристиче- |
|
ское; во-вторых, элементы не повторяются. Значит, при реализации, скажем, машинной |
||
структуры данных, соответствующей множествам, нужно как-то учесть эти свойства, а |
||
это порою не так-то просто. Например, задав множество просто как массив переменной |
||
длины из элементов, мы грубо нарушаем оба требования: элементы становятся упоря- |
||
доченными согласно индексам, и в массиве могут попасться одинаковые члены. |
||
2 Порою значок |
используют лишь для т. н. строгого вложения, когда вдобавок вы- |
|
полнено X 6= Y , а наше вложение обозначают . Но посмотрите, как уродливо выража- |
||
ется строгое вложение, и станет ясно, что лучше брать за исходное нестрогое вложение, |
||
что и ввел в математическую традицию Никола Бурбаки. |
|
|
3 Никола Бурбаки — |
легендарный современный математик (легендарный как в смысле |
|
основательности его работ так и в буквальном Его на самом деле никогда не суще ствовало под этим именем, выпускала серию работ.) группа выдающихся математиков- французской, школы (не говорим французов, потому что в их числе был поляк).
4 Но и когда она с ним согласуется, часто все не так просто. . .

5.1. МНОЖЕСТВА |
75 |
но, что тождественно истинное условие определяет универс, и тожде- |
||
ственно истинные формулы, относящиеся к разным теориям, определя- |
||
ют разные универсы. |
|
|
В математике рассматривается одна теория — теория множеств, |
||
которая длительное время претендовала на выразимость в ней всех ма- |
||
тематических понятий. В ней пытаются базироваться на одних лишь |
||
множествах, и тогда ее универс должен быть множеством всех мно- |
||
жеств. Но выяснилось, что принятие существования множества всех |
||
множеств приводит к невозможности совместить некоторые построе- |
||
ния, принятые в математике, в рамках одной теории. Так, например, од- |
||
на из аксиом теории множеств: |
если X — |
множество, то для любого |
условия A {x | x X & A(x)} — |
также множество. Приняв существо- |
|
вание множества всех множеств, мы при помощи данной аксиомы вы- |
||
деляем из него расселовское множество из примера (1.7), которое при- |
||
водит к парадоксу. Оно определяется как |
|
|
{x | x U & x / x} |
||
(как обычно, U — универс). |
|
Математики вышли из данного положения, как всегда, с честью, но |
|
не без потерь и хитростей: было просто принято, что множества всех |
|
множеств нет, и универс теории множеств сам множеством не является5. |
|
Примененный метод лечения полностью соответствует тому, как дей- |
|
ствуют представители других наук в случае появления противоречий в |
|
парадигме. |
совокупность взглядов и понятий, кото- |
Парадигма — |
|
рые считаются принадлежащими данной науке.
Она автоматически отбрасывает и те взгляды которые ей противоречат как ненаучные и те понятия которые в нее, не входят как тоже не научные( либо не), принадлежащие, данной специальности (и потому не- интересные Парадигмой пользуются пока она совсем не износится- и зачастую )она. уже трещит по всем швам, а на нее упорно ставят за, платки Одним из видов таких заплаток является, убийство факта про-
. , -
5 Впрочем американский логик Куайн предложил вариант теории множеств в кото ром прекрасно, уживаются с множеством всех множеств но как и следовало ожидать, - эта теория множеств показалась несколько странноватой,в других, отношениях и не бы, ла воспринята математиками. -

76 ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
тиворечащего парадигме, путем вывода данного понятия за ее преде- |
||
лы либо переформулировки соответствующего термина таким образом, |
||
чтобы он устранял выявленный недостаток. Другой способ — |
постули- |
|
рование данного факта как нового принципа6. Так, геологи длительное |
||
время отбрасывали как противоречащую парадигме теорию движения |
||
материков, предпочитая каждый конкретный факт либо игнорировать, |
||
либо объяснять по отдельности. Математики по крайней мере потру- |
||
дились свести спасенные после заплаток принципы теории множеств в |
||
достаточно стройную систему. |
конечного числа элементов a1, |
|
Множество, состоящее из |
. . . , an, |
|
принято обозначать {a1, . . . , an}. Его определение через характеристи- |
||
ческое свойство: |
|
|
{a1, . . . , an} = {x | x = a1 · · · x = an} . |
(5.1) |
|
Исходя из тождества 5.1, можно видеть, в частности, что |
|
|
{a, b} = {b, a}, {a, a} = {a}.
Стоит отметить еще одну тонкость. Нужно строго различать x и {x}. |
|||||||||
Первое выражение обозначает сам элемент, а второе — |
множество, за- |
||||||||
ключающее этот один элемент. Разница между ними примерно такая же, |
|||||||||
как между шимпанзе и шимпанзе |
, |
посаженным в |
клетку в зоопарке: |
{ |
x |
} |
|||
|
|
7 |
|
|
|
||||
скорее похоже на такую клетку, чем на ее обитателя |
|
. |
|
|
|
|
|||
Операциям конъюнкции и дизъюнкции над формулами соответству- |
|||||||||
ют операции пересечения ∩ и объединения множеств: |
|
|
|
|
|||||
4 |
|
4 |
|
|
|
|
} , |
|
|
X Y = {x | x X y Y } |
|
X ∩ Y = {x | x X & y Y |
|
||||||
а операцию, соответствующую отрицанию, как правило, вводят лишь
6 Не важно что он как правило не согласуется с другими На много шагов вперед неприятные вещи, никто, продумывать, не любит. !
7 Конечно же множество в некотором смысле изоморфно т е имеется взаимно однозначное отображение, , сохраняющееX все основные структуры( .) множеству. -
{{x} | x X} .
Но насколько такой изоморфизм может быть коварным видно из того что в теории множеств Куайна где существует универс его часто нет ,Так что одно найдешь, другое потеряешь. . . ( ) . ,

5.1. МНОЖЕСТВА |
|
|
77 |
||||
тогда, когда фиксирован универс U. Дополнение X множества X — |
это |
||||||
|
|
|
|
¯ |
|
|
|
множество элементов U, не входящих в X8. |
|
|
|
||||
|
Говорят, что два множества не пересекаются, если их пересечение |
||||||
— |
пустое множество: |
|
|
|
|||
|
|
|
|
X ∩ Y = . |
|
|
|
|
Объединение, пересечение и дополнение обычно называются буле- |
||||||
выми операциями, составленные из множеств с их помощью выраже- |
|||||||
ния — |
булевыми выражениями, значение такого выражения |
— |
булевой |
||||
комбинацией входящих в него множеств, а равенства двух булевых вы- |
|||||||
ражений — |
булевыми тождествами (например, X X = X). Через |
||||||
булевы операции определяются еще две полезные операции над мно- |
|||||||
жествами — |
разность X \ Y = (X ∩ −Y ) и симметрическая разность |
||||||
X4Y = (X \ Y ) (Y \ X). Булевы тождества позволяют продемон- |
|||||||
стрировать достаточно уникальный пример превращения иллюстраций |
|||||||
в строгие доказательства. Он интересен еще и как пример представле- |
|||||||
ния данных: таблица истинности превращается в совершенно непохо- |
|||||||
жую внешне, но изоморфную ей структуру. |
|
|
|
||||
|
В |
XVIII веке Л. Эйлер использовал для иллюстрации взаимосвязей |
|||||
между понятиями чертежи, которые были названы позднее |
«круги Эй- |
||||||
лера» (точнее, как мы и будем называть их, “ диаграммы Эйлера”). |
На- |
||||||
пример, соотношение между понятиями “ протестант, католик, христи- |
|||||||
анин, |
европеец” показывает диаграмма 5.1. |
|
|
|
|||
|
Здесь не имеет значения относительный размер кругов либо других |
||||||
замкнутых областей, но лишь их взаимное расположение. Безусловно, |
|||||||
такие диаграммы могут играть в логике лишь ту же роль, |
что черте- |
||||||
жи в геометрии: они иллюстрируют, помогают представить и доказать, |
|||||||
но сами ничего не доказывают. Учитывая, что по сути своей логика не |
|||||||
является математической наукой и поэтому имеет дело с понятиями, а |
|||||||
не с терминами, часто диаграммы Эйлера являются оптимальным сред- |
|||||||
ством. Но для математических понятий и булевых операций из них мож- |
|||||||
но вывести другой вид диаграмм, когда чертеж становится строгим до- |
|||||||
казательством9. |
|
|
|
||||
|
|
|
|||||
8 |
Таким образом, в теории множеств дополнений у множеств нет; но о них, тем не ме- |
||||||
нее, говорят, имея в виду дополнение до фиксированного подразумеваемого множества, |
|||||||
например, некоторого множества действительных чисел до всего R. |
|
|
|
||||
9 |
Этот вид диаграмм предложил и детально разработал Дж. Венн, поэтому они назы- |
||||||
ваются по его имени: диаграммы Венна. |
|
|
|
||||
78 ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Католики |
|
Христиане |
Европейцы |
Протестанты |
|
Рис. 5.1: Диаграмма Эйлера
Следующие |
две |
диаграммы |
||
показывают, |
что |
|
тождество |
|
не выполнено. Объединение |
||||
областей, |
помеченных |
, |
||
соответствует левой и правой |
||||
частям тождества, |
соответ- |
|||
ственно. |
|
|
|
|
X* *Y |
X* *Y |
*
* *
Z Z
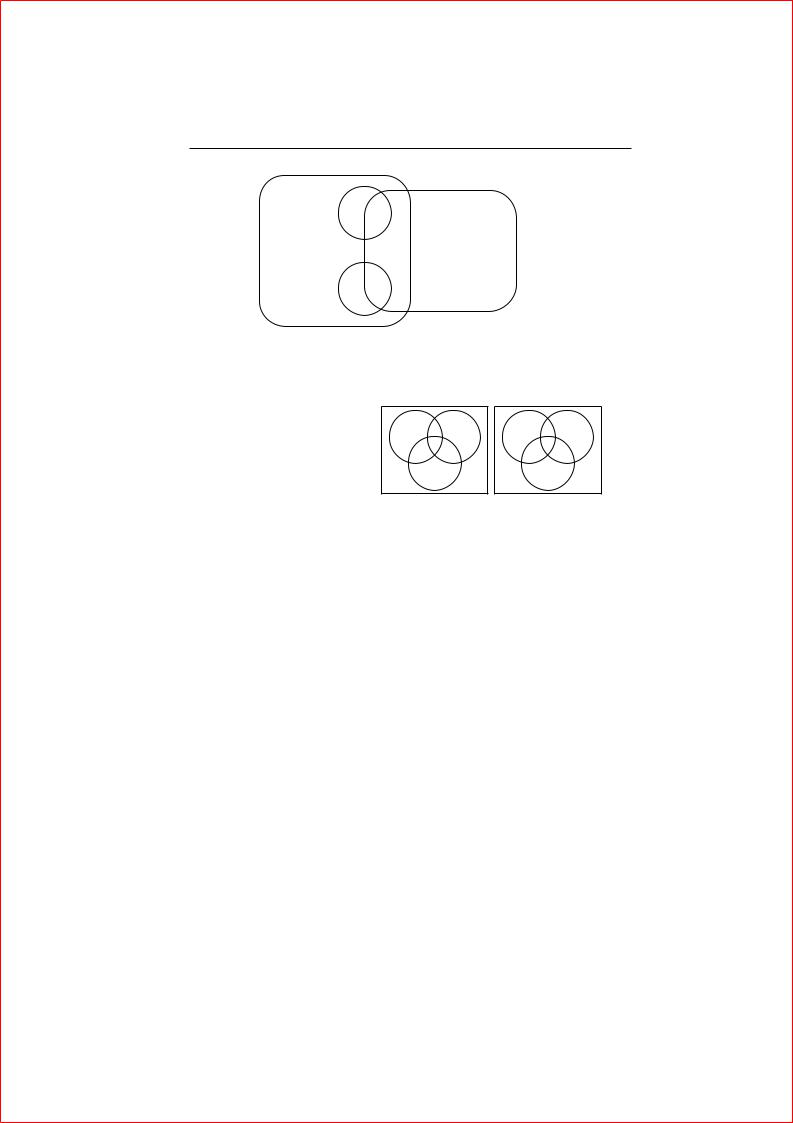
Рис. 5.2: Правильная диаграмма Венна
Начнем с примера. Рассмотрим тождество X 4(Y 4Z) = (X Y |
|
Z) \ ((X ∩ Y ) (X ∩ Z) (Y ∩ Z)). Левой и правой его частям можно |
|
сопоставить следующие чертежи (см. рис. 5.2). |
|
Квадрат изображает универс, круги — |
наши множества. Из их рас- |
смотрения видно что выражение в левой части совпадает с выражением в правой Более того, интуитивно очевидно что данный чертеж на са мом деле. доказывает,тождество для всех возможных, множеств -
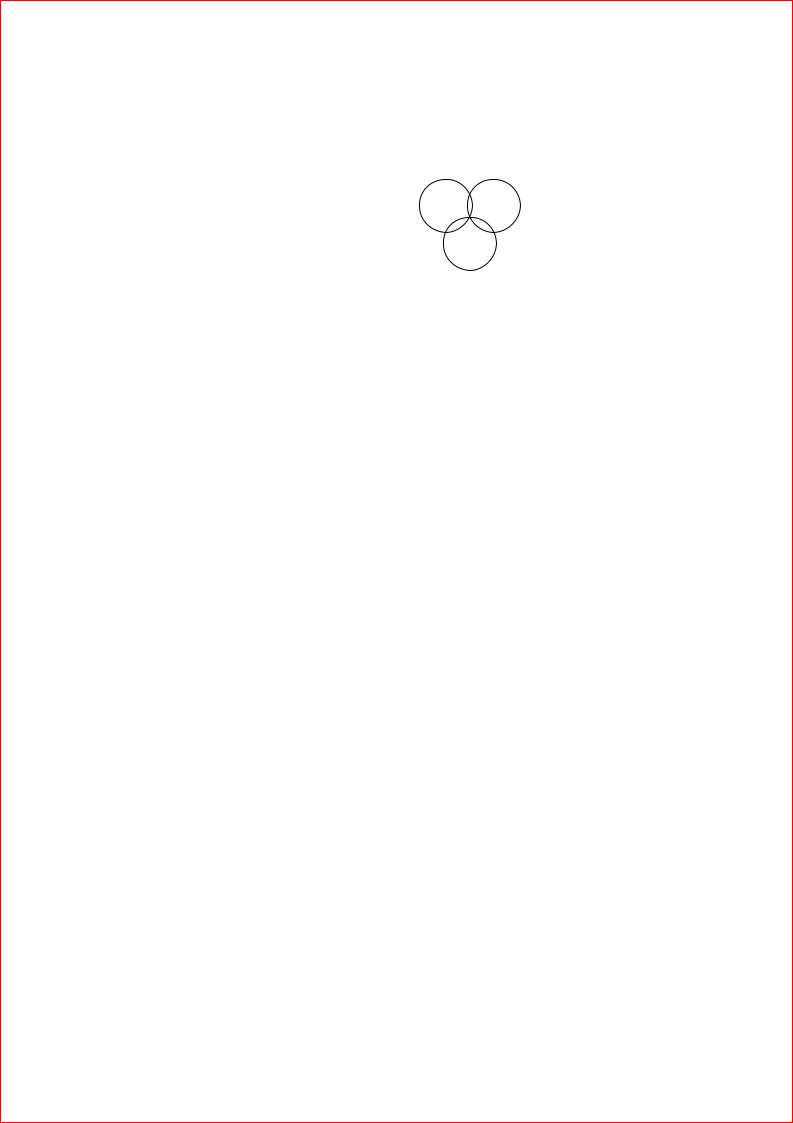
Если же нарисовать диаграмму чуть чуть неаккуратно некоторые. области могут пропасть и проверка соответственно- оказывается, из лишне оптимистичной см рис , , -
Для того чтобы установить( . точный. 5.3). критерий удовлетворительности чертежа рассмотрим соотношение между булевым тождеством и логи ческой формулой, Каждому булеву выражению над множествами сопо- ставляется логическая. формула в которой заменяется на на-
на на Два множества, равны когдаX соответствующиеc имX, фор∩ мулы&, эквивалентны, − ¬. . А для проверки эквивалентности, нужно построить-
5.1. МНОЖЕСТВА |
79 |
|
|
* |
* |
Самая внутренняя область пропала, и |
X |
Y |
|
|
* |
||
кажется, что рассматриваемое тожде- |
|
Z |
|
ство выполнено. |
|
||
Рис. 5.3: Неправильная диаграмма Венна |
|||
таблицу истинности. В этой таблице вычисляются значения формул, со- |
|||
ответствующих двум частям равенства, при всех возможных комбина- |
|||
циях значений элементарных подформул. Проанализируем, чему соот- |
|||
ветствует такая комбинация на языке теории множеств. Если есть си- |
|||
стема множеств Xi, то задание значений формул c Xi соответствует |
|||
указанию для всех Xi, чему именно, множеству либо его дополнению, |
|||
принадлежит c. Это приводит к следующим определениям. |
|||
Определение 5.1.1. Составляющие системы множеств {X1, . . . , Xn} |
|||
задаются следующим индуктивным определением. |
|
||
Базис. Составляющие {X1} суть само X1 и его дополнение. ¯ |
|||
Шаг. |
Если S — |
составляющая {X1, . . . , Xn−1}, то S∩Xn и S∩ Xn — |
|
составляющие {X1, . . . , Xn}. |
|
||
Система множеств независима, если все ее составляющие непусты. |
|||
Теорема 5.1. .(Венн) Если булево равенство выполнено для некоторой |
|||
независимой системы множеств, то оно выполнено для любой системы |
|||
множеств. |
Прежде всего отметим, что любая составляющая S |
||
Доказательство. |
|||
системы |
{X1, . . . , Xn} однозначно определяет значения всех формул |
||
вида c Xi. Это легко устанавливается по индукции. Отсюда следует, |
|||
что две составляющие либо совпадают, либо не пересекаются. Далее, |
|||
если Y — |
булева комбинация {X1, . . . , Xn}, S — |
составляющая этой |
|
системы, то S либо подмножество Y , либо не пересекается с Y . Это вы- |
|||
текает из того, что значение характеристического свойства Y полностью |
|||
определяется значениями всех c Xi. И наконец, |
составляющая неза- |
||
висимой системы является подмножеством тогда и только тогда когда соответствующее значение в таблице истинностиY формулы определяю,
щей есть Значит в независимой системе любая булева,комбинация- однозначноY , разлагается1. , на составляющие т е представляется как объ единение составляющих) и это разложение( . сохраняется. и для других-

80 ГЛАВА 5. БАЗОВЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
систем множеств (конечно, для зависимых систем могут появиться и |
|||||||
другие разложения). Поэтому если в независимой системе две булевы |
|||||||
комбинации имеют одни и те же составляющие, они будут иметь одина- |
|||||||
ковые значения и в любой другой системе. |
|
||||||
Итак, булево равенство достаточно проверить на одной, но хорошо |
|||||||
подобранной системе множеств. |
Следовательно, правильно нарисован- |
||||||
ная диаграмма Венна полностью обосновывает тождество. |
|
||||||
Диаграммы Венна подводят нас к следующему фундаментальному |
|||||||
вопросу. |
В них нет предложений, нет правил вывода, не видно умоза- |
||||||
ключений. Так что же такое доказательство с математической точки зре- |
|||||||
ния? Ответом на это может быть следующая характеризация: |
|
||||||
|
|
Доказательство — |
конструкция, синтаксическая |
|
|||
|
|
правильность которой гарантирует семантиче- |
(5.2) |
||||
|
|
скую. |
|
|
|
|
|
Не известно ни одного случая, когда такое описание отказало бы10. И |
|||||||
заодно данная формулировка показывает, насколько далеко нынешним |
|||||||
программам до доказательств: в программе синтаксическая правильность |
|||||||
ничего не гарантирует. |
|
|
|
|
|||
В заключение отметим, что множество всех подмножеств данного |
|||||||
множества X называется его множеством-степенью и обозначается 2X |
|||||||
либо P X. |
|
|
|
|
|||
Упражнения к § 5.1 |
|
|
|
|
|||
5.1.1. |
Независима ли следующая система множеств: |
|
|||||
|
|
|
|
X |
Y |
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
||||
5.1.2. |
Мы научились проверять на диаграммах булевы равенства. А как |
||||||
|
с булевыми вложениями (утверждениями формы X Y, где X и |
||||||
|
Y — |
булевы выражения)? |
|
|
|
||
10 С точки зрения любой науки кроме математики это не просто характеристика а полноправное определение Но в, математике само понятие, определения превращено, в термин и, соответственно, несколько. подменено (см. главу 12).
