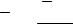9

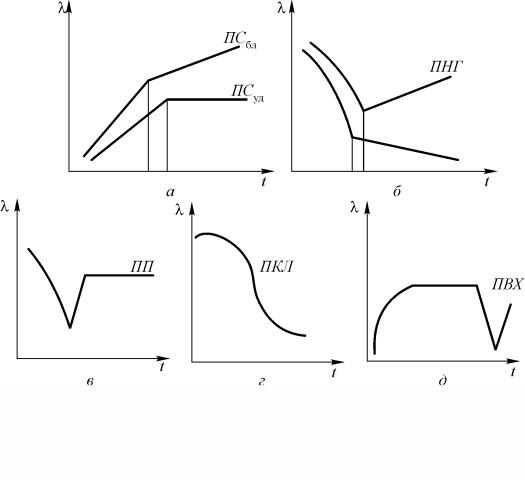
Якщо відомо об’ємну масу матеріалу ρ, можна визначити питому теплоємність за формулою

Сp = аλρ.

Характер залежності теплопровідності від температури для деяких полімерних матеріалів подано на рис. 10.2.

Рис. 10.2

Для кристалічних полімерів у твердій фазі теплопровідність значно вища, ніж для аморфних, і зменшується з підвищенням температури. Теплопровідність аморфних полімерів збільшується з підвищенням температури. В області переходу з твердого стану в розплав теплопровідність кристалічних полімерів різко спадає. Щодо аморфних полімерів відбувається зміна нахилу прямої λ = f (t). Теплопровідність розплавів полімерів незначно залежить від температури і майже не залежить від тиску.

Усі ділянки кривих λ = f (t) можна описати рівнянням

λt = a+bt,

де а, b мають різні значення для твердого тіла і розплаву кожного полімеру. Значення λ для полімерів (термопластів) змінюється в межах

0,11…0,33 Вт/(м · °С.).

181

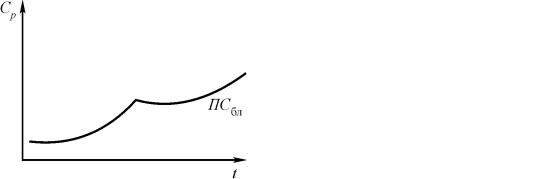
Питома теплоємність кристалічних полімерів зростає спочатку незначно з підвищенням температури, а потім утворює пік в області фазового переходу. В області температур розплаву питома теплоємність наближається до початкової за температури 20 °С і майже не змінюється з температурою (рис. 10.3). Незначне підвищення тиску трохи зменшує питому теплоємність. Питома теплоємність аморфних полімерів плавно зростає зі збільшенням температури, створюючи злам на кривій в області, що відповідає переходу в розплав. Причому, теплопровідність твердої фази зростає швидше, ніж теплопровідність розплаву (рис. 10.4).

Із графіків залежності Cp = f (t) випливає висновок, що нагрівання до температури розплаву кристалічних полімерів потребує значно більше енергії порівняно з аморфними, і близько половини цієї енергії витрачається на руйнування кристалічної структури полімерів.

Температуропровідність аморфних полімерів суттєво не залежить від тиску, а залежно від температури всі отримані експериментальні дані можна описати рівнянням прямої:

де С, d — коефіцієнти, отримані в результаті обробки результатів експерименту методом найменших квадратів (рис. 10.5). Для кристалічних полімерів у твердій фазі характерне зменшення температуропровідності з підвищенням температури. У зоні фазового перетворення коефіцієнт а у 15—20 разів менший, ніж за температури 20 °С. Після переходу полімера в розплав а різко збільшується до значень, близьких до початкових, і лінійно слабко спадає з підвищенням температури. Тиск збільшує температуропровідність для твердих кристалічних полімерів і на 2…5 °С підвищує температуру фазового переходу полімера в розплав. В області розплаву тиск помітно впливає на температуропровідність (рис. 10.6).

182

Розв’язок диференціальних рівнянь для тіл різної форми можна одержати у вигляді залежностей:

— для пластини

де µn — корені характеристичних рівнянь для кожного виду виробів. Отримані розв’язки можна використати для розрахування часу

охолодження полімерних ниток, прутків, листів, плівок (плоских) і гранул кулястої форми. Однак теплофізичні властивості полімерних матеріалів з моменту їх завантаження в машину до одержання готових виробів (у діапазоні температур переробки) різко міняються. Щоб використовувати рівняння (10.14)—(10.16), потрібно визначити середньоінтегральні значення температуропровідності і теплопровідності в діапазоні температур переробки. Як такий діапазон вибирають перепад температур на виході з формувальної головки і на виході із зони охолодження.

Середньоінтегральні значення ап та λп можна знайти методом графічного інтегрування чи за допомогою формули Сімпсона

тивостей на вісь Х.

10.3.1. Проектний розрахунок охолодного пристрою

Розрахунок полягає у визначенні часу охолодження виробу. У ньому задано: вид і геометрію виробу; температуру на виході з формувального інструмента tп; місце виробу в просторі; відповідну кінцеву температуру виробу tк; температуру охолодного середовища tрід = const; інтенсивність охолодження чи вид теплообміну — α; теплофізичні властивості полімерного виробу.

184

Щоб установити час охолодження, доцільно визначити, дотримуючись такої послідовності:

— безвимірну температуру

θ= tк −tpід ; tп −tрід

— критерій Біо

де l — визначальний розмір, що дорівнює половині товщини щодо листа і плоскої плівки, l = δ; для ниток, прутка і гранул дорівнює радіусові виро-

бу, l = R;

— критерій Фур’є з допомогою графоаналітичних залежностей (10.13);

— час охолодження

τ = Fol2 ;

an

—довжину охолодної ділянки L за відомими τ і швидкістю одержання полімерного виробу V:

L= Vτ.

10.3.2.Перевірний розрахунок охолодного пристрою

Задано ті самі величини, що й у попередньому випадку, крім кінцевої температури полімеру tk та довжини охолодної ділянки. Останню задано додатково, тому що відомо потрібний час охолодження τ. Для встановлення кінцевої температури полімерного виробу на виході з охолодного пристрою слід визначити:

—критерій Біо за формулою (10.17);

—критерій Фур’є Fo = (an τ) / l2 ;

—безрозмірну температуру θ за графоаналітичною залежністю (10.13);

—кінцеву температуру виробу tк;

tк = tpід + θ (tп – tрід).

Для охолодження полімерних виробів застосовують воду і повітря. Причому процес охолодження може відбуватися в умовах як природної

Nu = f (Gr, Pr),

185

так і вимушеної конвекції

Nu = f (Re, Pr).

Продуктивність охолодних пристроїв, а отже, і всіх агрегатів для виробництва виробів неперервним способом, залежить від часу охолодження τ, що, у свою чергу, залежить від критерію Ві і фактично від інтенсивності тепловіддачі α. Чим вища інтенсивність тепловіддачі, тим менший час охолодження за умови, що 0,1 ≤ Ві ≤ 100.

Під час природної конвекції α збільшується разом з перепадом температур ∆t. Отже, можна швидше охолоджувати полімерний виріб холоднішою рідиною. Під час вимушеної конвекції α збільшується не тільки разом з ∆t, але й зі зростанням швидкості руху охолодної рідини чи відносного руху рідина—виріб. Однак ці залежності непропорційні і мають критеріальний вигляд.

10.3.3. Охолодження рукавної полімерної плівки

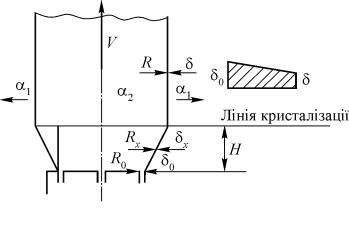
Охолодження тонкостінної рукавної плівки можна розглядати як процес, що відбувається за малих значень Ві (Ві ≤ 0,1 чи Ві→0). У цьому разі температура на поверхні плівки мало відрізняється від температури на осі плівки, тобто можна вважати, що розподіл температури по перерізу плівки рівномірний. Задача стає за визначенням зовнішньою, тому що інтенсивність зміни температури у центрі товщини плівки визначається інтенсивністю теплообміну на її поверхні.

Виходячи з припущення про сталість температури в об’ємі виділеного елемента плівки і розгляду теплового балансу цього елемента, було отримано диференціальне рівняння, що описує процес охолодження полімерної рукавної плівки:

Зогляду на те, що кількість теплоти, яка виділяється за одиницю часу

зодиниці поверхні плівки за рахунок дисипації енергії під час розтягання в’язкого полімеру qд(x, τ) і за рахунок кристалізації qкр│х=H на відстані

х= Н (від головки до лінії кристалізації), незначна порівняно із загальним

186

порівняно з іншими величинами і втрати теплоти за рахунок випромінювання малі, рівняння (10.18) можна записати в такому вигляді:

Рівняння (10.19) справедливе для зон до і після лінії затвердіння. У зоні до лінії затвердіння змінюються товщина плівки δх і швидкість руху рукава Vx. Однак рухома маса розплаву в усіх перерізах зони формування виробу постійна.

З умови сталості витрат маси розплаву в усіх перерізах і вважаючи рівними значення об’ємної маси на початку і наприкінці формування можна записати:

де R0, δ0, V0 — відповідно радіус, товщина і швидкість руху рукавної плівки на виході з головки; Rx — поточне значення радіуса.

Можна припустити, що рукав у зоні формування являє собою конус (рис. 10.7), і одержати таке співвідношення

H = R − R0 . x Rx − R

де Н — висота лінії кристалізації; β0 = R/R0 — ступінь роздування рукава.

187

Після вираження коефіцієнтів α1 та α2 через єдиний коефіцієнт α диференціальне рівняння (10.19) з урахуванням (10.20) та (10.21) матиме вигляд:

Розв’язок цього рівняння для зони до лінії затвердіння являє собою такий вираз

Для ділянки рукава вище лінії кристалізації, де не змінюється товщина плівки, розв’язок диференціального рівняння (10.22) має такий вигляд:

Тут х — відстань від формувальної головки за висотою рукава. Величину α, що входить до рівняння температурного поля, визна-

чають залежно від режиму охолодження. Якщо охолодження відбувається в умовах природної конвекції, використовують рівняння вигляду:

Nu = f (Gr · Pr).

Причому розв’зок задачі залежить від визначального розміру в критерії Грасгоффа.

Якщо охолодження відбувається завдяки обдуву рукава струменем повітря, треба використовувати таке рівняння:

Критерій Re визначають за формулою

Re = U x .

υрід

188

У формулах (10.23) і (10.24) α — середній щодо периметру коефіцієнт тепловіддачі; х — визначальний розмір; U — середня швидкість струменя:

Umax1, Umax2 — максимальні значення швидкості струменя на початку і в кінці розглянутої ділянки.

Відношення швидкостей:

де U* = 5…25 м/с — швидкість повітря в місці контакту струменя повітря з плівкою;

де К — коефіцієнт початкової турбулентності струменя, визначають експериментально; b* — ширина струменя у місці його контакту з плівкою

Формули (10.25)—(10.29), що характеризують епюру швидкостей, отримано після обробки результатів експерименту.

Останнім часом застосовують новий спосіб охолодження рукавної плівки — охолодження за допомогою стічної плівки рідини. Для визначення коефіцієнта тепловіддачі в цьому разі запропоновано таке рівняння:

Рівняння (10.30) застосовують, якщо 400 ≤ Re ≤ 300. У цьому рівнянні Nu = αδ ⁄ λ; α — коефіцієнт тепловіддачі; δ — середня товщина шару стічної рідини; λ — коефіцієнт теплопровідності рідини за середньої температури.

Критерій Re у рівнянні (10.30), що характеризує динаміку процесу стікання плівки рідини, визначають за формулою

Re = 4ГνV ,

де ГV — об’ємна маса зрошення, яку визначають за рівнянням:

189

ГV = VP ,

чи

ГV = 2Gl ,

де V — об’єм стічної плівки; Р — змочений периметр; G — витрати рідини; l — висота виробу, по якому стікає рідина.

10.3.4. Інтенсифікація процесу охолодження труб

Охолодження полімерних труб можна розглядати як нестаціонарний процес охолодження необмеженого порожнього циліндра за межових умов третього роду.

Розгляньмо необмежений порожній циліндр із радіусами R1 i R2 та початковим розподілом температур t = (r, 0) = f (r), де r — поточний радіус.

Відформована труба залишає калібрувальний пристрій і входить в охолодний пристрій, маючи рівномірний початковий розподіл температури за перерізом, тобто t0 = const. У початковий момент часу трубу розміщують в охолодному середовищі з tp < t0. Між поверхнею циліндра R = R2 і рідиною відбувається теплообмін за законом Ньютона, а внутрішня поверхня труби (R = R1) теплоізольована (межові умови другого роду). Потрібно визначити розподіл температури за товщиною труби, знехтувавши поширенням теплоти вздовж труби.

Диференціальне рівняння для розв’язання крайової задачі охолодження порожнього циліндра має вигляд

Межові умови другого роду і початкові умови мають вигляд

dt(R2 , τ) = 0; dr

t(r,0) = f (r).

Межові умови третього роду

Задачу можна розв’язати, замінивши функції t(r, τ) на надлишкову θ(r, τ), де θ = t – tрід методом власних функцій. Розв’язок набуває вигляду

190