9

Різниця між кількістю теплоти, введеною в об’єм за час dτ, і тією, яка вийшла з нього, така:

За законом збереження енергії, кількість теплоти в паралелепіпеді має дорівнювати кількості теплоти, витраченої на зміну теплоємності.

Закон теплоємності:

де ρ — об’ємна маса, кг/м3; с — коефіцієнт теплоємності, який у всіх точках тіла однаковий і не змінюється в часі, Дж/(кг°С).

Диференціальне рівняння теплопровідності в нерухомому середовищі

(7.4) дозволяє визначити розподіл температур у будь-якій точці тіла, через яку протікає теплота в результаті теплопровідності.

111

Теплофізичний комплекс, м2/с:

ρλc = a

називають коефіцієнтом температуропровідності, він характеризує теп-

лоінерційні властивості тіл, тобто здатність тіла проводити теплоту (за інших рівних умов швидше нагрівається те тіло, у якого коефіцієнт тем-

пературопровідності більший).

Якщо в процесі теплопровідності температура не змінюється залежно від часу (стаціонарний режим), то

ddtτ = 0; 0 = a 2t.

У правій частині рівняння коефіцієнт температуропровідності не може дорівнювати нулю, а отже:

Диференціальне рівняння (7.5) називають законом теплопровідності в нерухомому середовищі у сталому режимі.

Рівняння (7.4) і (7.5) визначають передачу теплоти у твердому тілі без урахування геометричних розмірів і форми самого тіла.

7.1.3.Теплопровідність плоскої стінки у сталому стаціонарному режимі

Розгляньмо плоску стінку завтовшки δ і температурою на її поверх-

нях T1 > T2 (рис. 7.6).

Розв’язавши рівняння (7.5), спрощене до

де С1 і С2 — сталі інтегрування, які можна визначити із заданих межових

Рис. 7.6 умов (умов на межі тіла):

якщо х = 0, t = T1; T1 = 0 · C1 + C2; C2 = T1; якщо x = δ, t = T2; T2 = δ·C1 + T1; C1 = T2 δ−T1 .

112

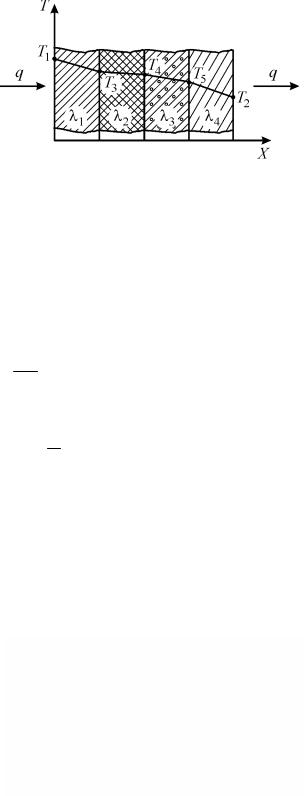
Підставляючи С1 і С2 в рівняння (7.7), одержуємо: t = T2 δ−T1 x +T1.

Визначаємо значення температурного градієнта:

Підставляємо величину температурного градієнта з виразу (7.8) у рівняння Фур’є (7.1):

Вираз (7.9) — це рівняння теплопровідності у плоскій стінці в умовах стаціонарного режиму. Рівняння (7.7) характеризує лінійний розподіл температури в плоскій стінці.

Питомий тепловий потік через плоску стінку, Вт/м2:

FQτ = q.

Термічний опір для плоскої стінки:

R = λδ.

З рівняння (7.9) маємо:

q = ∆Rt ,

де ∆t — перепад температур чи рушійна сила теплового потоку.

7.1.4. Теплопровідність багатошарової стінки

Розгляньмо тепловий потік, що протікає через стінку в стаціонарних умовах. У цих умовах тепловий потік, що протікає через багатошарову стінку, залишається постій-

ним (рис. 7.7).

Рис. 7.7

113

Запишемо потужність теплового потоку через кожну із стінок на підставі рівняння (7.11).

Q= λ1 (T1 −T3 )F;

δ1

Q= λ4 (T5 −T2 )F.

δ4

Після перетворення рівнянь та їх складання маємо:

Отримуємо рівняння теплопровідності багатошарової стінки:

Q = (T1 −T2 )F ,

∑n δi i=1 λi

де ∑n δi — сума термічних опорів.

i=1 λi

114

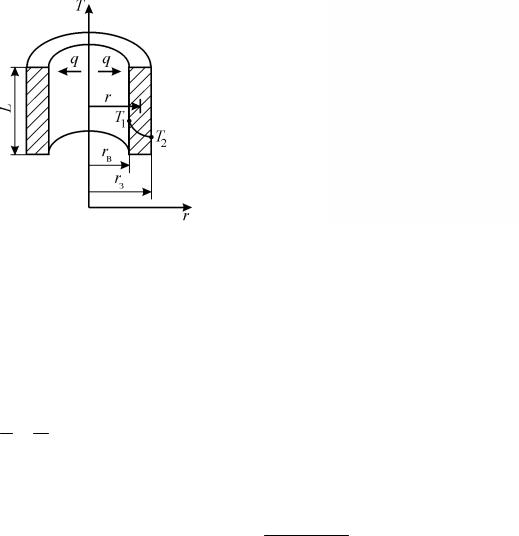
7.1.5.Теплопровідність циліндричної стінки у стаціонарному режимі

Розгляньмо формулу (7.1) для розв’язання рівняння теплопровідності циліндричної стінки

(рис. 7.8):

Q = −λ drdt 2πrL.

Розділимо змінні:

де 1 ln rз — термічний опір циліндричної стінки.

λ rв

Питомий тепловий потік, віднесений до одиниці довжини циліндричної стінки:

q = Q = 2π(T1 −T2 ) .

Потужність теплового потоку через багатошарову циліндричну стінку за аналогією з багатошаровою плоскою стінкою становить:

115

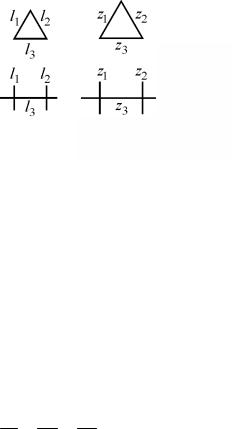
7.1.6.Основи теорії подібності і методу аналізу розмірності

Подібні явища — явища, для яких відношення схожих і характерних для них величин, постійні.

Розрізняють такі подібності: геометричну, часову, фізичну; початкових і межових умов.

Геометрична подібність встановлює, що схожі сторони певного тіла і йому подібного паралельні і їх відношення виражене сталою величиною

(рис. 7.9):

l1 = a1 — стала геометричної подібності чи масштабний множник. z1

Якщо розглянута система рухається, то геометричну подібність спостерігаємо тоді, коли всі точки системи переміщаються по подібних траєкторіях схожих точок подібної їй системи і проходять геометрично подібні шляхи.

Часова подібність встановлює, що точки чи частини геометрично подібних систем, рухаючись по геометрично подібних траєкторіях проходять геометрично подібні шляхи за проміжки часу, відношення яких стала величина:

τ1 = τ2 = τ3 = aτ — масштабний коефіцієнт часу.

τ1′ τ′2 τ′3

Фізична подібність передбачає, що в розглянутих подібних системах відношення фізичних величин у схожих точках, подібно розміщених у просторі і часі, — стала величина:

V1 = V2 = V3 = aV — масштабний коефіцієнт швидкості.

V1′ V2′ V3′

Подібність початкових і межових умов встановлює, що початкові стани на межі систем подібні. Таку подібність вважають дотриманою лише тоді, коли виконуються геометрична, часова і фізична подібності.

7.1.7. Критерії подібності й інваріанти

Якщо всі схожі величини, що визначають стан певної і подібної їй системи, виразити відношеннями, то такі відношення однорідних схожих величин називають інваріантами.

116

Інваріанти:

Інваріанти являють собою відношення простих однорідних величин. Теореми подібності. Перед дослідником фізичних явищ постають та-

кі запитання:

1.Як ставити експеримент? Що вимірювати в досліді?

2.Що робити з отриманими результатами досліду? Як їх обробляти?

3.Де можна застосувати отримані залежності?

Теорема 1 установлює зв’язок між константами подібності і дає вираз для критеріїв подібності.

Подібні між собою явища описують однаковими чи рівними за значенням критеріями подібності.

Проілюструємо першу теорему на прикладі другого закону Ньютона:

F = mVτ .

Для першої і другої, їй подібної системи, запишемо:

Відношення фізичних величин першої і другої систем позначимо інваріантами:

Із значень інваріантів отримуємо:

F1 = F2·iF; m1 = m2·im; V1 = V2·iV; τ1 = τ2·iτ.

Підставивши ці значення у вираз (7.11), отримуємо:

Порівнюючи вирази (7.11) і (7.12), робимо висновок, що вони можуть бути рівні тільки за умови, якщо

117

або

Такий комплекс фізичних величин називають критерієм подібності:

Вираз (7.13) являє собою критерій Ньютона.

Інженерний висновок з першої теореми: вимірювати потрібно фізичні величини, що входять у критерій подібності. У наведеному прикладі вимірюємо силу, час, масу і швидкість.

Теорема 2 відповідає на запитання, як обробляти експериментальні дані. Вона встановлює можливість подання диференціального рівняння у вигляді залежності між критеріями, отриманими з цього диференціального рівняння.

Будь-яку залежність між змінними, що характеризує будь-яке явище, можна подати у вигляді залежності критеріїв подібності.

Функція (7.14) — критеріальне рівняння, яке описують критеріями

k1, k2, k3, k4.

Визначальні — це критерії, які складаються з відомих, табличних фізичних величин, визначувані — це критерії, у які входить невідома фізична величина. Функцію (7.14) можна подати у вигляді:

k1 = f(k2, k3, k4).

де k2, k3, k4 — визначальні критерії; k1 — визначуваний.

Інженерний висновок з другої теореми: отримані залежності треба подавати у вигляді критеріїв подібності чи критеріальних рівнянь.

Теорема 3 відповідає на запитання, які умови неодмінні і достатні для подібності.

Подібні ті явища, умови однозначності яких подібні і визначальні критерії, складені з цих умов однозначності, чисельно рівні.

Інженерний висновок з третьої теореми: отримані залежності можна застосувати для реальних процесів, дотримуючись початкових, межових умов, геометричної і фізичної подібностей, а також часової подібності.

118

Теорема 4 (π-теорема). Вивчаючи складні явища і процеси (приклад, життєдіяльність людини), що залежать від великої кількості факторів, не можна скласти систему диференціальних рівнянь, що описують явище чи процес, однак, передбачувані фактори, які впливають на це явище, ми можемо виділити і позначити їх розмірність. Щоб відшукати залежність між виділеними факторами й описуваним явищем, використовують теорію розмірностей, в основу якої покладено π-теорему.

Загальну функціональну залежність, що зв’язує між собою n величин з m основними одиницями розмірностей, можна подати у вигляді залежності між (n – m) безрозмірними комплексами, складеними з цих величин.

Наприклад, вивчаємо фізичне явище, яке можна характеризувати п’ятьома фізичними величинами у вигляді функції:

f (α, µ, γ, c, p) = 0,

де n = 5 — зазначені фізичні величини; [L, M, T] — основні одиниці розмірностей у цих п’яти фізичних величинах, m = 3.

На основі π-теореми кількість безрозмірних комплексів дорівнює: n – m = 5 – 3 = 2. Тоді зведену загальну функціональну залежність можна подати у вигляді функції: φ(π1; π2) = 0.

Розгляньмо залежність між чотирма величинами: f (α, β, γ, τ) = 0.

Якщо всі величини (7.15) виражено в одній системі, то таку функціональну залежність можна подати у вигляді ступеневої залежності:

де x, y, z — невідомі показники степеня.

Нехай кількість основних одиниць розмірностей m = 3 [L, T, M], тоді кожна з фізичних величин має розмірність:

α=[LaT b M c ];

β=[LkT eM l ]; γ =[LoT p M q ];

τ=[LtT g M i ].

119

Підстановка розмірностей у степеневу залежність (7.16) дає:

[LaT b M c ] =[LkT e M l ]x[LoT p M q ]y [LtT g M i ]z ,

або

LaT b M c = Lkx+oy+tz T ex+py+gz M lx+qy+iz .

Порівнюємо степені за однакових одиниць розмірностей:

a = kx + oy + tz;b = ex + py + gz;c = lx + qy + iz.

Урезультаті розв’язання цієї системи знаходимо значення:

х= А; у = B; z = С й записуємо рівняння (7.16) у вигляді:

α = βAγBτC .

Тоді згідно з π-теоремою, має утворитися один безрозмірний комплекс (оскільки n – m = 4 – 3 = l):

α=1.

βAγBτC

Цей комплекс являє собою критерій подібності.

Якщо різниця n – m дорівнює нулеві чи менша за нуль, то аналіз розмірностей неможливий і потрібно переглянути кількість факторів, що впливають на явище, або в результат мають увійти інші комбінації величин.

7.2. Передача теплоти конвекцією

Передача теплоти конвекцією полягає в тому, що в рухомому шарі рідини чи газу, що прилягає до стінки, унаслідок течії стикаються зі стінкою все нові об’єми рідини, які або відносять теплоту від стінки, або приносять теплоту до стінки. Такий перенос теплової енергії в рідинах чи газах називають конвективним, а явище переносу теплоти рідинами чи газами — конвекцією.

Розрізняють вільну і вимушену конвекцію. Вільна (природна) — перенос теплоти, зумовлений вільним переміщенням рідини в результаті різниці об’ємних мас у різних точках середовища, зумовленої різницею температур, а також броунівський рух за рахунок збільшення міжмолекулярних відстаней у рідині й газі. Вимушена конвекція — перенос теплоти, коли рух зумовлений зовнішніми силами.

120