19. Задача Лагранжа на условный экстремум при дифференциальных связях.

50. Система уравнений Эйлера – Лагранжа при дифференциальных связях.

Утверждение теоремы 1 (из 18 вопроса) остается верным и в более широких предположениях, когда уравнения задаются дифференциальными уравнениями

(11)

Будем считать, что сущствует отличный от 0 якобиан порядка m

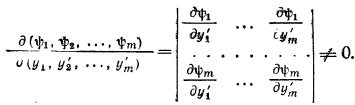
Тогда из системы диф уравнений 11 можно определить функции у1, у2, …у_mчерез независимые функции у_m+1, у_{m+2, …}у_n

Теорема 2. если система функций у1(х), у_n(х), удовлетворяющая уравнениям связи 11 и граничным условиям 2 (из вопроса 18), дает экстремум функционали 1, то существуют такие функцииλ_m(x), что функции у1, у2, …у_nявляются экстремалями функционала

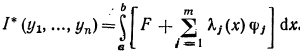(12)

17 47. Уравнение Эйлера - Пуассона.

Поставим задачу — отыскать функцию f(x), для которой первая вариация функционала обращается в нуль:

(59)

Функция f(x) в этом случае называется экстремалью, а значение J(f) — экстремумом функционала.

Равенство (58) 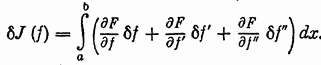не дает сразу ответа для поставленной задачи, так как подынтегральные члены разнородны. Преобразуем правую часть уравнения (58) с помощью интегрирования по частям. Предварительно отметим

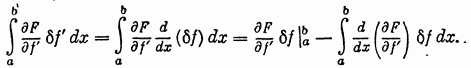(60)

Подобные преобразования дают

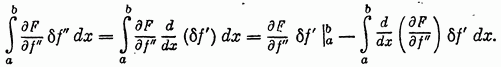(61)

Повторяя интегрирование по частям в последнем члене равенства (61), находим

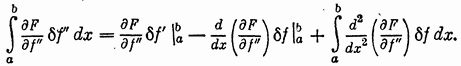
Теперь условие (59) можно записать так:

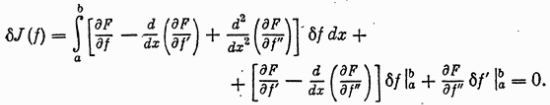
Равенство (63) должно быть справедливым для произвольной вариации δf. В частности, если рассматривать вариации δfи δf‘обращающиеся в нуль на концах интервала, а в промежуточных точках произвольные, то интеграл будет равен нулю только при условии

Это и есть дифференциальное уравнение Эйлера — Пуассона для функции f(x). Опять же в силу произвольности вариации δfдолжны выполняться краевые условия

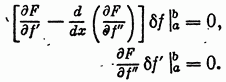
1. Математическая постановка задачи оптимального управления.

1.Задача оптимального управления.Рассмотрим сначала конкретный пример. Пусть имеется двигатель постоянного тока, который работает на механизм М.

Таким механизмом может быть, например, танковая башня. Движением двигателя можно управлять, изменяя напряжение , подводимое к цепи якоря (напряжение будем считать постоянным).

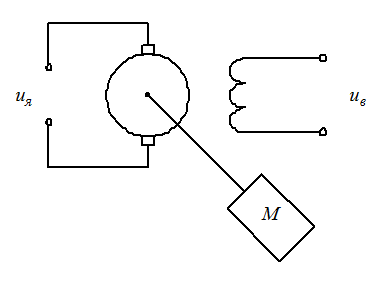
Из условия электрической прочности напряжение, подводимое к цепи якоря, должно быть ограничено:

Пусть требуется осуществить поворот вала двигателя на некоторый заданный угол. Интуитивно ясно, что существует бесконечное множество функцийкоторые решают поставленную задачу, т. е. обеспечивают поворот вала двигателя на заданный угол.

Но тогда естественно поставить ещё одну задачу: среди функций , решающих первую задачу, найти наилучшую в каком - либо смысле, например, осуществляющую поворот на заданный угол за минимально возможное время или с минимальной затратой энергии.

Сформулируем задачу оптимального управления.

Рассмотрим объект или процесс, который описывается системой дифференциальных уравнений

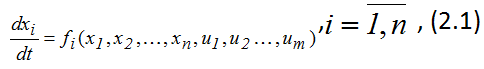
или векторным уравнением

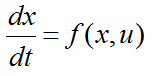
и -n-мерные векторы,-m-мерный вектор управления. Вектор xназывают фазовым вектором системы или вектором состояния.

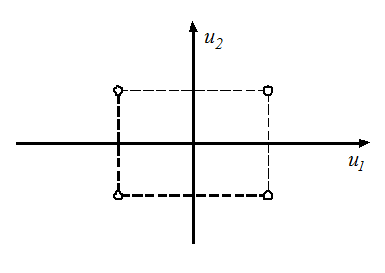
Будем полагать, что вектор управления uможет принимать свои значения из некоторого множестваU.Uможет быть любым множествомm-мерного евклидова пространства, например, оно может состоять из совокупности изолированных точек. На рис. 2.2 приm=2 изображён пример множестваU, состоящего из четырёх изолированных точек.

В этом, кстати, заключается существенное отличие принципа максимума от вариационного исчисления. Из-за принятого способа построения вариаций в вариационном исчислении Uможет быть только областью в классическом смысле этого слова, т. е. когда оно удовлетворяет свойству связности.

Будем предполагать, что в уравнениях (2.1) функции непрерывны по всем своим переменным и непрерывно дифференцируемы по переменным. В качестве допустимых управлений рассматриваются кусочно-непрерывные функции, удовлетворяющие условию.

Векторное пространство с декартовыми координатами будем называть фазовым пространством системы (2.1) и обозначатьX.

Каждому вектору xв фазовом пространстве соответствует некоторая точка (фазовая точка).

Если задан вектор u(t) и начальное условие, то систему уравнений (2.1) можно решить.

Разным вектор-функциям u(t) будут соответствовать различные решенияx(t) уравнений (2.1), т. е. выбором вектораu(t) можно управлять движением системы. Решениюв фазовом пространствеXсоответствует некоторая линия, которая называется фазовой траекторией системы.

Пусть в фазовом пространстве Xзаданы две точкии.

Рассмотрим следующую задачу. Требуется среди допустимых управлений , т. е. кусочно-непрерывных вектор-функций(моменты и не фиксированы), переводящих фазовую точку системы (2.1) из заданного начального положенияв заданное конечное положениепереводящих фазовую точку системы (2.1) из заданного начального положения в заданное конечное положение , найти управление и траекторию, доставляющие минимум функционалу

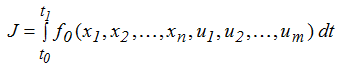(2.2)

Управление u(t) и траекторияx(t), решающие поставленную задачу, называютсяоптимальными.