31 Расчет оптимальных параметров регулятора по уравнениям Риккати.

В инженерной практике часто ставится задача определения оптимальных значений параметров системы, структура и дифференциальные уравнения которой заданы Такая задача обычно решается при расчете параметров оптимальной настройки регуляторов. При этом могут быть использованы уравнения Эйлера-Лагранжа (или Эйлера-Пуассона), уравнения Риккати, а также частотные методы и др

Математически задачу определения параметров оптимальной настройки системы можно сформулировать следующим образом: заданы дифференциальные уравнения состояния системы

(3.186)

матрица, элементы которой зависят от искомых параметров настройки системы (k_ij>0,a_ij,b_ij– коэффициенты уравнения объекта);X,u– векторы координат состояния и управлений;

Требуется определить оптимальные значения параметров системы из условий экстремума выбранного критерия качества.

В ряде практических задач коэффициенты a_ij,b_ijзаданы и требуется определить коэффициентыk_ij.

Если рассматривается критерий качества в виде интеграла с квадратичной подинтегральной функцией, то для определения искомыхk_ij можно использовать уравнения вариационной задачи или Риккати.

Расчет по уравнениям Риккати. Матрицу оптимальных параметров регулятора . с можно определить по заданным уравнениям состояния (3.186) с использованием матричного уравнения Риккати. основываясь на методе принципа максимума Для линейных объектов уравнение (3.114) можно записать в виде (3.186), а минимизируемый квадратичный функционал в общем случае представить в виде

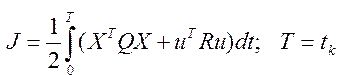(3.194)

Где Q={q_ij}_nxnи R={r_lk}_rxr– матрицы элементы которыхq_ij>0 иr_lk>0

Известно, что вектор координат оптимальных управлений, доставляющих минимум интегралу 3.194 является линейной функцией координат состояния 3.186.

Функция гаамильтона в данном случае при ψ₀ =-1 будет иметь вид

(3.195)

При оптимальном управлении

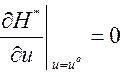или

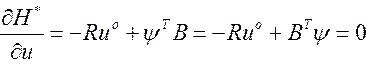
Откуда оптимальное управление

(3.196)

Управление 3.196 обеспечивает максимум Гамильтониана 3.195, так как при положительно определенной матрице R

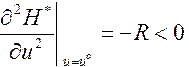
Используя 3.195 и 3.196 запишем канонические уравнения

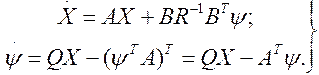(3.197)

Для оптимального управления 3.196 необходимо из уравнений 3.197 найти вектор вспомогательных функций Wс помощью уравнения Риккати:

(3.198)

Дифференцируя которое, найдем

(3.199)

Где K(t) – матрица неизвестных коэффициентов размерностиnxn

Подставив 3.198 в уравнения системы 3.197 получим

(3.200)

Если подставить в 3.199 вместо X’ первое уравнение системы 3.200 то запишем:

(3.202)

Называемое уравнением Риккати. Решение уравнения 3.202 определяет матрицу K(t), подставляя в которую 3.198 и учитывая 3.196 получим выражение для оптимального управления

(3.203)

Для полносью управляемых объектов с постоянными во времени параметрами при tk=T=бесконечности (см.3.194)K’(t)=0 и, поэтому оптмальное управление принимает форму

(3.204)

Откуда

(3.205)

Где - положительно определенная симметричная матрица размерностиnxn, состоящяя из постоянных коэффициентовkij>=0, определяемая уравнение 3.202 с учетом

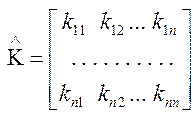(3.206)

Оптимальное управление (3 204) минимизирует квадратичный функционал (3.194) для объектов с постоянными параметрами и tk=T=бесконечности.

Таким образом, для определения оптимальных параметров регулятора необходимо найти матрицу К(с шапочкой) и подставить в (3.205). Для объектов с переменными параметрами, а также с постоянными параметрами при конечной величине tk=Tнеобходимо определять матрицу K(t). Основная трудность решения такой задачи состоит в том. что уравнение (3.202) является нелинейным дифференциальным матричным уравнением, для интегрирования которого требуется применение вычислительных машин. В этом случае регулятор будет иметь переменные параметры, т.е Кос(t)