33. Математическая задача определения параметров оптимальной настройки системы.

35. Оптимальное управление, обеспечивающее оптимальную стабилизацию режима работы объекта.

Оптимальный режим работы объекта характеризуется экстремальным ( максимальным или минимальным) значением показателя эффективности процесса, протекающего в объекте. Таким показателем может быть либо технологическая величина, либо одна из экономических характеристик. Вследствие влияния возмущений оптимальный режим работы объектов нарушается. Системы стабилизации не способны скомпенсировать такие отклонения. Для отыскания оптимального режима служат экстремальные системы. Эта задача решается автоматическим поиском таких значений управляющих воздействий, которые соответствуют экстремальному значению показателя эффективности процесса. Системы, осуществляющие автоматический поиск нескольких управляющих величин объекта с целью обеспечения экстремального значения показателя эффективности протекающего в нем процесса, называются оптимальными. На практике же оптимизируемая величина объекта часто зависит не от нескольких, а от одной управляющей величины; такие оптимальные системы называют экстремальными системами регулирования.

Общий вид уравнений стабилизирующего управления.

В общем случае стабилизирующие управления описываются не алгебраическими уравнениями, а дифференциальными уравнениями вида

где  x_p(t) - n_p-мерный вектор переменных состояния устройства управления (регулятора); иm-мерные векторы соответственно.

В ряде случаев не все переменные состояния объекта управления доступны непосредственному измерению.

Пусть измеряются некоторые переменные , связанные с переменными объекта соотношениями

где  - мерный вектор измеряемых переменных;— заданныйr-мерный вектор. В этом случае уравнения регуляторов имеют вид

Далее будем опускать символ в соотношениях (1.2.2.)...(1.2.9), (1.2.10), относящихся к системам стабилизации. Если теперь для общности изложения заменить функцию под интегралом (1.2.9) функцией, то модели объекта управления и модели целей управления (критерии качества управления) в системах программного управления и стабилизации будут совпадать. Это естественно, так как с математической точки зрения несущественно происхождение этих моделей.

Используя матричную форму, запишем также, отбрасывая символ , уравнения (1.3.2) первого приближения и уравнение (1.2.14) для регулируемых переменных:

где - матрицы, элементами которых являются известные функции времени. Эти матрицы имеют размерысоответственно.

Связь (1.3.6) переменных состояния объекта с измеряемыми переменными часто может быть линеаризована и тогда она с учетом помех измерения принимает вид

где -мерный вектор помех измерения;- заданная матрица размеров.

Устройство управления (регулятор) часто описывается не уравнениями , а линейными уравнениями вида

где матрицы размеровсоответственно.

Часто регулятор содержит управляющую ЭВМ. В этом случае он описывается разностными уравнениями:

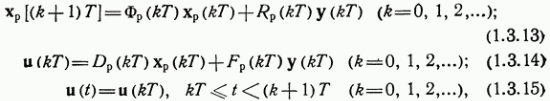
где T — интервал дискретности регулятора; матрицы чисел соответствующих размеров. Поскольку для работы регуляторадостаточно измерения вектора у лишь в дискретные моменты времении т. д., то естественно при определении параметров дискретного регулятора использовать дискретную модель объекта (1.3.9), (1.3.10). Такая модель приимеет вид

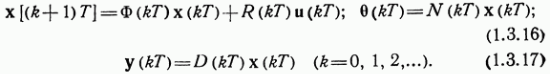
Матрицы нетрудно построить на основе матриц, если воспользоваться формулой Коши

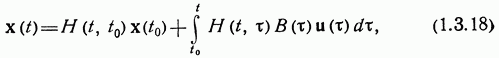
где — нормированная фундаментальная матрица.

Эта матрица (размеров ) составлена изn-мерных векторов (первый вектор — это решение однородного уравнения при начальных условиях )второй вектор является решением однородного уравнения при начальных условиях

Произведение - это импульсная переходная матрица объекта. Ее можно получить экспериментально, прикладываяк входам объекта

Полагая в и принимая во внимание (1.3.15), получим

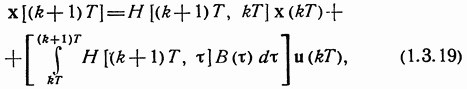
отсюда следует, что

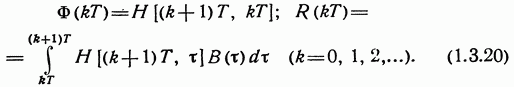
В дискретном случае критерий качества имеет вид

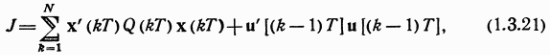
где — заданные положительно-определенные матрицы чисел.

В стационарном случае, когда параметры объекта не изменяются во времени, его уравнения (1.3.9) записываются как

где — заданные матрицы чисел.

Дискретная модель объекта, описываемого уравнениями (1.3.22), имеет () вид

где

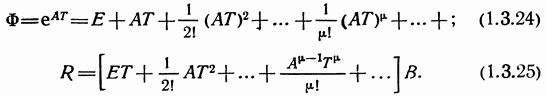
Соотношения нетрудно доказать, если принять во внимание, что в стационарном случае можно указать явный вид нормированной фундаментальной