34. Оптимизация типовых объектов из условия минимума квадратичного функционала.

1. Пример на применение динамического программирования для определения управления, минимизирующего квадратичный функционал.

Пример1. Рассмотрим объект, движение которого задается уравнениями

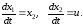
В качестве конечной точки x^*выберем начало координат, т.е. положимx^*=0. Качество процесса управления будем оценивать функционалом

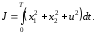(4.27)

Таким образом, речь идет об определении оптимальной стратегии 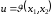, которая обеспечивает перевод фазовой точки из произвольного начального состояния в начало координат и при том так, чтобы на траекториях движения функционал (4.27) принимал наименьшее значение.

Выпишем функциональное уравнение Беллмана

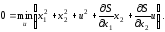(4.28)

Так как на управляющий параметр uне наложено никаких ограничений, то для определения минимума необходимо продифференцировать правую часть уравнения (4.28) поu:

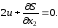(4.29)

Из (4.29) находим

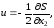(4.30)

и уравнение Беллмана принимает вид

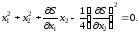(4.31)

Будем искать решение уравнения (4.31) в виде квадратичной формы

Тогда

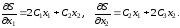
Уравнение (4.31) принимает вид

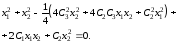
Коэффициенты C₁,C₂,C₃определяются из системы уравнений:

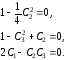(4.32)

Система нелинейных алгебраических уравнений (4.28) имеет два вещественных решения

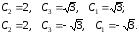
Эти решения в соответствии с (4.30) приводят к двум синтезирующим функциям

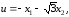(4.33)

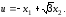(4.34)

В результате получаем две линейные системы, причем линейная система, порождаемая функцией (4.34), оказывается неустойчивой и, следовательно, не может обеспечить перевод фазовой точки в начало координат.

Таким образом, оптимальная синтезирующая функция (оптимальная стратегия) задается равенством (4.33). На рис. 4.1 изображена структурная схема оптимальной системы.

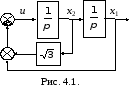
Пример2. Рассмотрим простейшее уравнение

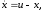(4.35)

полагая, что на управляющий параметр uналожено ограничение

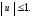
Будем решать задачу перевода переменной xиз произвольного начального значения в нуль.

Как следует из (4.26), уравнение Беллмана имеет вид

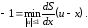(4.36)

Оптимальное по быстродействию управление

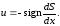(4.37)

Подставляя (4.37) в (4.36), получим уравнение

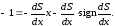(4.38)

Найдем решение уравнения (4.38), полагая . Из соотношения

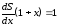
следует, что

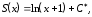(4.39)

здесь C^*- произвольная константа. При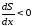аналогичным образом найдем

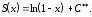(4.40)

Полагая, что равенства (4.38) и (4.40) справедливы при x=0, то в соответствии с граничным условием (4.25)C^*=C^**=0.

Функция 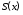задает минимальное время движения и может быть только положительной величиной. Из (4.39) и (4.40) следует тогда, что

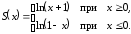(4.41)

Оптимальное по быстродействию управление, таким образом, определяется равенством

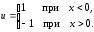
Как следует из (4.41), производная 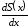имеет разрыв в точкеx=0. Это ставит под сомнение справедливость функционального уравнения Беллмана (4.38). Однако, поскольку в оптимальном движении переменная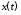не изменяет знак, функцию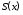можно отдельно рассматривать 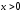прии при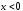, а в каждой из этих областей функция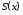является непрерывно дифференцируемой. Это позволяет заключить о справедливости равенства (4.41).

Во избежании недоразумений отметим, что целью настоящего примера является не демонстрация того, как с помощью динамического программирования можно осуществлять синтез оптимального по быстродействию управления, а желание показать, что предположение о непрерывной дифференцируемости функции является весьма существенным ограничением метода динамического программирования, когда он применяется для непрерывных процессов. Этот пример также показывает, что для синтеза оптимального по быстродействию управления целесообразно использовать принцип максимума Понтрягина.