16. Уравнение Эйлера для многих функций и их первых производных.

Различают вариационные задачи с закрепленными и свободными концами. Начнем с рассмотрения задачи в случае закрепленных концов, как наиболее простой. Задача нахождения экстремума для функционала, зависящего от нескольких функций и их первых производных относится к задаче с закрепленными концами.

. Будем считать, что подынтегральные функции в рассматриваемых функционалах непрерывны и обладают непрерывными частными производными до нужного порядка и сами функционалы непрерывны в рассматриваемом пространстве. Изучим простейшую вариационную задачу для функционала и получим для него необходимые условия в виде дифференциального уравнения.

Функционал

Будем рассматривать на множестве функций у(х) ϵС⁽¹⁾,удовлетворяющих граничным условиям

(2)

Это условие означает, что концы допустимых кривых закреплены.

Ставится следующая вариационная задача. Среди всех функций у(х) с граничным условием (2) найти такие, которые дают экстремум функционалу (1). Решение этой задачи будем проводить только в рамках необходимых условий, для чего рассмотрим теорему.

Теорема 1. Если функция у = у (х) ϵС⁽¹⁾удовлетворяет условиям (2) и дает экстремум функционалу (1), то она является решением уравнения Эйлера

(3)

Пусть функция у(х) дает экстремум функционалу 1. По необходимости условию существования экстремума вариация функционала должна равняться 0

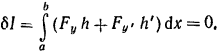(4)

Интегрированием по частям получаем

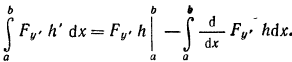
Из граничных условий 2 следует что рассматриваемые приращения h(x) должны обращаться в 0 в точках х=а, х=b

(5)

Подставляя значение интеграла в 4 получаем

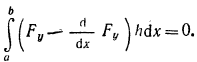
Но функция непрерывна на [a,b], аh(x) – любя функция, непрерывная вместе с первой производной на [a,b] и удовлетворяющая условиям 5. Применяя основную лемму вариационного исчисления, заключаем, что, т.е функция у(х) удовлетворяет уравнению Эйлера (3)

Функции, являющиеся решениями уравнения Эйлера, называют экстремалями.

Теорема 1 дает только необходимое условие существования экстре мума функционала. Но часто само существование экстремума бывает ясно из физических соображений. В этом случае уравнение Эйлера полностью решает вариационную задачу.

Уравнение Эйлера (3) играет фундаментальную роль во всем вари ационном исчислении. Оно представляет собой дифференциальное уравнение второго порядка. Его решение зависит от вух произвольных постоянных. В задаче Коши эти произвольные постоянные находились из начальных условий. Здесь мы имеем другую задачу для Дифференциальных уравнений — краевую задачу, в которой произвольные постоянные находятся из граничных условий.

39. Уравнение Эйлера.

Задачи, решаемые классическим вариационным исчислением, являются частным случаем общей задачи оптимального управления и решаются принципом максимума. Рассмотрим некоторые результаты, которые исторически были получены значительно раньше принципа максимума и нашли широкое применение в различных областях науки и техники. Ограничимся лишь необходимыми условиями оптимальности.

Рассмотрим задачу оптимизации простейшего функционала: среди непрерывных и дифференцируемых функций 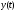, проходящих через заданные точки

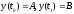, (11.1)

найти функцию 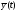, доставляющую минимум функционалу

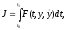(11.2)

где 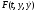- непрерывная и дважды дифференцируемая функция своих аргументов.

Сведем задачу к задаче оптимального управления.

Введем переменную 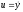, тогда функционал (11.2) примет вид

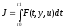(11.3)

при связи

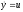(11.4)

и граничных условиях (11.1), что дает задачу оптимального управления. (Заметим только, что в задаче оптимального управления 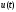допускает разрывы 1-го рода, а мы считаем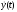непрерывной). Применим принцип максимума:

1. ,

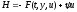2. .

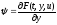3. Из необходимых условий максимума HпоU:

,

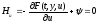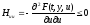. (11.5)

4. Система уравнений

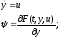(11.6)

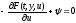(11.7)

сводится к одному уравнению. Из (11.7)

.

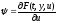Подставляя последнее выражение в (11.5) и используя (11.4), получаем

.

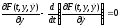Этим доказана следующая теорема.

Теорема (1-е необходимое условие максимума). Элемент минимума функционала

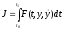
удовлетворяет уравнению

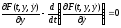, (11.8)

которое называют уравнением Эйлера, а функции, удовлетворяющие ему, -экстремалями. Уравнение (11.8) есть обыкновенное дифференциальное уравнение 2-го порядка, граничные условия, необходимые для однозначного его решения, задаются (11.1).