51. Задача Лагранжа. Синтез оптимальных систем.

Постановки задач. Важным этапом в историй естествознания явилось сочинение Жозефа Луи Лагранжа «Аналитическая механика», опубликованное в 1788 г. В частности, трактат Лагранжа сыграл исключительную роль и в развитии вариационного исчисления. Вариационными задачи на условный экстремум (связанный экстремум) называются задачи, в которых требуется найти кривые, доставляющие экстремум функционалу, при этом помимо граничных условий они должны удовлетворять некоторым связям (условиям). Например, эти кривые должны иметь заданную длину (изопериметрическая задача) либо удовлетворять некоторой заданной системе дифференциальных уравнений (задача Лагранжа), либо лежать на некоторой поверхности.

В 1759 году появилась первая работа Лагранжа по вариационному исчислению. Лагранж развил идею Эйлера для случая, когда экстремали x_i(t) функционала

(4.1)

должны удовлетворять на ряду с граничными условиями еще дополнительным связям в виде дифференциальных уравнений:

(4.2)

Эти уравнения получаются из описания динамики объекта управления.

Задача с дополнительными дифференциальными (или голономными) связями называется общей задачей Лагранжа по определению условного экстремума функционала.

Для решения этой задачи составляется вспомогательная функция:

. (4.3)

Или в сокращенном виде:

, (4.4)

где F– подынтегральная функция критерия (функционала) (4.1) или (3.1),

f_i– дифференциальные уравнения связи (4.2),

- некоторые дополнительные функции (множители Лагранжа), подлежащие определению.

На основе вспомогательной функции составляется вспомогательный функционал:

(4.5)

Этот функционал, зависящий от "n” функций xi(t) и от “n” функций , исследуется на безусловный экстремум, так как благодаря введению функциивсе функции хi могут варьироваться независимо. В результате получаем задачу Эйлера.

Для функционала (4.5) записываем “n” уравнений названных уравнениями Эйлера-Лагранжа:

(4.6)

или подставляя из(4.4) выражение для , получим:

. (4.7)

Эти уравнения совместно с уравнениями (4.2) образуют систему из 2nуравнений с 2nнеизвестными, т.е. задача имеет решение. При этом постоянные интегрирования определяются из граничных условий.

Рассмотрим решение общей задачи Лагранжа для объекта второго порядка:

. (4.8)

Запишем уравнение динамики объекта в фазовых переменных (координатах):

x₁=q_з-y;.

Исходя из (4.8) получаем:

, (4.9)

где а₂₁=.

Граничные условия:

x₁(t_н)=х_1н; х₂(t_к)=х_2н=0 (y=q_з); х₁(t_к)=х_1к=0;x₂(t_к)=х_2к=0.

Задан квадратичный интегральный критерий оптимальности:

(4.10)

Требуется определить оптимальный в смысле критерия (4.10) закон изменения управляющего воздействия u_опт(t), при котором объект из начального состояния х_1н, х_2нпереводится в конечное состояние х_1к, х_2к(оптимальное программное управление) и оптимальный регуляторu_опт(х₁, х₂) для замкнутой САУ.

Принимая во внимание (4.1) и (4.9) запишем выражения для вспомогательного функционала:

. (4.11)

Следующим этапом является получение системы уравнений Эйлера-Лагранжа (4.7)

Для объекта второго порядка (i=1,2) они будут иметь вид:

(4.12)

Определим, что:

Очевидно, что:

.

Аналогично:

Подставляя значения частных производных в уравнения (4.12) получим:

(4.13)

Оптимальное значение управляющего воздействия должно доставлять минимальное значение функционалам JиJ^*. Поэтому должно выполняться условие, что

(4.14)

Подставляя в (4.14) выражение (4.11), получим:

(4.15)

Следовательно

(4.16)

Таким образом, чтобы определить оптимальный закон управления u_опт(t), нужно определить из системы дифференциальных уравнений (4.14) и уравнений динамики объекта (4.9) выражение дляс учетом выражения (4.16) получим:

(4.17)

Характеристическое уравнение системы (4.17):

р⁴ - 2Вр²+с=0, (4.18)

где В=,

Корни уравнения (4.18) будут:

(4.19)

Общим решением уравнения (4.17) будет:

. (4.20)

Из начальных условий следует, что слагаемые в (4.20) с положительными корнями р₁и р₃равны нулю, т.е. с₁=0 и с₃=0. Таким образом:

(4.21)

Аналогично:

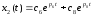(4.22)

Значения постоянных интегрирования с₂, с₄,с₆, с₈– определяются из граничных условий. Подставив (4.22) в (4.16) получим закон изменения управляющего воздействия для оптимального программного регулятора:

, (4.33)

где ;.

Для определения закона оптимального управления для замкнутой САУ необходимо найти зависимость управляющего воздействия от переменных состояний объекта u_опт(x₁,x₂). Для этого выразим производнуючерез переменные состояния объекта. Для этого возьмем первую и вторую производные от х₁(t), определяемую выражением (4.21). В результате получим, что:

(4.24)

Подставив выражение (4.24) во второе уравнение системы (4.17) получим:

u_опт=-к₁х₁-к₂х₂(4.25)

где к₁=р₂р₄+а₂₁; к₂=р₂+р₄+а₂₂ (4.26)

Значения р₂и р₄ определяются выражением (4.19).

Таким образом получаем замкнутую систему с ПД регулятором, коэффициенты которого определяются соотношением (4.26) (см.рис. 4.1)

Рис. 4.1. Замкнутая система управления с оптимальным по критерию (4.10)

с ПД регулятором.

Если представить модель объекта управления в переменных состояния (4.9), то структурная схема САУ будет иметь вид, представленный на рис. 4.2. В этом случае ПД-регулятор превращается в регулятор состояния объекта.

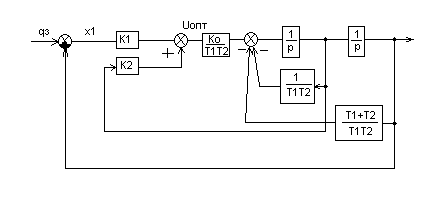
Рис. 4.2 Замкнутая система управления с оптимальным по критерию (4.10)

с регулятором состояния.

Оба регулятора дают один и тот же результат. Схема с регулятором состояния имеет то преимущество, что не надо производить операцию дифференцирования. Но применение этой схемы возможно, если х₂- измеряемое, а иначе надо использовать наблюдатель состояния объекта.