
- •Оглавление
- •57 58 Задача Больца и Майера
- •32 65 67 Уравнение Риккати. Пример
- •31 Расчет оптимальных параметров регулятора по уравнениям Риккати.
- •16. Уравнение Эйлера для многих функций и их первых производных.
- •39. Уравнение Эйлера.
- •14 41 Представление уравнений Эйлера для частных случаев.
- •13. 40 Уравнение Эйлера в развернутом виде.
- •46. Уравнение Эйлера для n – функций и их n первых производных.
- •9. Определение свойств уравнения Эйлера.
- •51. Задача Лагранжа. Синтез оптимальных систем.
- •61. Метод множителей Лагранжа.
- •18. Задача Лагранжа на условный экстремум при конечных связях.
- •49. Система уравнений Эйлера – Лагранжа при конечных связях.
- •19. Задача Лагранжа на условный экстремум при дифференциальных связях.
- •50. Система уравнений Эйлера – Лагранжа при дифференциальных связях.
- •17 47. Уравнение Эйлера - Пуассона.
- •1. Математическая постановка задачи оптимального управления.
- •2. Критерии качества.
- •60. Критерии качества методов оптимизации.
- •4. 69 Квадратичный критерий оптимизации.
- •5. 70 Задача оптимизации систем управления по расходу топлива
- •10. Функции близкие по ординате и производной
- •11. Исследование функционалов с закрепленными и подвижными границами.
- •12. 43 Определение условия трансверсальности.
- •15. 45 Определение теоремы Лежандра.
- •20. Области оптимального управления
- •21. 22 Определите гамильтониан
- •25. Теорема обn-интервалах
- •27. 64 Принцип оптимальности.
- •29. Постановка задачи аналитического конструирования регулятора.
- •30. Задача а. М. Лётова
- •33. Математическая задача определения параметров оптимальной настройки системы.
- •35. Оптимальное управление, обеспечивающее оптимальную стабилизацию режима работы объекта.
- •44. Задача о брахистохроне.
- •57. Задача Майера.
- •24 66. Системы, оптимальные по быстродействию.
- •3 68. Допустимое управление.
- •6.Определение функционала как переменной величины.
- •8. 38 Сравнительный анализ функции и функционалов.
- •1.2 . Различные виды функционалов
- •37. Формы аналитического выражения функционала.
- •7.Определение методов вариационного исчисления по исследованию функционалов на экстремум.
- •10. Функции близкие по ординате и производной
- •23. Теорема Понтрягина
- •63.Принцип максимума Понтрягина.
- •26. Постановка задачи. Постановка задачи оптимального управления.
- •28. Уравнение Беллмана.
- •62.Метод динамического программирования Беллмана.
- •34. Оптимизация типовых объектов из условия минимума квадратичного функционала.
- •36. Задача вариационного исчисления.
- •42. Граничные условия в задачах вариационного исчисления.
- •48. Вариационные задачи на условный экстремум.
- •59. Вариационная задача оптимизации при ограничениях на управление
- •1.2 . Различные виды функционалов
- •1.3 . Задача оптимального управления
- •52. Изопериметрические вариационные задачи.
- •53. Синтез оптимальных систем при изопериметрических связях.
- •54. Изопериметрическая задача. Оптимальная система по экономичности.
- •55. Изопериметрическая задача. Оптимальная система по быстродействию.
- •56. Изопериметрическая задача. Оптимальная система по производительности.
4. 69 Квадратичный критерий оптимизации.
Определение передаточной функции или импульсной характеристики оптимального регулятора при детерминированных воздействиях связано с серьезными трудностями по условиям физической реализуемости. Этих трудности удается избежать, если критерий качества для детерминированных воздействий задать в следующей форме:
при отсутствии ограничений на управляющее воздействие u
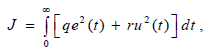
при наличии
ограничений
![]()
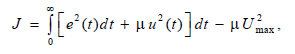
где qиr– весовые коэффициенты,![]() –
множитель Лагранжа, которые находят в
процессе решения задачи.
–
множитель Лагранжа, которые находят в
процессе решения задачи.
5. 70 Задача оптимизации систем управления по расходу топлива
Пусть дана система
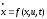 ,
которая может описывать динамику полета
ракеты, а функция управленияuявляется тягой, приложенной к ракете.
Очевидно, чтоuбудет
определяться величиной изменения
расхода топлива, тогда критерий качества
системы можно представить в виде
функционала
,
которая может описывать динамику полета
ракеты, а функция управленияuявляется тягой, приложенной к ракете.
Очевидно, чтоuбудет
определяться величиной изменения
расхода топлива, тогда критерий качества
системы можно представить в виде
функционала
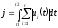 ,
(4.1)
,
(4.1)
характеризующего общий расход топлива.
Задача управления может быть в этом случае сформулирована следующим образом. Необходимо найти u(t), переводящее системы из положенияx1приt1вx2приt2 таким образом, чтобы расход топлива был минимальным.
Пример 3: Пусть
объект описывается уравнением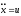 ,
где
,
где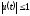 .
Задача регулятора – перевести объект
из произвольной точки х0в начало
координат за времяT,
обеспечив при этом минимум функционала
.
Задача регулятора – перевести объект
из произвольной точки х0в начало
координат за времяT,
обеспечив при этом минимум функционала
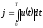 (4.2)
(4.2)
В приведенной
задаче важную роль имеет верхний предел
функционала. Если Т меньше t*,
гдеt* соответствует
минимально возможному времени достижения
начала координат из точки х0, то
решение задачи не существует. Таким
образом необходимо, чтобы выполнялось
условиеT>=t*.
Кроме того время Т должно быть ограничено.
Функционал вида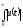 ,
лишен смысла при некоторых начальных
условиях. Далее, если
,
лишен смысла при некоторых начальных
условиях. Далее, если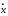 иx– координаты фазовой
плоскости, то даже при
иx– координаты фазовой
плоскости, то даже при изображающая точка из положения х0
в четвертом квадранте будет
перемещаться по горизонтали налево, а
во втором квадранте – направо. Пусть
изображающая точка х0расположена
на положительной оси х. Для ее перемещения
в начало координат необходимо приложить
малое отрицательное управлениеu(t).
Тогда изображающая точка будет двигаться
под осью к началу координат с бесконечно
малой скоростью. Когда она достигнет
точки ниже начала координат, необходимо
создать бесконечно малое приращениеu(t) в
положительном направлении, чтобы
изображающая точка попала в начало
координат. Расход топлива в этом случае,
очевидно, может быть сколь угодно малым.
изображающая точка из положения х0
в четвертом квадранте будет
перемещаться по горизонтали налево, а
во втором квадранте – направо. Пусть
изображающая точка х0расположена
на положительной оси х. Для ее перемещения
в начало координат необходимо приложить
малое отрицательное управлениеu(t).
Тогда изображающая точка будет двигаться
под осью к началу координат с бесконечно
малой скоростью. Когда она достигнет
точки ниже начала координат, необходимо
создать бесконечно малое приращениеu(t) в
положительном направлении, чтобы
изображающая точка попала в начало
координат. Расход топлива в этом случае,
очевидно, может быть сколь угодно малым.
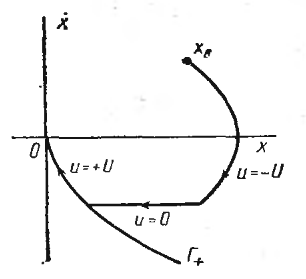
Рисунок 4 – Оптимальная по расходу топлива траектория движения объекта управления
10. Функции близкие по ординате и производной
11. Исследование функционалов с закрепленными и подвижными границами.
12. 43 Определение условия трансверсальности.
1. Задача с
закрепленным временем.Выше была
сформулирована задача оптимального
управления. При этом предполагалось,
что время движения не задано. Поскольку
уравнения (2.1) являются автономными, то
можно положить начальный момент времени фиксированным, а конечный момент времени
фиксированным, а конечный момент времени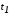 свободным.
свободным.
Будем теперь считать,
что моменты времени
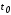 и
и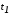 фиксированы. Это приведёт к тому, что
из необходимых условий минимума выпадет
соотношение
фиксированы. Это приведёт к тому, что
из необходимых условий минимума выпадет
соотношение
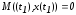 . (2.52)
. (2.52)
Таким образом, необходимые условия оптимальности для задачи с фиксированным временем движения задаются теоремой 2.1, из формулировки которой следует исключить условие (2.52). Отметим, что соотношение
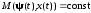
по-прежнему сохраняет свою
силу. Однако функция
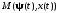 теперь не обязательно должна равняться
нулю.
теперь не обязательно должна равняться
нулю.
2.
Задача с подвижными концами. Выше
предполагалось, что начальное и конечное
состояние системы строго определены,
т.е. в фазовом пространстве заданы
начальная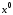 и конечная
и конечная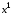 точки, которые следует соединить
оптимальной траекторией. Рассмотрим
более общий случай. Предположим, что
вместо начальной и конечной точек заданы
начальное
точки, которые следует соединить
оптимальной траекторией. Рассмотрим
более общий случай. Предположим, что
вместо начальной и конечной точек заданы
начальное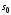 и конечное
и конечное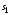 многообразия. Пусть многообразие
многообразия. Пусть многообразие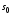 задаётся
уравнениями
задаётся
уравнениями
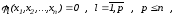 (2.53)
(2.53)
а многообразие
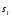 -
уравнениями
-
уравнениями
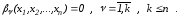 (2.54)
(2.54)
Если n=3, аp=k=1, то многообразия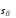 и
и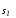 представляют
собой поверхности в трехмерном фазовом
пространстве. Приn=3,p=2, k=1
многообразие
представляют
собой поверхности в трехмерном фазовом
пространстве. Приn=3,p=2, k=1
многообразие задается
как множество, образованное пересечением
двух поверхностей (рис. 2.15), т.е. является
линией в трехмерном фазовом пространстве,
а многообразие
задается
как множество, образованное пересечением
двух поверхностей (рис. 2.15), т.е. является
линией в трехмерном фазовом пространстве,
а многообразие по-прежнему представляет собой
поверхность.
по-прежнему представляет собой
поверхность.
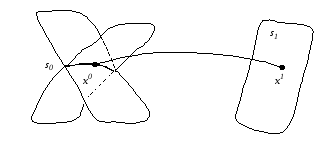
Рис. 2.15.
Функции
 и
и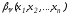 ,
,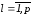 ,
,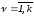 ,
будем полагать непрерывно дифференцируемыми
по всем своим аргументам. Введем вектор
,
будем полагать непрерывно дифференцируемыми
по всем своим аргументам. Введем вектор
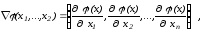
называемый
градиентом функции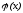 .
.
Многообразие
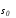 называетсягладким, если в каждой
точке
называетсягладким, если в каждой
точке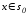 следующие векторы
следующие векторы
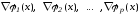 (2.55)
(2.55)
линейно независимы. Условие линейной независимости векторов (2.55) эквивалентно требованию, чтобы ранг матрицы
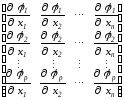
был равен p.
Аналогичным образом определяется
гладкость многообразия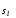 .
В дальнейшем многообразия
.
В дальнейшем многообразия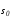 и
и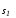 полагаются
гладкими.
полагаются
гладкими.
Рассмотрим следующую
задачу: требуется среди допустимых
управлений u(t), переводящих
фазовую точкуxс многообразия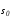 на
многообразие
на
многообразие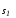 ,
найти такое, которое доставляет минимум
функционалу (2.2). Так как в поставленной
задаче концы траекторииx(t) могут
скользить по многообразиям
,
найти такое, которое доставляет минимум
функционалу (2.2). Так как в поставленной
задаче концы траекторииx(t) могут
скользить по многообразиям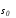 и
и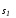 ,соответствующую
задачу оптимального управления будем
называтьзадачей с подвижными концами.
,соответствующую
задачу оптимального управления будем
называтьзадачей с подвижными концами.
Пусть u(t) иx(t),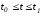 ,
- управление и траектория, решающие
поставленную выше задачу оптимального
управления с подвижными концами. Но
тогда найдутся точки
,
- управление и траектория, решающие
поставленную выше задачу оптимального
управления с подвижными концами. Но
тогда найдутся точки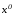 и
и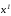 ,
лежащие соответственно на многообразиях
,
лежащие соответственно на многообразиях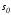 и
и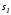 (рис. 2.15). Ясно, что управлениеu(t) и
траекторияx(t)являются оптимальными
и в смысле рассмотренной в п.2.1 двухточечной
задачи оптимального управления, т. е.
управлениеu(t) и траекторияx(t)должны удовлетворять принципу максимума
(теореме 2.1).
(рис. 2.15). Ясно, что управлениеu(t) и
траекторияx(t)являются оптимальными
и в смысле рассмотренной в п.2.1 двухточечной
задачи оптимального управления, т. е.
управлениеu(t) и траекторияx(t)должны удовлетворять принципу максимума
(теореме 2.1).
Таким образом
принцип максимума (теоремы 2.1 и 2.2)
остается в силе и для задачи с подвижными
концами. Однако в этом случае необходимо
иметь некоторые дополнительные условия,
которые позволили бы определить положение
точек
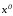 и
и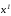 на многообразиях
на многообразиях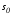 и
и .
.
Для получения указанных дополнительных условий обратимся к п.1.5, в котором приводятся необходимые условия оптимальности, полученные методами классического вариационного исчисления. Дополнительные условия задаются соотношениями (1.79). Выпишем эти условия, используя обозначения, принятые в принципе максимума:
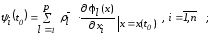 (2.56)
(2.56)
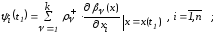 (2.57)
(2.57)
здесь
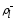 и
и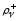 ,
,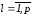 ,
,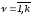 ,
- некоторые числа. Во избежание
недоразумений отметим, что имеющееся
в (1.79) дополнительное условие вида
,
- некоторые числа. Во избежание
недоразумений отметим, что имеющееся
в (1.79) дополнительное условие вида
 (2.58)
(2.58)
в равенстве (2.56)
опущено, так как
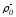 − произвольное число, и, следовательно,
соотношение (2.58) не несет какой-либо
новой информации.
− произвольное число, и, следовательно,
соотношение (2.58) не несет какой-либо
новой информации.
Будем говорить,
что на левом конце траектории x(t) (в
момент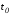 )
выполнено условие трансверсальности,
если найдутся такие числа
)
выполнено условие трансверсальности,
если найдутся такие числа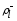 (
(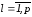 ),
что имеют место соотношения (2.56).
Аналогично, говорят, что на правом конце
траекторииx(t) выполнены условия
трансверсальности, если найдутся такие
числа
),
что имеют место соотношения (2.56).
Аналогично, говорят, что на правом конце
траекторииx(t) выполнены условия
трансверсальности, если найдутся такие
числа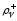 (
(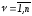 ),
при которых выполняются равенства
(2.57). В смешанном случае, т. е. когда один
конец траектории закреплен, а второй
подвижен, условия трансверсальности
следует относить к подвижному концу
траектории.
),
при которых выполняются равенства
(2.57). В смешанном случае, т. е. когда один
конец траектории закреплен, а второй
подвижен, условия трансверсальности
следует относить к подвижному концу
траектории.
Сформулируем окончательный результат. Необходимые условия оптимальности в задаче с подвижными концами заключаются в следующем:
оптимальное управление u(t) и траектория x(t) должны удовлетворять принципу максимума (теореме 2.1 или 2.2);
на подвижных концах траетории должны выполняться условия трансверсальности.
Условия
трансверсальности являются теми
дополнительными условиями, которые
позволяют, в конечном счете, определить
начальную и конечную точки, лежащие на
многообразиях
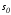 и
и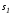 .
Действительно, координаты неизвестных
точек
.
Действительно, координаты неизвестных
точек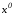 и
и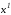 вместе с
вместе с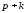 неопределенными множителями Лагранжа
неопределенными множителями Лагранжа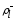 ,
,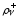 ,
,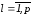 ,
,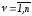 ,
приводят к
,
приводят к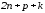 неизвестным числам. Для определения
указанных чисел необходимо воспользоваться
неизвестным числам. Для определения
указанных чисел необходимо воспользоваться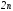 условиями трансверсальности (2.56), (2.57)
и
условиями трансверсальности (2.56), (2.57)
и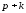 уравнениями (2.53), (2.54), т. е. число неизвестных
совпадает с числом уравнений.
уравнениями (2.53), (2.54), т. е. число неизвестных
совпадает с числом уравнений.
Формально условиями
трансверсальности можно пользоваться
и в том случае, когда в уравнениях (2.53)
и (2.54) p=k=n.Уравнения (2.53) и (2.54) в этом случае задают
соответственно начальную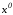 и конечную
и конечную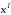 точки, т. е. имеет место двухточечная
задача оптимального управления.
Использовать условия трансверсальности
в двухточечной задаче оптимального
управления вряд ли целесообразно, так
как это может только усложнить решение
задачи.
точки, т. е. имеет место двухточечная
задача оптимального управления.
Использовать условия трансверсальности
в двухточечной задаче оптимального
управления вряд ли целесообразно, так
как это может только усложнить решение
задачи.
Выясним геометрический смысл соотношений (2.56) и (2.57). Для этого запишем их в векторной форме:
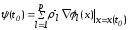 ;
(2.59)
;
(2.59)
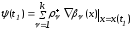 ;
(2.60)
Известно, что
вектор
;
(2.60)
Известно, что
вектор
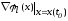 (2.61)
ортогонален
к поверхности
(2.61)
ортогонален
к поверхности
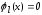 (2.62)
(2.62)
в точке
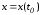 .
Многообразие
.
Многообразие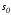 образовано пересечением
образовано пересечением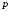 поверхностей (2.53). Поэтому вектор (2.61),
являясь ортогональным к поверхности
(2.62), ортогонален и к многообразию
поверхностей (2.53). Поэтому вектор (2.61),
являясь ортогональным к поверхности
(2.62), ортогонален и к многообразию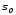 ,
которое принадлежит поверхности (2.62).
Таким образом, правая часть равенства
(2.59) является линейной комбинацией
векторов, каждый из которых ортогонален
многообразию
,
которое принадлежит поверхности (2.62).
Таким образом, правая часть равенства
(2.59) является линейной комбинацией
векторов, каждый из которых ортогонален
многообразию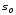 .
Поскольку векторы (2.55) линейно независимы,
то вектор (2.59) является ортогональным
к многообразию
.
Поскольку векторы (2.55) линейно независимы,
то вектор (2.59) является ортогональным
к многообразию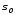 в точке
в точке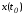 вектором общего положения. Аналогичным
образом, можно показать, что вектор,
стоящий в правой части равенства (2.60),
является ортогональным к многообразию
вектором общего положения. Аналогичным
образом, можно показать, что вектор,
стоящий в правой части равенства (2.60),
является ортогональным к многообразию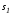 в точке
в точке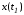 вектором общего положения.
вектором общего положения.
Вектор Yназывается ортогональным к многообразию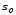 в точке
в точке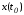 ,
если он ортогонален к плоскости, которая
касается многообразия
,
если он ортогонален к плоскости, которая
касается многообразия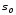 в точке
в точке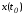 .
Касательная к многообразию
.
Касательная к многообразию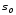 плоскость образуется пересечениемpплоскостей, каждая из которых касается
в точке
плоскость образуется пересечениемpплоскостей, каждая из которых касается
в точке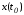 одной из поверхностей
одной из поверхностей
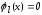 ,
,
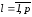 .
.
Обозначим
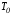 плоскость касательную к многообразию
плоскость касательную к многообразию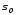 ,
а
,
а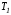 - плоскость касательную к многообразию
- плоскость касательную к многообразию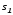 .
.
Условия
трансверсальностиможно сформулировать
в следующем виде. Говорят, что на правом
конце траекторииx(t) выполнено
условие трансверсальности, если вектор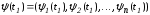 ортогонален плоскости
ортогонален плоскости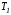 .
Аналогичным образом формулируется
условие трансверсальности и для левого
конца траекторииx(t).
.
Аналогичным образом формулируется
условие трансверсальности и для левого
конца траекторииx(t).
