14 41 Представление уравнений Эйлера для частных случаев.

При некоторых частных случаях задания функции 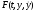можно сразу указать первые интегралы уравнения Эйлера.

,

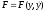первый интеграл .

,

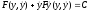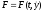первый интеграл .

,

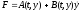уравнение Эйлера

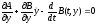
есть уравнение 1-го порядка, так что его решение не может удовлетворить любым граничным условиям (11.1) – тогда решение исходной задачи в общем случае не существует.

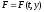- частный случай предыдущего.

13. 40 Уравнение Эйлера в развернутом виде.

Представим уравнение Эйлера в следующем развернутом виде:

(1)

       Переменная, которая не содержится явным образом в выражении для функции  F, называется циклической.

46. Уравнение Эйлера для n – функций и их n первых производных.

Вариационная задача для функционала, зависящего от nфункций – необходимо найти условия экстремума для функционала

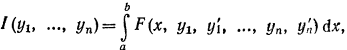(10)

Зависящего от nфункций у1, у2,…у_nϵС⁽¹⁾, удовлетворяющих граничным условиям

(11)

Ответ дается в виде теоремы: Если система линейно независимых функций у1(х), у2(х),..у_n(х), удовлетворяющих условиям 11, дает экстремум функционалу 10, то она является решением системы дифференциальных уравнений Эйлера

(12)

Вариация функционала 10 записывается в виде

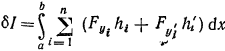
Все приращения hi(x) независимы, поэтому одно из них, напримерh_v, выбираем произвольно с соблюдением граничных условий, а все остальные будем считать равными нулю, т.е.

Из необходимого условия экстремума функционала можем записать, что

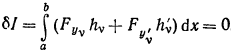(13)

Имеем простейшую вариационную задачу, к ней можно применить теорему, согласно которой у_v(х) должна удовлетворять уравнению. Но равенство 12 можно записать для любогоv=1,2,…n, следовательно, одновременно каждая из функций у1(х), у2(х),..у_n(х) удовлетворяют решению эйлера, т.е их совокупность является решением системы уравнений Эйлера. Система состоит изnуравнений 2 порядка. ЕЕ общее решение содержит 2nпроизвольных постоянных, которые находятся из граничных условий 10.

Функционалы. Зависящие от производных высших порядков. Рассмотрим вариационную задачу для функционала

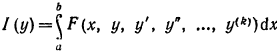(14)

Заданного на множестве функций, принадлежащих пространству С^к и удовлеторяющих граничным условиям

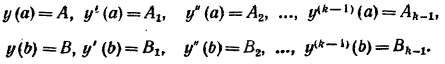(15)

Получим необходимое условие существования экстремума функционала 14 в случае закрепленных концов 15.

Теорема 3. Если функция у(х)ϵС^к , удовлетворяющая граничным условиям 15, дает экстремум функционалу 14, то она является решением дифференциального уравнения Эйлера-Пуассона

(16_

Вариация функционала записывается в виде

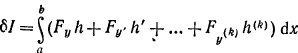
Интегрируя по частям, имеем

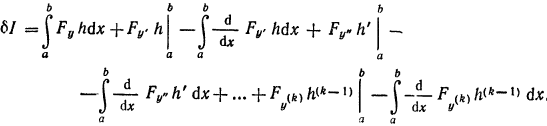
Из граничных условий 15 следует что рассмариваемые приращения h(x) удовлетворяют условиям

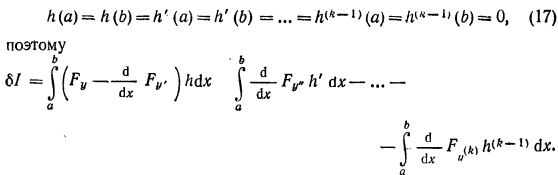
Интегрируя необходимое число раз второй и последующие интегралы по частям и используя условия 17, получаем

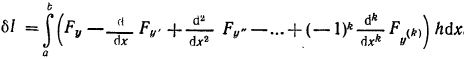
Применяя необходимое условие существования экстремума функционала, заключаем что δI=0. Из замечания к основной лемме вариационного исчисления следует , что функция, дающая экстремум функционалу 14, должна удовлетворять уравнению Эйлера-пуассона 16, имеющего порядок 2к. Общее решение зависит от 2к произвольных постоянных, которые могут быть определены из граничных условий 15.

9. Определение свойств уравнения Эйлера.

Теорема 1. Для того чтобы функционал

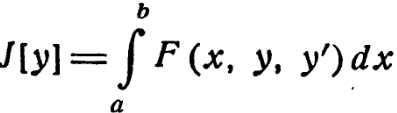
определенный на множестве функций у = у(х), непрерывную первую производную и удовлетворяющих условиям у(а) = А, у(в) — В достигал на данной функции у(х) экстре-

мума*), необходимо, чтобы эта функция удовлетворяла уравнению Эйлера

Интегральные кривые уравнения Эйлера называются экстремалями.

Уравнение Эйлера представляет собой дифференциальное уравнение второго порядка. Его решение должно зависеть, вообще говоря, от двух произвольных постоянных, которые определяются из двух краевых условий у (а) = А и у(Ь) = В.

Отметим, что при решении уравнения Эйлера мы, в отличие от обычной для дифференциальных уравнений постановки вопроса, где ищется решение, определенное в окрестности некоторой точки и удовлетворяющее заданным начальным условиям (задачи Коши), ищем решение, определенное во всей фиксированной области и удовлетворяющее заданным граничным условиям. Поэтому вопрос о разрешимости той или иной вариационной задачи не сводится непосредственно к обычным теоремам существования для дифференциальных уравнений.