36. Задача вариационного исчисления.

Необходимое условие экстремума функционала

Понятие функционала является естественным развитием понятия функции. Говорят, что в классе функций задан функционал, если указано правило, по которому каждой функции из этого класса ставится в соответствие некоторое число.

Например, интеграл

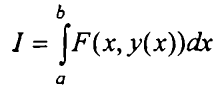
каждой непрерывной функции у(х) ставит в соответствие число, т.е. является функционалом.

Вариационным исчислениемназывается раздел математики, в котором рассматриваются задачи определения максимума и минимума функционалов, а также определения функций (кривых), на которых эти максимумы и минимумы достигаются. Приведем простой примервариационной задачи. На плоскости заданы две точки с координатами (а, В) и (b, В). Требуется среди линий у = у(х) (а<х<b), соединяющих эти точки, найти такую, которая имеет наименьшую длину, т.е. найти функцию у(х), на которой функционал

достигает минимума.

42. Граничные условия в задачах вариационного исчисления.

Вариационная задача с закрепленными граничными точками.

Первое необходимое условие экстремума (уравнение Эйлера).

Исследуем на экстремум (максимум или минимум) функционал

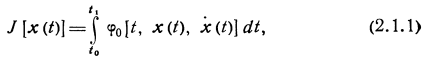
где —непрерывная и трижды дифференцируемая функция своих аргументов.

Искомая функция (для которой этот функционал принимает экстремальное значение) удовлетворяет краевым условиям

Задача о нахождении экстремума функционала (2.1.1) при условиях (2.1.2), в которых x0 иx1 — заданные числа, называетсявариационной задачей с закрепленными граничными точками. Непрерывно дифференцируемые функцииx(t), определенные на [tо,t1] и удовлетворяющие условиям (2.1.2), называютсядопустимыми функциями.

Переходя к решению вариационной задачи, допустим, что ее решение — кривая x°(t)—найдено. Возьмем некоторую функцию(t) и включим ее в однопараметрическое семейство кривых

где а — некоторое число.

Концы варьируемых кривых естественно также закреплять в точках (2.1.2) (рис. 2.1.4), и поэтому

Рассмотрим значения, которые принимает функционал (2.1.1) на кривых семейства (2.1.3),

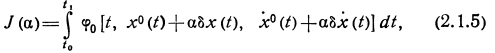
Где

Нетрудно видеть, что при известных кривых x°(t) иx(t) функционал (2.1.1) становится функцией а. Эта функция достигает своего экстремума при а=0, так как, по определению,x(t, 0) =x⁰(t)

Необходимым условием экстремума функции J(а) при а=0 является, как известно, равенство

Подставляя в это условие выражение (2.1.5), получим

После интегрирования по частям

и тогда запишем (2.1.6) окончательно с учетом краевых условий

δx(to)==δx(t1)=0 в виде

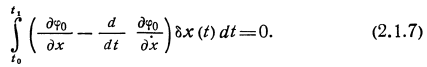
В этом выражении сомножитель является на кривой х⁰(t), реализующей экстремум, заданной непрерывной функцией, а второй сомножитель δx(t)—произвольная (в силу произвола при выборе функции(t)) дифференцируемая функция.

При этих условиях из (2.1.7) следует тождество

которое выполняется на экстремалях x°(t).

Доказательство того, что (2.1.8) следует из (2.1.7), опирается на основную лемму вариационного исчисления, которая формулируется так: если для каждой непрерывной функции η(t) (удовлетворяющей условиюη(to)=η(tl)=0)

где μ(t)—непрерывная на отрезке [t0,t1] функция, то μ(t)=0 на том же отрезке.

Для доказательства леммы предположим (в противоречии с ее утверждением), что в точке tЄ [t0,t1] значение μ(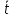)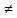0. Тогда придем к противоречию с утверждением леммы. Действительно, из непрерывности функции μ(t) следует, что если μ()0, то μ(t) сохраняет знак в некоторой окрестноститочки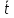. Выбирая функцию η(t) сохраняющей знак на отрезкеЄ[t0,t1] и равной нулю вне этого отрезка, заключаем, что произведение μ(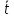) η(t) сохраняет знак на отрезкеи равно нулю вне этого отрезка и, следовательно,

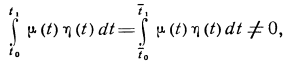
а это противоречие и доказывает лемму. Таким образом, x°(t) является решением уравнения

которое называется уравнением Эйлера.

Принимая во внимание, что

запишем (2.1.10) в развернутой форме:

Его решения x(t, c_lc₂), где с₁и с₂— постоянные, определяемые краевыми условиями (2.1.2), называются экстремалями.