57 58 Задача Больца и Майера

Анализ вариационных задач в зависимости от типа уравнений связи (см. 4.1, 4.2) показывает, что задача Лагранжа является наиболее общей. Другие задачи либо представляют собой частные случаи задачи Лагранжа, либо сводятся к ней.

Проведем классификацию вариационных задач по типу целевого функционала. Задача (4.1)-(4.3) с интегральным целевым функционалом

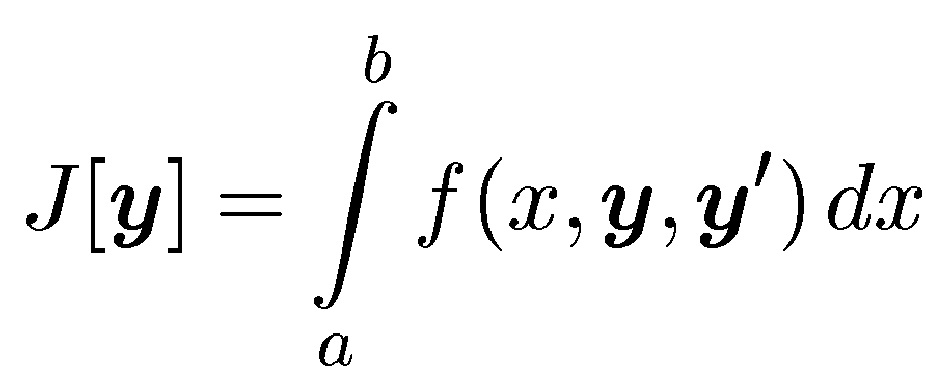
представляет собой, как уже говорилось, задачу Лагранжа. Если в задаче Лагранжа интегральный целевой функционал заменить терминальным целевым функционалом

Т[у]=Т(у(а),у(b)),

который определяется дважды непрерывно дифференцируемой функцией Т(у1,у2) то получим задачу Майера.Задачу сосмешанным целевым функционалом называют задачей Больца. Во всех трех типах задач предполагается, что условия связи имеют вид (4.3), а краевые условия в самом общем виде записываются следующим образом:

где количество s уравнений связано с размерностью nфазового пространства неравенством s <=2n+ 2.

Иногда задачу со смешанным целевым функционалом без ограничений (т.е. без условий связи) называют элементарной задачей Больца.

Задача Больца, так же как и задача Майера, может быть сведена к задаче Лагранжа. Покажем это на примере задачи Больца для целевого функционала вида

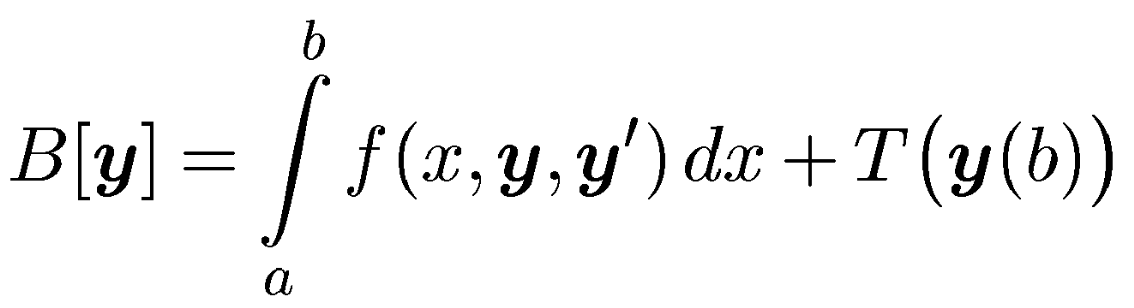(4.29)

С дифференциальными связями (4.3) и краевыми условиями

у(а)=у¹(4.30)

Отрезок [a, b] считаем фиксированным, а функцию Т(у) дважды непрерывно дифференцируемой.

Для рассматриваемой задачи

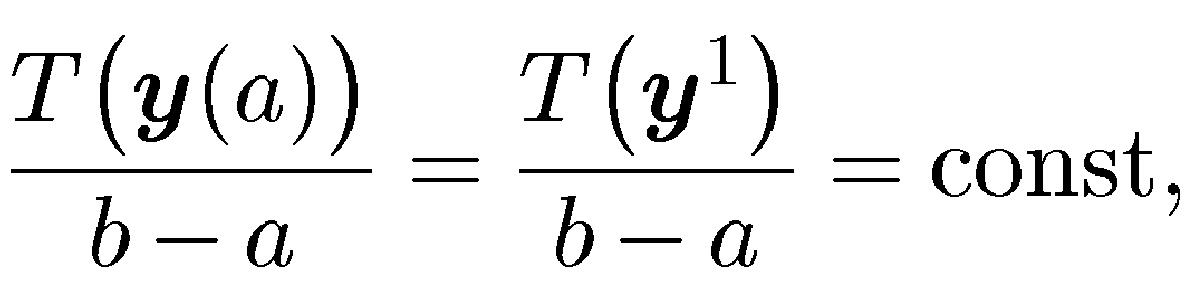
так как а, b, у¹в данной задаче фиксированы. Учитывал это, терминальное слагаемое Т(у(b)) в правой части (4.29) можно преобразовать к виду

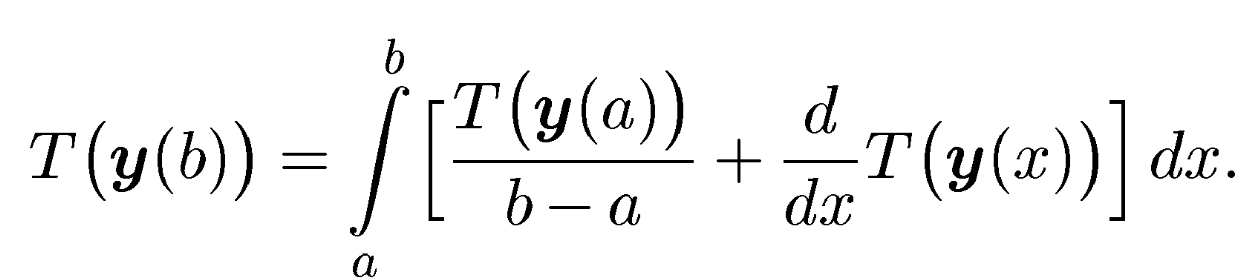
Это позволяет переписать целевой функционал (4.29) в интегральной форме:

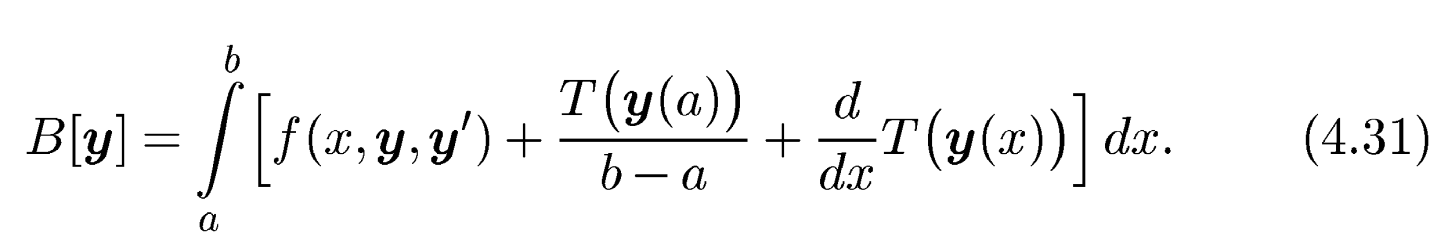
Видим, что задача Больца (4.29), (4.3), (4.30) эквивалентна задаче Лагранжа для функционала (4.31) с теми же условиями связи и краевыми условиями. Опираясь на эту эквивалентность, докажем следующее утверждение.

32 65 67 Уравнение Риккати. Пример

Уравнение Риккати является одним из наиболее интересных нелинейных дифференциальных уравнений первого порядка. Оно записывается в форме:

где a(x), b(x), c(x) − непрерывные функции, зависящие от переменной x.  Приведенное выше уравнение называется общим уравнением Риккати. Его решение основано на следующей теореме: 

Теорема: Если известно частное решение y₁ уравнения Риккати, то его общее решение определяется формулой

Действительно, подставляя решение  y = y₁ + u в уравнение Риккати, имеем:

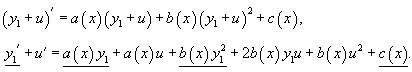
Подчеркнутые члены в левой и правой части можно сократить, поскольку y₁ − частное решение, удовлетворяющее уравнению. В результате мы получаем дифференциальное уравнение для функции u(x):

которое является уравнением Бернулли. Подстановка  z = 1/u преобразует данное уравнение Бернулли в линейное дифференциальное уравнение, допускающее интегрирование.  Помимо общего уравнения Риккати, существует множество частных случаев уравнения Риккати с коэффициентами a(x), b(x), c(x) определенного вида. Многие из этих частных случаев имеют интегрируемые решения. 

Возвращаясь вновь к общему уравнению Риккати, мы видим, что общее решение можно сконструировать, если известно какое-либо частное решение. К сожалению, не существует строгого алгоритма для нахождения частного решения, которое существенно зависит от вида функций a(x), b(x) и c(x). 

Пример. Решить дифференциальное уравнение  y' = y + y² + 1.

Решение.

Данное уравнение является простейшим уравнением Риккати с постоянными коэффициентами переменные x, y здесь легко разделяются, так что общее решение уравнения определяется в следующем виде: