1.3 . Задача оптимального управления

Прогресс в нахождении аналитических методов неклассических вариационных задач возник после постановки общей задачи оптимального управления. Эта задача имеет следующий математический и векторный вид:

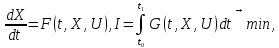
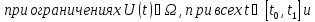
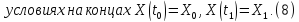
В задаче (8) 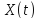представляет собой вектор-функцию времени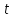и имеет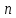координат:

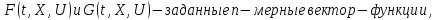
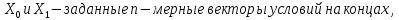
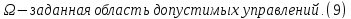
Обычно область 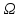задается системой в виде уравнений и нестрогих неравенств, в которых неизвестными являются координаты функции управления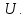

Задача оптимального управления отличается от вариационной задачи Лагранжа, прежде всего, наличием области 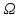и описывающих ее ограничений типа неравенство. Простейшим примером таких ограничений может служить ограничение вида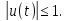

52. Изопериметрические вариационные задачи.

Изопериметрическая задача

Интересный класс задач на условный экстремум образуют так называемые изопериметрические задачи.Классической задачей такого вида (давшей название всему классу задач) является задача Дидоны: найти замкнутую кривую, ограничивающую наибольшую площадь при заданном периметре. При этом и минимизируемый функционал (площадь) и ограничение (периметр) задаются определенными интегралами.

Рассмотрим задачу в общей постановке. Пусть на кривых 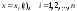с фиксированными концами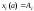,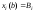функционал

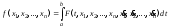
достигает своего минимального (максимального) значения, причем интегралы

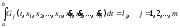
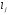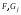обладают заранее заданными значениями . Функциии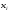считаются дважды непрерывно дифференцируемыми.

На первый взгляд кажется, что интегральные ограничения существенно усложняют задачу, и к изопериметрической задаче неприменимы методы предыдущего раздела. Однако оказалось, что изопериметрическую задачу остроумным приемом можно свести к задаче на условный экстремум с функциональными условиями связи.

Обозначим

.

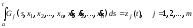Тогда

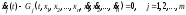
– новые условия связи, уже дифференциально-функционального вида, а изопериметрические условия превращаются в граничные условия:

.

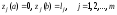Таким образом, задача свелась к задаче на условный экстремум, для которой выше был приведен алгоритм решения. Следуя ему, составляем вспомогательную функцию

,

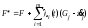для которой система уравнений Эйлера имеет вид:

.

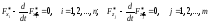Но так как 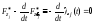, то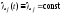, а тогда

.

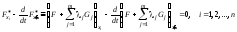Следовательно, для изопериметрической задачи в качестве функции Лагранжа можно взять функцию

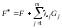
с постоянными множителями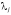. Далее для функции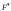, как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров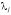используются граничные и изопериметрические условия. То обстоятельство, что множители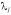оказываются постоянными, безусловно, упрощает решение задачи.

53. Синтез оптимальных систем при изопериметрических связях.

54. Изопериметрическая задача. Оптимальная система по экономичности.

55. Изопериметрическая задача. Оптимальная система по быстродействию.

Пример 10.3. Дано:

уравнения объекта

изопериметрическое ограничение краевые условияx1(0) =x2(0)=0; x1(t_j) = d;x2(t_j)= 0.

Требуется определить оптимальное по быстродействию управление:

J = tj→ min.

Преобразуем изопериметрическое ограничение:

Функция G= —tjи условия трансверсальности записываются следующим образом

Гамильтониан и уравнения Эйлера—Лагранжа имеют следующий вид:

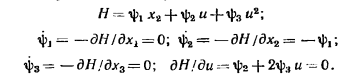
Из последних уравнений имеем:

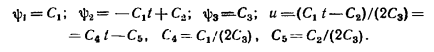
Подставив полученное выражение для управления в исходные уравнения и решив их с учетом краевых условий, получим

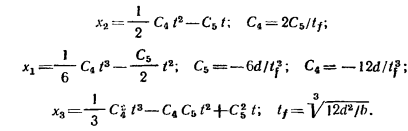
Следовательно, правилу множителей Лагранжа удовлетворяет

Управление

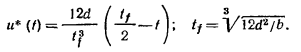
Здесь, предполагается, что решение задачи существует, поэтому единственное управление, удовлетворяющее правилу множителей Лагранжа, будет оптимальным. В данном примере условия трансверсальности при определении оптимального управления не использовались. Они потребовались бы, если нужно было бы определить множители Лагранжа.