48. Вариационные задачи на условный экстремум.

Вариационные задачи на условный экстремум

Вариационными задачами на условный экстремум называются задачи, в которых экстремум функционала находится в предположении, что на функции, от которых зависит функционал, накладываются некоторые дополнительные условия (связи).

Например, пусть ищется экстремум функционала

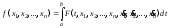(12)

при наличии условий

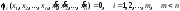. (13)

Наиболее естественный путь заключается в разрешении системы (13), уравнения которой считаем независимыми, относительно каких-нибудь переменных – например, относительно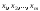– и подстановки найденных переменных в (12). При этом функционал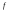будет зависеть уже от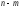переменных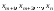,которые уже независимы, и следовательно, задача свелась к исследованию функционала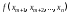на безусловный экстремум. К этой задаче применимы методы, изложенные в предыдущих разделах.

Легко, однако, заметить, что этот метод срабатывает далеко не всегда, поскольку задача явно выразить переменные 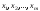через остальные может оказаться очень трудной (если вообще разрешимой). Поэтому для решения вариационных задач на условный экстремум чаще применяют метод, известный какметод множителей Лагранжа.

Этот метод состоит в построении вспомогательной функции

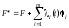, (14)

в терминах которой и формулируется решение задачи на условный экстремум.

Теорема. Пусть функции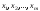реализуют экстремум функционала (12) при условиях связи (13). Тогда функцииявляются решением системы уравнений вида:

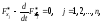
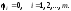(15)

Таким образом, для решения задачи на условный экстремум следует:

1. Составить вспомогательную функцию по формуле (14).

2. Записать и решить для нее систему уравнений Эйлера, дополненную условиями связи (15).

3. Найти произвольные постоянные из граничных условий (они могут быть любого вида, как жестко закрепленные, так и подвижные).

В процессе реализации этой программы, как правило, находятся еще и вспомогательные функции 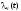, которыене обязательны для построения решения, но могут оказаться полезными при решении системы (15).

59. Вариационная задача оптимизации при ограничениях на управление

Задачи оптимизации при ограничениях в виде нестрогих неравенств. Задача оптимального управления

В рамках классического вариационного исчисления рассматривались задачи на оптимизацию функционалов при ограничениях типа равенство. Однако во многих технических и экономических задачах существуют ограничения вида нестрогих неравенств. Это случается, когда управление ограничено некоторой величиной (например, сила тяги поезда не может превышать некоторое значение). Другим распространенным примером служит ограничение на объем денежных инвестиций в экономический проект. Для решения задач с такими ограничениями нужен новый аппарат. Простой вариант такого аппарата представляет собой непрерывный вариант Динамического программирования, предложенный Р.Беллманом в [4.13]. Другое обобщение классического вариационного исчисления – принцип максимума Л.С. Понтрягина была разработано в [4.12]. Дискретные проблемы оптимального управления подробно рассматриваются в [5.1].

1.2 . Различные виды функционалов

Исторически возникла ситуация, что в классическом вариационном исчислении рассматривались только интегральные функционалы видов

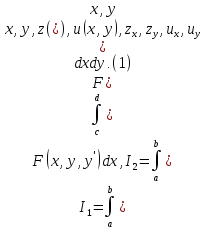
Однако помимо интегральных функционалов в практических задачах возникают и так называемые терминальные функционалы. Простым примером терминального функционала служит значение функции в некоторой точке:

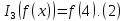
Вариационная задача, в которой требуется оптимизировать интегральный функционал при ограничениях, называется задачей Лагранжа. Вариационная задача, в которой требуется оптимизировать терминальный функционал при некоторых ограничениях, называется задачей Больца. Вариационная задача, в которой требуется оптимизировать сумму интегрального и терминального функционалов при некоторых ограничениях, называется задачей Майера. Несложно показать, что задачи Больца и Майера сводятся к задаче Лагранжа и задача Лагранжа сводится, как к задаче Больца, так и к задаче Майера. Рассмотрим примеры такого взаимного сведения задач.

Пример 1. Пусть требуется свести задачу Лагранжа

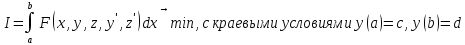
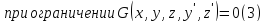
к какой-нибудь задаче Больца.

Решение

Обозначим

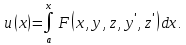
Тогда задача (3) превращается в следующую задачу с терминальным функционалом:

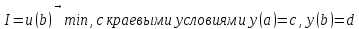
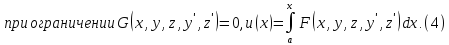
Пример 2. Пусть требуется свести задачу Больца

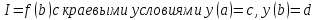
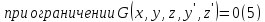
к какой-нибудь задаче Лагранжа.

Решение

Обозначим

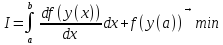
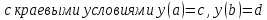
Тогда задача (4) превращается в следующую задачу с интегральным функционалом: