61. Метод множителей Лагранжа.

Правило множителей Лагранжа. Если допустимая пара u(t),x(t)) является решением задачи оптимального управления (10.28)—(10.31)

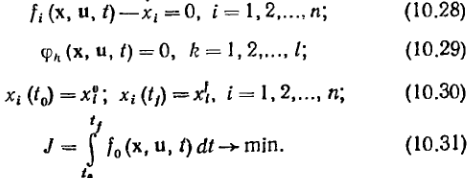, то найдутся такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера—Лагранжа (10.33) и (10.34)

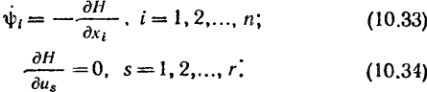. В соответствии с этим правилом, чтобы найти оптимальное управление и оптимальную траекторию, надо решить совместно уравнения (10.28), (10.29), (10.33) и (10.34) при краевых условиях (10.30). Уравнения Эйлера—Лагранжа получены при предположении, что управление u{t) является непрерывной функцией, а траектория х(t) — гладкой на интервале [t0,tj], Правило множителей Лагранжа остается справедливым и в том случае, когда u(t) принадлежит классу кусочно-непрерывных функций, а х(t) — классу кусочно-гладких функций. Только если оптимальное управление u(t) имеет разрыв 1-го рода в каких-либо точках (эти точки называются угловыми), то оно само и соответствующая ему траекторияx(t) должны удовлетворять указанным выше уравнениям лишь в точках непрерывности управления. В угловых точках должны выполняться так называемые условия Вейерштрасса—Эрдмана

(10.35)

где индексы «—» и «+» обозначают левый и правый пределы соответствующих функций.

Множители Лагранжа определяются с точностью до постоянного множителя. Действительно, они входят в уравнения Эйлера —Лагранжа линейно н однородно, и уравнения не изменяются, если все множители умножить на одно и то же постоянное число. Поэтому один из постоянных множителей Лагранжа, не равный нулю, можно приравнять любому отличному от нуля заданному числу. Условимся в неособом случае (ψ₀не равно 0) принимать ψ₀= —1. Дальше, если особо не оговаривается, будет подразумеваться неособый случай.

Для определения 2n+r+lнеизвестных xi,i= 1, 2, ...n, ψ_i,i=1,2,…nu_j,j=1,2,…rи λ_кк=1,2,….lимеется столько же уравнений. Но среди них имеется 2nдифференциальных уравнений, при решении которых появится 2nнеизвестных (постоянные интегрирования). Эти неизвестные можно найти из краевых условий (10.30), которые содержат 2nсоотношений. Таким образом, решение исходной вариационной задачи свелось к решению краевой задачи Коши.

Отметим еще раз, что уравнения Эйлера—Лагранжа являются только необходимым условием, т. е. любое решение исходной задачи является экстремалью, но не любая

экстремаль, удовлетворяющая граничным условиям, является решением. Но если решение задачи существует и экстремаль, удовлетворяющая граничным условиям, единственна, то,

очевидно, эта экстремаль и будет решением.

18. Задача Лагранжа на условный экстремум при конечных связях.

49. Система уравнений Эйлера – Лагранжа при конечных связях.

К вариационным задачам на условный экстремум относятся задачи, в которых требуется найти экстремум функционала, если на допустимые кривые кроме граничных условий накладываются условия иного типа, так называемые условия связи, которые могут быть заданы системами конечных или дифференциальных уравнений.

Рассмотрим вариационную задачу для функционала

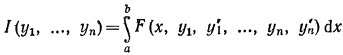(1)

Определенного на множестве функций, принадлежащих пространству С ⁽¹⁾с граничными условиями

(2)

Кроме того допустим, что функции у1, у2…удовлетворяют к уравнениям связи

(3)

Вариационная задача 1, 2, 3 называется задачей на условный экстремум с конечными связями. Рассмотрим решение методом Лагранжа

Теорема1. Если система функций

(4)

Удовлетворяющая граничным условиям 2 и условиям связи 3. Дает экстремум функционалу 1, то сущ-ют такие функции λj(x) (множители Лагранжа), что система функций 4 является экстремалью функционала

(5)

Вариация функционал 1 имеет вид

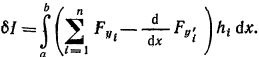(6)

Преобразуем вариацию 6 из уравнений связи:

Применяя к разности этих уравнений формулу Тейлора, умножая на функции множтителей и суммируя по j. Далее интегрируя в пределах от а до в и прибавляя интеграл к вариации 6 получим необходимое условие экстремума функционала

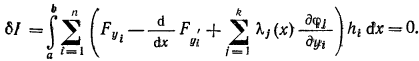(7)

По условию, функции независимы, поэтому существует якобиан порядка к, отличный от нуля. Пусть например,

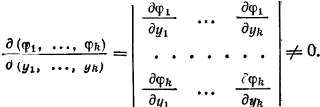
Отсюда следует, во-первых, что функции выражаются через функции, которые независимы, и, во-вторых, определитель системы уравнений

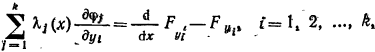(8)

Являющийся выбранным якобианом, отличен от 0. Следовательно, система 8 имеет решение . Подставив в равенство 7 найденные функции λ(х) приведем его к виду

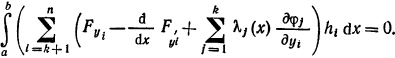
В этом равенстве приращения h_k+1,h_k+2,…h_nуже независимы. Поэтому, полагая всеh, кроме одного, равными 0 и применяя основную лемму вариационного исчисления, находим, что функции у удовлетворяют уравнениям

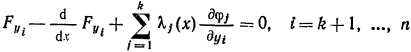
Объединяя эти уравнения с уравнением 8 получаем, что функции у(х) и λ(х) удовлетворяют системе уравнений

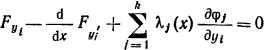(9)

Для всех i=1,2,..n. Система дифференциальных уравнений 9 является системой уравнения Эйлера для функционала 5. Кривые у – экстремали функционала. Для того чтобы найти экстремали вариационной задачи на условный экстремум (1-3) надо найти экстремали функционала 5, удовлетворяющие граничным условиям (2) и условиям связи (3). Таким образом, в задачах на условный экстремум требуется найтиnэкстремалей у1(х), у2(х),…у_n(х) и к множителей Лагранжа λ. Задача сводится к решению системы 9 изnдифференциальных уравнений второго порядка

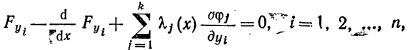
И к уравнений связи (3)

2nпроизвольных постоянных находятся из граничных условий 2.