26. Постановка задачи. Постановка задачи оптимального управления.

Общая постановка задачи оптимального управления

Задача синтеза оптимальных систем управления относится к классу задач оптимального управления и формулируется как вариационная задача. При этом кроме уравнения объекта управления должны быть заданы ограничения на управление и фазовый вектор, краевые условия и выбран критерий оптимальности.

Пусть уравнение объекта задается в нормальной форме

или в скалярном виде

где — фазовый вектор;— управление или вектор управления. Как отмечалось в гл. 2, любое уравнение, разрешимое относительно старшей производной, можно преобразовать к равносильной нормальной системе.

На управление и фазовый вектор еще могут быть наложены ограничения в виде конечных соотношений — равенств, неравенств. Их в общем виде можно записать так:

Здесь — некоторые заданные множества, зависящие, вообще говоря, от времени, причемт. е.Ut— подмножествоr-мерного пространства;X_t — подмножествоn-мерного пространства. В (10.2) первое соотношение называется ограничением на управление, второе соотношение — ограничением на фазовый вектор или фазовым ограничением. Ограничения на управление и фазовый вектор могут быть не разделены, и в общем случае они записываются в виде

Краевые (граничные) условия — ограничения на фазовый вектор в начальный и конечный tfмоменты времени в общем виде можно записать так:

Вектор х(tо) называют левым, а вектор х(tj) — правым концом траектории. Краевые условия имеют вид (10.3), если ограничения на левый и правый конец траектории разделены.

В противном случае они записываются в виде

Критерий оптимальности, который является числовым показателем качества системы, задается в виде функционала

Задача оптимального управления формулируется следующим образом: при заданных уравнении объекта управления (10.l), ограничениях (10.2) и краевых условиях (10.3) требуется найти такие программное управлениеu*(t) или управление с обратной связьюu*(х(t),t) и фазовую траекторию х*(t), при которых критерий (10.4) принимает минимальное (или максимальное) значение. Дальше для определенности примем, что функционал (10.4) минимизируется. Задачу максимизации выбором нового критерияJ1=-Jвсегда можно свести к задаче минимизации. Управленияи траектория х*(t) называются оптимальными. При решении задач синтеза оптимальных систем управления- обычно бывает достаточно найти оптимальное управление.

28. Уравнение Беллмана.

Принцип оптимальности. Уравнение Беллмана

Составление уравнения для функции Беллмана представляет собой второй основной этап решения задачи методом динамического программирования. На этом этапе могут применяться различные рассуждения, но все они в той или иной степени опираются на принцип оптимальности, который Беллман сформулировал следующим образом: оптимальная политика обладает тем свойством, что каковы бы ни были начальное состояние и принятое начальное решение, последующие решения должны составлять оптимальную политику относительно состояния, возникшего в результате первоначального решения. При составлении уравнения для функции Беллмана выявляется правильность инвариантного погружения. С другой стороны, способ погружения сказывается на виде уравнения. Обратимся к задаче (3) с заданными значениями параметров у, k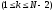и положим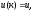гдеu- произвольный вектор из множестваU(k). Оставляя пока в стороне вопрос об оптимальности такого решения, постараемся распорядиться остальными переменнымиu(t),t= к +1,N-1, так, чтобы критерий качества принял минимально возможное значение, т. е. поставим перед собой следующую задачу:

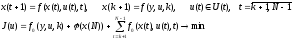
Согласно определению функции Беллмана минимальное значение критерия качества в этой задаче равно

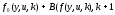(4)

Минимум выражения (4) по есть, очевидно, оптимальное значение критерия качества в задаче (3), т. е. В(у, к). Таким образом,

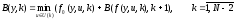(5)

Непосредственно из определения функции Беллмана следует

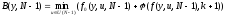(6)

Объединяя (5) и (6), получаем для функции B(y,k) рекуррентно-функциональное уравнение

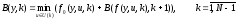( 7)

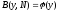(8)

которое называют уравнением Беллмана.

Из приведенных рассуждений также следует, что вектор u(y,k), на котором достигается минимум в (7), есть значение оптимального управления в задаче (3) в начальный момент времени.

Третий, заключительный, этап применения динамического программирования состоит в нахождении решения уравнения Беллмана и построении по нему оптимальной стратегии в исходной задаче. Решая рекуррентное уравнение (7), (8), последовательно получаем функции В(у, N), В(у, N -1),…, В(у, 1) и одновременно значения управления

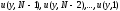(9)

на которых достигается минимум в (7). Понятно, что В(х₀,1) - минимальное значение критерия качества в исходной задаче (2). Оптимальные управление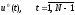и траектория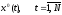рекуррентно вычисляются следующим образом:

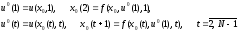(10)