1.1. Методы управления в условиях запаздывания |
19 |
|
|
r |
+ |
e |
+ |
R(s) |
u |
P0(s)e−sh |
y |
|
|
|
|
||||
|
– |
|
– |
|
|
|
|
|
|
|
|
|
|
+ |
ε |
|
|
|
|
|
|
– |
|
|
|
|
|
|
M0(s) |
e−sh |
|
|
|
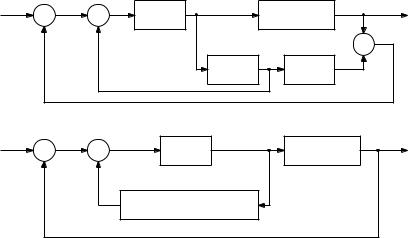
(а) Модифицированная структура предиктора Смита |
|
||||
r |
+ |
e |
+ |
R(s) |
u |
P0(s)e−sh |
y |
|
– |
|
– |
|
|
|
|
|
|
|
|
M0(s) − M0(s)e−sh |
|
|
|
|
|
(б) Модифицированная структура предиктора Смита |
|
||||
Рис. 1.4. Модификации системы управления с предиктором Смита
1.1.2Предиктор на основе метода М. Крстича
Линейным системам с входным запаздыванием посвящено огромное количество работ. Однако, остаются нерешенными такие задачи как системы с запаздыванием и по входу, и по состоянию, даже для линейного случая. При такой постановке классический подход становится неприменимым. Предиктор Смита расчитан только на асимптотически устойчивые объекты, так как не учитывает свободную составляющую движения системы, обусловленную ненулевыми начальными условиями.
Обозначенные задачи были решены всемирно известным ученым Мирославом Крстичом с помощью его метода бэкстеппинг (“backstepping” — обратный обход интегратора, [69]). Также данный метод позволил решить широкий спектр задач управления в условиях запаздывания, включая нелинейные системы, неустойчивые системы, неизвестное запаздывание, дополнительная динамика в системе, описываемая уравнениями в частных производных [67, 68, 70]. Под решением задачи понимается аналитическое доказательство (экспоненциальной) устойчивости замкнутой системы.
20 |
Глава 1. Обзор методов. Постановка задачи |
|
|
r |
e |
u |
P0(s)e−sh |
y |
+ |
K |
+ |
|
|
– |
|
+ |
|
|
|
|
e−sh |
|
|
|
|
1+sT |
|
|
|
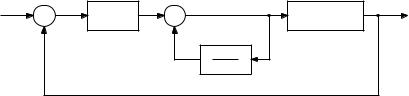
Рис. 1.5. Система управления с ППИ-регулятором |
|
||
Рассмотрим предиктор Крстича на наиболее простой задаче: стабилизация неустойчивой линейной системы с запаздыванием в канале управления. Дело в том, что более сложные задачи решаются с помощью этого же подхода с соответствующими модификациями: управление по выходу [90], управление бесконечномерными объектами, описываемыми уравнениями в частных производных и другие.
Рассмотрим линейный объект вида
_ |
(1.4) |
( ) = ( ) + ( − ), |
где R — вектор состояния, пара ( , ) полностью управляема, и управление ( ) запаздывает на секунд.
Нетрудно видеть, что для стабилизации системы (1.4) достаточно построить управление в виде
( − ) = ( ), |
(1.5) |
где вектор-строка обеспечивает гурвицевость матрицы + . Откуда имеем физически не реализуемый алгоритм управления
( ) = ( + ). |
(1.6) |
Тем не менее, используя решение для ( ) с учетом начальных условий, получим
( + ) = ( ) + ∫ − |
( − ) ( ) , |
≥ 0, |
(1.7) |
откуда имеем закон управления по состоянию |
|
|
|
( ) = [ ( ) + ∫ − ( − ) ( ) ], |
≥ 0, |
(1.8) |
|
1.1. Методы управления в условиях запаздывания |
21 |
|
|
который является реализуемым, хоть и является бесконечномер-
ным, так как содержит член с распределенным запаздыванием ∫ ( − ) ( ) . В замкнутом контуре исчезло запаздывание:
−
_ |
≥ . |
(1.9) |
( ) = ( + ) ( ), |
Выражение (1.9) справедливо только после секунд, а до этого момента состояние объекта изменяется по закону:
∫
( ) = (0) + ( − ) ( − ) . [0, ]. (1.10)
0
Закон управления вида (1.8) впервые был получен с позиций конечно-мерного представления системы [71,73] и редуцированного подхода [40]. На первый взгляд, такое интуитивно простое решение лежит на поверхности, однако вопрос о доказательстве устойчивости замкнутой системы остался без ответа. Проблема заключается в том, что в данном случае не удается применить функционал Ляпунова-Красовского и доказать устойчивость. Метод Крстича “backstpping” позволяет это сделать.
Запаздывание может быть представлено в виде уравнения в частных производных первого порядка
( , ) |
= |
( , ), |
(1.11) |
( , ) |
= |
( ), |
(1.12) |
где индексы и означают частную производную по соответствующему аргументу. Решение (1.11), (1.12) имеет вид
( , ) |
= ( + − ), |
(1.13) |
где выход блока запаздывания
(0, ) = |
( − ) |
(1.14) |
определяет запаздывающее управление (рис. 1.6). Рассмотрим бэкстеппинг преобразование [68]
∫
( , ) = ( , ) − ( , ) ( , ) − ( ) ( ), (1.15)
0
22 Глава 1. Обзор методов. Постановка задачи
U(t) |
|
|
|
U(t − D) |
|
|
|
X(t) |
|
|
|
e−sD |
X˙ (t) = AX(t) + BU(t |
− |
D) |
||||
u(D, t) |
|
|
u(0, t) |
|
|||||
|
|
|
|
|
|
|
|||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
D |
0 |
|
|
|
|
||||
|
|
|
|
|
|||||
Рис. 1.6. Линейный объект с запаздыванием в канале управления
которое позволяет преобразовать исходную систему (1.4), (1.11)– (1.14) в устойчивую целевую систему
_ |
( + ) ( ) + (0, ), |
(1.16) |
( ) = |
||
( , ) = |
( , ), |
(1.17) |
( , ) = |
0. |
(1.18) |
Рассчитывая производные ( , ) и ( , ) нетрудно найти решение для функций ( , ) и ( ):
( , ) = ( − ) , ( ) = . (1.19)
Подставляя ( , ) и ( ) в (1.15) и выбирая = , имеем закон управления
∫
( , ) = ( − ) ( , ) + ( ). (1.20)
0
Как и в редуцированном анализе (1.9) мы получили устойчивую систему (1.16), но при этом учтены начальные условия системы в виде возмущения (0, ). Заметим, что эта функция затухает в ноль
за секунд. Для доказательства экспоненциальной устойчивости системы (1.16) рассматривается функция Ляпунова [70]
|
|
|
|
|
|
|
|
||
( ) = ( ) ( ) + |
|
∫0 |
(1 + ) ( , )2 , |
(1.21) |
2 |
||||
где = > 0 — решение уравнения Ляпунова |
|
|||
( + ) + ( + ) = − |
(1.22) |
|||