2.1.1.Операции над высказываниями

1.Дизъюнкция (логическое “или”, “логическое сложение”). Наиболее популярные обозначения: и +.

2. Конъюнкция (логическое “и” “логическое умножение”). Наиболее популярные обозначения: ,и &.

3. Отрицание (логическое “не”). Наиболее популярные обозначения:и .

4. Импликация (логическое “если ... , то”, “влечет”) .

5. Эквивалентность (логическое “если и только если”) .

6. Неравнозначность (или “сумма по модулю 2”, или “исключающее или”) .

7. Штрих Шеффера (логическое “и-не”) |.

8. Стрелка Пирса (логическое “или-не”) .

Операции сведены в таблицу:

A	B			Ā				|	
0	0	0	0	1	1	1	0	1	1
0	1	1	0	1	1	0	1	1	0
1	0	1	0	0	0	0	1	1	0
1	1	1	1	0	1	1	0	0	0

Соглашение о старшинстве некоторых операций (по силе связывания):

, &, ,,.

2.1.2.Построение и анализ сложных высказываний

В качестве примера возьмем отрывок из Шолом-Алейхема (заимствованный, однако, у Д.А. Поспелова).

“... - Вот, что. Если вы хотите остаться у нас, если вы хотите, чтобы мы стали друзьями.

- Если вы не хотите, чтобы вам пришлось уезжать отсюда, то

- Забросьте книги под стол. Будем играть в шашки, в 66 или будем валяться на кровати и плевать в потолок...”

Придав конкретные значения отдельным элементарным высказываниям, можем определить истинность всего сложного высказывания для этого набора значений.

a - хочешь остаться в доме 1

b - хочешь остаться другом 0

с - захотеть уехать 0

d - забросить под стол книги 1

е - играть в шашки 0

f - играть в 66 1

g - валяться на кровати 1

h - плевать в потолок 0

a & b & (c)d & (efgh)

1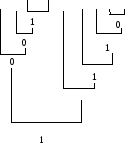0 0 1 0 1 1 0

1

Другой пример. Пусть на три входа "черного ящика" (х1, х2, х3) подаются (1) или не подаются (0) импульсы во всевозможных сочетаниях. На выходе (f) импульс либо появляется (1), либо отсутствует (0).

x1

x2

f

x3

Результаты замеров заносятся в «журнал исследований » - таблицу истинности.

Пусть она имеет следующий вид:

х1	x2	x3	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Что также можно записать в виде формулы:

f= x1x2x3x1x2x3x1x2x3x1x2x3

2.1.3.Алгебра высказываний

Сложные высказывания называются равносильными(f ≡g), если на одинаковых наборах значений элементарных высказываний они принимают одинаковые значения.

Законы :

1. Коммутативный.

A B≡BA AB≡BA

2. Ассоциативный.

A (BC)≡ABC A(BC)≡ABC

3. Дистрибутивный.

A BC≡(AB)(AC)

A(BC)≡ABAC

4. Де Моргана.

AB≡AB AB≡AB

5. Идемпотентности.

A A≡A AA≡A

6. Поглощения.

A (AB)≡A A(AB)≡A

7. Исключенного третьего. Противоречия.

AA≡1 AA≡0

8. A 1≡1 A1≡A

9. A 0≡A A0≡0

10. 0≡1 1≡0

11. A≡A

12. A B≡AB

13. AB≡ABAB

14. AB≡ABAB

15. A | B≡AB≡AB

16. AB≡AB≡AB

17. Операция склеивания.

ABAB≡A