7.10.Детерминированные автоматы с магазинной памятью (мп-автоматы)

Есть «промежуточная» математическая модель между автоматами и контекстно-свободными грамматиками – автомат с магазинной памятью. (МП-автомат).

Существует достаточно распространенная задача – задача определения парности скобок. Однако ее нельзя представить автоматной грамматикой.

Соответсвующая грамматика может выглядеть следующим образом:

S(S)

SSS

S

МП-автомат состоит из входной ленты, в ячейках которой записывается анализируемая строка (┤-конец строки), устройства управления и разбитого на ячейки магазина (стека).- символ пустого магазина. Устройство управления автомата может )."помнить" состояние (S1…).

Требуется распознать: ( ( ) ( ) )

( ( ) ( ) ) ┤



Работу автомата можно описать программой.

S1	X	
(	 X 	 X 
)		
┤		+

Здесь и далее используются обозначения:

 - поместить строку в вершину магазина.

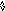 - заменить верхний символ магазина на строку.

 - убрать символ из вершины магазина.

 - сдвинуться на шаг вправо по входной строке.

>< - стоять на месте.

 - отвергнуть.

+ - принять.

S - State - состояние МП-автомата (на каждое состояние своя таблица, здесь одно состояние S1).

 [S1] ( ( ) ( ) ) ┤



x[S1] ( ( ) ( ) )┤



xx[S1] ( ( ) ( ) )┤



x[S1] ( ( ) ( ) )┤



xx[S1] ( ( ) ( ) )┤



x[S1] ( ( ) ( ) )┤



 [S1] ( ( ) ( ) ) ┤



Задача распознавания вложенных скобок "типа матрешка" сложнее и для ее распознавания требуется МП-автомат с двумя состояниями:

( ( ( ) ) )

S2	X	
(		
)	S2	
┤		+

S1	X	
(	S1X 	S1X 
)	S2	
┤		+

При встрече первой закрывающей скобки МП автомат меняет состояние S₁ на состояние S₂.

7.11.Транслирующие грамматики

В этих грамматиках присутствует элемент аттракциона - транслирующая грамматика не только анализирует входное слово: но и транслирует его. В большинстве практических случаев эти процессы разделяют, поэтому-то такие грамматики можно рассматривать как некий казус.

1. E E + T. 1. EE + T{+}.

2. E T. 2. ET.

3. T T * P. 3. TT * P{*}

4. T P. 4. TP.

5. P (E). 5. P(E).

6. P a. 6. Pa{a}.

7. P b. 7. Pb{b}.

8. P c. 8. Pc{c}.

Проанализируем строку

(a + b) * c

1. E TT * PP * P(E) * P(E + T) * P.

E TT * P{*}P * P{*}

(E) * P{*} (E + T{+}) * P{*}(a{a} + b{b}) * c{c}{*}

Если выделить символы, заключенные в фигурные скобки, то получится исходное выражение, оттранслированное в постфиксную запись.

ab + c *