2.8. Примеры неклассических логик

Различных видов логик уже создано очень много, начиная с древнеиндийской логики Навья-Ньяя и вышеупомянутой системы Аристотеля. Всякая логика ограничена. Невозможно создать универсальную логику, исчерпывающую все возможные потребности. Поэтому и создаются все новые логики.

Одна из наиболее популярных неклассических логик последние двадцать лет - это нечеткая (fuzzy) логика. Нечеткая математика базируется на нечетком отношении

принадлежности Например:Доцент Сидоров к множеству лысых, можно сказать, практически и не принадлежит!

А также на понятии лингвистической переменной. Например, лингвистическая переменная возрастможет иметьлингвистические значения:очень молодой, молодой, средних лет, пожилой, старый,…

Рассуждения в нечеткой логике могут быть типа:

Если немного добавить соли, то будет гораздо вкуснее.

Разумеется, для машинной обработки необходимо отобразить эти нечеткие понятия на "числовые оси", что осуществляется с помощью подбираемых функций принадлежности 

В нечеткой логике не выполняются закон исключенного третьего и закон противоречия.

Модальные логики.

Модальность - дополнительная характеристика, приписываемая высказыванию.

Пусть A - высказывание.

A - необходимо А.

А - возможно А.

Если. А = 0, то А = 0

Если А = 1, тоА = 1.

Но если А = 1*, тоА может быть истинно или ложно.

Скажем, «Вася ловит рыбу» - истинно, но «Необходимо, что Вася ловит рыбу» – ложно, поскольку Вася это делает только по настроению.

Например, «Летом выпал снег» – может быть ложным высказыванием, а «Возможен случай, что летом выпадет снег» - истинным.

Но если

0, если противоречит (физическим) законам.

1, иначе.

{

А = 0, то А =

Например, «2 + 2 = 5» - ложно и «возможно, что 2 + 2 = 5» – также ложно, но

«Вася стреляет» – ложно, но «Вася может и пострелять» – истинно (особенно, когда деньги кончились, а курить охота).

Существует достаточно большое количество разновидностей модальных логик.

Некоторые возможные соотношения в модальных логиках:

¬P =¬PP¬P=1

¬P =¬PP&¬P=1

¬¬P =P

¬¬P =P

Некоторые возможные аксиомы:

А А

А А

(А В)(АВ)…

Немонотонные логики. Кратко суть таких логик формулируется следующим образом: добавление в систему новых аксиом может привести к изменению уже существовавших…Они хороши тем, что часто следуют принципу:Если не нравится полученный в процессе вывода результат - можно изменить исходные посылки.

Существует много весьма разноплановых немонотонных логик.Например, вывод

C(x, y) & Г(y)=z :Г(x) = z |Г(x) = z

То есть из фактов, что C(x, y) - "x,y - супруги", . Г(y)=z - "город, где проживает y. называется z". Символ « : » отделяет условие от предложения.

и Г(x) = z - "x живет в городе z" не противоречит существующим аксиомам, то.

в этой системе выводимо Г(x) = z, что "x живет в городе z".

Индуктивные логики.Это логики правдоподобных рассуждений "от частного к общему". Когда Шерлок Холмс по отдельным уликам восстанавливал картину преступления, то егодедуктивный методбыл чистой водыиндуктивным методом.

Это элементарно, Ватсон!

Поскольку правдоподобные рассуждения не гарантируют стопроцентно правильность логического заключения (у Холмса результат был близок к 100%, хотя и у него бывали ошибки), то можно говорить о большей или меньшей правдоподобности результата.

Пусть Аозначает "А более правдоподобна", тогда можно предложить, например, такие индуктивные правила вывода:

A B, B |A

A B, CB |A ~ C

A

A | D

& B |D

A & C |D

Эротетические логики.Так названы логикивопросов и ответов.

Правильно поставленный вопрос - это такой вопрос у которого предпосылка истинна и не противоречива.

В рамках этой логики доказана полезная для повседневной практики теорема:

На глупый вопрос нельзя дать умный прямой ответ.

Два основных типа вопросов:

уточняющие (типа .ли),

воспроизводящие (типа что ).

Вопросы могут быть простыми и сложными.

А ответы могут быть:

- истинные и ложные,

- прямые и косвенные,

- краткие и развернутые,

- полные и неполные.

Временные логики :

Высказывание А,

Р_А- "было А"

F_A- "будет A"

A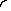B - "если А, то после этого В".