
Курсовые / много всякого / виды графов
.docвведем терминологию, а заодно сравним ориентированные и неориентированные графы гносеологически, представив параллельные места билингвой - в виде следующей таблицы. Орграф здесь и далее - ориентированный граф.
ГРАФЫ И ОРИЕНТИРОВАННЫЕ ГРАФЫ (АНАЛОГИИ И ОТЛИЧИЯ)
|
Пусть D = (V, A) - орграф |
Пусть G = (V, E) - граф |
|
Путь в D - последовательность вершин и дуг u1, a1, u2, a2,..., ut, at, ut+1 , где t 0, причем каждая вершина ui V, а каждая дуга ai A, и ai всегда является дугой (ui, ui+1). Путь обычно записывается последовательностью вершин u1, u2, ..., ut, ut+1. |
Цепь в G - последовательность вершин и ребер u1, e1, u2, e2,..., ut, et, ut+1, где t 0, причем каждая вершина ui V, а каждое ребро ei E, и ei всегда является ребром (ui, ui+1). Цепь обычно записывается последовательностью вершин u1, u2, ..., ut, ut+1. Цепь = маршрут без повторений (каждое ребро проходится лишь один раз). |
|
Полупуть в D - последовательность вершин и дуг u1, a1, u2, a2,..., ut, at, ut+1, где t 0, причем каждая вершина ui V, а каждая дуга ai A, и ai всегда является либо дугой (ui, ui+1), либо дугой (ui+1, ui). Полупуть также обычно записывается последовательностью вершин u1, u2, ..., ut, ut+1. |
Аналогия - та же цепь (см. Выше)
В определении полуцепи нет смысла - полуцепь всегда совпадает с соответствующей цепью.
|
|
Полный путь или полный полупуть в D - путь или полупуть, проходящий через все вершины D. |
Полная цепь или полная полуцепь в G - цепь или полуцепь, проходящая через все вершины G. |
|
Простым путем или простым полупутем в D называется путь или полупуть без повторяющихся вершин. |
Простой цепью в G называется цепь без повторяющихся вершин. |
|
Замкнутым путем или полупутем в D называется путь или полупуть u1, a1, u2, a2,..., ut, at, ut+1, в котором ut+1=u1. |
Замкнутой цепью в G называется цепь u1, u2, ..., ut, ut+1, в которой ut+1=u1. |
|
Полный замкнутый путь или полный замкнутый полупуть в D - полный путь или полный полупуть, который замкнут. |
Полная замкнутая цепь в G - полная цепь, которая замкнута. |
|
Контуром в D называется замкнутый путь u1, u2, ..., ut, u1, в котором все вершины различны. |
Циклом в G называется замкнутая цепь u1, e1, u2, e2,..., ut, et, u1 , в которой все вершины различны. |
|
Полуконтуром в D называется замкнутый полупуть, u1, a1, u2, a2,..., ut, at, u1, в котором все вершины u1, u2, ..., ut и все дуги a1, a2,..., at различны. |
Аналогия - тот же цикл (см. Выше)
В определении полуцикла нет смысла - полуцикл всегда совпадает с соответствующим циклом. |
|
Вершинаui, достижима из вершины uj, если имеется путь из ui в uj. |
Вершинаui, достижима из вершины uj, если имеется соединяющая их цепь. |
|
Вершиныui и uj соединимы, если имеется путь из вершины ui в вершину uj или из вершины uj в вершину ui. |
Вершиныui и uj соединимы, если имеется соединяющая их цепь. |
|
Длиной пути, полупути, простого пути, простого полупути, контура или полуконтура называется число дуг, содержащихся в них. |
Длиной цепи, простой цепи или цикла называется число ребер, содержащихся в них. |
|
Расстояние d(ui, uj) от вершины ui и до вершины uj в D равно длине кратчайшего пути из ui в uj или не определено, если путь из ui в uj отсутствует. Во взвешенном графе длиной и расстоянием обычно называют с учетом веса ( весов). |
Расстояние d(ui, uj) от вершины ui и до вершины uj в G равно длине кратчайшей цепи между ui и uj или не определено, если цепь между ними отсутствует. |
ПОДГРАФЫ, ОРИЕНТИРОВАННЫЕ ПОДГРАФЫ И СВЯЗНОСТЬ
(АНАЛОГИИ И ОТЛИЧИЯ)
|
Пусть D=(V, A) - орграф |
Пусть G=(V, E) - граф |
|
Орграф D называется сильно связным (сильным, категории связности 3), если для каждой пары вершин ui и uj в Dui достижима из ujи ui достижима из ui. |
Граф G называется связным, если каждая пара вершин ui и uj в Gсвязана цепью. |
|
Орграф D называется слабо связным (слабым, категории связности 1), если каждая пара вершин ui и uj в D соединима (полупутем). |
Аналогия - см. выше
|
|
Орграф D называется односторонне связным (односторонним, категории связности 2), если для каждой пары вершин ui и ujв D либо ui достижима из uj , либо uj достижима из ui . |
Аналогия - см. выше
|
|
Подграфом в D называется орграф (W, B), в котором W V, B A. |
Подграфом в G называется граф (W, F), в котором W V, F E. |
|
Порожденным подграфом в D называется подграф (W, B), в котором B содержит все дуги из A, соединяющие вершины в W. |
Порожденным подграфом в G называется подграф (W, F), в котором F содержит все ребра из E, соединяющие вершины в W. |
|
Сильной компонентой в D называется максимальный сильно связный (порожден-ный) подграф. |
Компонентой (связности) в G называется максимальный связный (порожденный) подграф. |
Взвешенный граф, взвешенный орграф - граф (орграф), каждому ребру которого приписан некоторый вес.
Знаковый граф, знаковый орграф - граф (орграф), каждому ребру которого приписан некоторый знак.
Знак пути, цепи, замкнутого пути, замкнутой цепи, контура, цикла и т.д. определяется как произведение знаков входящих в них дуг или ребер, если знак плюс заменить на +1, а знак минус на -1. Очевидно, что путь, цепь и т.д. имеют знак минус, если число дуг или ребер, содержащихся в них, нечетно, иначе они имеют знак плюс.
Пример:
Хейдер изучал задачи из области социологии малых групп людей (Heider F. Attitudes and Cognitive Organization. - J. of Phych., 21, 1946, p. 107-112).
Его результаты - полный обзор вариантов знаковых графов для группы из трех человек в условиях явно выраженной выраженной симпатии / антипатии представлены на рисунках.
Группы из трех лиц по Хейдеру психологически
сбалансированные

несбалансированные
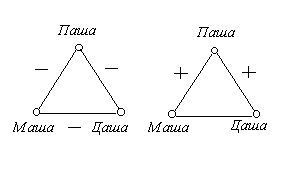
Анализ этого и огромного количества других примеров из самых разных областей человеческой деятельности привел Картрайта и Харари (Cartwright D. and Harary F. Structural Balance: A Generalization of Heider's Theory. - Psych. Rev., 63, 1956, p. 277-293) к следующей математической модели баланса:
Малая группа является сбалансированной, если представляющий ее знаковый граф сбалансирован.
Знаковый граф называется сбалансированным, если каждый цикл в нем положителен.
Теорема о структуре (теорема Харари о балансе)
Для знакового графа G=(V,E) следующие утверждения эквивалентны:
-
Граф G сбалансирован.
-
Каждая замкнутая цепь в G положительна.
-
Любые две цепи между любыми двумя вершинами ui и uj имеют одинаковый знак.
-
Множество вершин V можно разбить на два подмножества A и B так, что каждое положительное ребро соединяет вершины одного подмножества и каждое отрицательное соединяет вершины различных подмножеств.
Последнее утверждение называют также критерием баланса.
