4.4. Деревья

Дерево - это связный граф без циклов. Можно дать другое определение дерева или вывести его из первого. Дерево – это граф, между любой парой вершин которого существует единственная цепь.

Теорема: В графе типа дерева с n вершинами n-1 ребер.

Доказательство. Для графа, состоящего лишь из одной вершины, это соотношение выполняется. Пусть оно выполняется и для графа с n-1 вершинами, тогда добавление новой дуги приводит к добавлению и одной вершины, что сохраняет соотношение.

П римеры деревьев.

Лесом называется граф, состоящий из нескольких компонент связности, каждая из которых является деревом.

Диаметром для графов типа дерева является максимальное расстояние между его вершинами.

. Определим для каждой вершины ее расстояние от самого удаленного листа Минимальное число - радиус, эта вершина корневая (центральная).

В любом дереве существует одна или две (смежные) корневые вершины

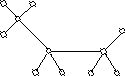4 4

4

4

2 3

-Диаметр 4.

3 3 4 4

4 3 3 4

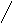
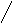
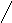
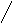
Диаметр: 5

Радиус : 3

5 5 4 4 4 4 5 5

4.5. Алгоритм Краскала

Пусть дан полный граф. Ребрам приписаны штрафы. На основе этого графа строят дерево, имеющее минимальный суммарный штраф.

Для этого на каждом шаге выбирают ребро, имеющее минимальный штраф и не образующее цикл с уже выбранными ребрами.

.

Пример.

2 3 5 5

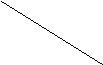
6

4 4 8 6

6

Жирными линиями выделено минимальное дерево

Теорема Кэли для раскрашенных деревьев.

Для n вершин существует n^n-2 различных помеченных деревьев.

Например, существует 16 различных деревьев с четырьмя вершинами.

1 2 3 4

4 3 2 1

4 вершины  4^{4 - 2} = 16 различных помеченных деревьев

1 2 3

4

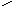
4.6. Планарные графы

Граф - плоский, если он изображен на плоскости без пересечения ребер.

Граф - планарный, если он может быть изображен на плоскости без пересечения ребер.

Л юбой плоский граф может быть преобразован в граф с прямыми ребрами.

 

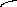
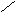
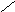
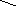
неплоский, но плоский плоский с

планарный прямыми ребрами

Граф, где все вершины соприкасаются с внешней гранью - внешнепланарный.

Два "замечательных" непланарных графа:

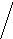
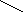
К₅ К_3,3

Приведем без доказательства две теоремы:

Любой граф, содержащий в качестве подграфа К₅ или К_3,3 - непланарен.

Два графа гомеоморфны если они тождественны с точностью до вершин со степенью =2.

Любой граф, содержащий в качестве подграфа граф гомеоморфный К₅ или К_3,3 или - непланарен.

Теорема (Эйлера для планарных графов):

В любом планарном графе

В + Г = Р + 2.

где: В - число вершин

Г - число граней

Р - число ребер

Доказательство:

1 + 1 = 0 + 2

2 + 1 = 1 + 2

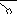3 + 2 = 3 + 2

4 + 2 = 4 + 2

Пусть есть граф с n вершинами, для которого это соотношение верно.

Добавление ребра приводит к увеличению на едитницу либо числа граней, либо вершин.