с инета для метод

dq = σdS = σ R dR dφ. Соответственно напряженность поля от этого точечного заряда в точке c координатой z0 будет равна

Разложим dE на две составляющие – по оси Z и перпендикулярную оси Z. Последняя при суммировании по площади диска в силу симметрии задачи даст нуль, а первая будет равна

dEz = dEcosϑ, где cosϑ = z0 . Тогда r

Замечание. Тот же результат можно получить гораздо легче, используя решение базовой задачи 1.3.5. Для этой цели выделим в плоскости диска малое кольцо радиуса r, которое будет нести заряд dq = σ dS = σ 2π r dr и которое, согласно решению задачи 1.3.5, создаст на оси диска напряженность поля, равную по величине

Интегрируя это выражение по r от нуля до R0, получаем искомый ответ.

Задача 1.3.7. Заряд равномерно распределен по поверхности полусферы радиуса R с поверхностной плотностью заряда σ. Определить напряженность электрического поля в центре полусферы.

Задачи этого раздела в большинстве своем являются базовыми. В дальнейшем результаты решения этих задач неоднократно будут использованы при решении задач других разделов.

Задача 1.3.8 (базовая задача). Найти в произвольной точке напряженность поля, создаваемого положительным зарядом, равномерно распределенным с поверхностной плотностью σ на бесконечной плоскости.

Решение

Поскольку плоскость бесконечная, распределение зарядов и поля обладает плоской симметрией. Следовательно, линии напряженности поля везде направлены по нормали к плоскости и, следовательно, параллельны друг другу, а модуль напряженности одинаков во всех точках, отстоящих от плоскости на одно и то же рас-

находящийся внутри замкнутой поверхности этого цилиндра, равен

Напряженность поля не зависит от расстояния от плоскости. Это однородное поле, силовые линии которого начинаются на заряженной плоскости и уходят на бесконечность, оставаясь перпендикулярными к заряженной плоскости.

Тот же результат получится и для отрицательного заряда. В этом случае силовые линии поля начинаются в бесконечности и заканчиваются на заряженной плоскости.

Конечно, бесконечных заряженных плоскостей в природе не существует. Однако полученный результат можно использовать для определения напряженности поля вблизи равномерно заряженной пластины, когда расстояние от точки наблюдения до пластины много меньше размеров пластины и, кроме того, точка наблюдения находится достаточно далеко от края пластины. Чем лучше выполнены эти условия, тем точнее полученная формула определяет напряженность поля в точке наблюдения. Это типичный пример придания физического смысла результатам расчета напряженности поля от объекта бесконечной протяженности.

Отметим, что на заряженной поверхности напряженность поля Е не определена (испытывает скачок). Это связано с выбором модели поверхности как не имеющей толщины. В реальных материалах электрическое поле вблизи заряженной поверхности меняется очень быстро на расстояниях порядка нескольких атомных слоев. В этой области модель не имеющей толщины поверхности оказывается слишком грубой и требует уточнения с учетом свойств составляющих ее атомов и молекул. В дальнейшем, говоря о скачке напряженности, мы будем иметь в виду именно такую картину.

σ

Ответ: E = 2ε0 .

Задача 1.3.9. Две бесконечные параллельные друг другу плоскости равномерно заряжены с поверхностными плотностями заряда σ1 и σ2. Найти распределение напряженности поля: а) когда заряды одного знака, б) когда заряды разных знаков.

Решение

Напряженности полей, создаваемых каждой плоскостью, найдены в базовой задаче 1.3.8. Используем полученные там решения и принцип суперпозиции. На рис.1.10 схематически показаны поля от каждой плоскости для случаев а) и б); при этом положительным направлением напряженности считается направление слева направо (именно это направление будем считать положительным направлением оси Х).

а) В области 1 поля E1 и E2 сонаправлены, поэтому E(1) = –E1 – E2= –(E1 + E2).

В области 2 направления полей противоположны, поэтому

E(2) = –E2 + E1.

Аналогично в области 3 имеем

E(3) = E1 + E2.

Рис.1.10. Напряженности электрических полей, создаваемых двумя равномерно заряженными плоскостями (задача 1.3.9): а) заряды плоскостей одного знака; б) заряды плоскостей противоположных знаков

Если плотности зарядов одинаковы и равны σ, то проекции векторов напряженностей на ось Х будут равны:

б) Рассмотрение аналогично пункту а). Находим:

E(1) = E2 – E1; E(2) = E1 + E2 ; E(3) = E1 – E2.

В случае одинаковых по модулю зарядов имеем

E(1) = E(3) = 0, E(2) = σ .

ε0

Как и в задаче 1.3.8, полученные результаты можно использовать для пластин конечных размеров в точках пространства, находящихся достаточно близко к плоскостям пластин и отстоящих достаточно далеко от краев пластин. Фактически расстояния между пластинами должны быть малыми по сравнению с размерами пластин, а точка наблюдения находиться далеко от краев пластин. В противном случае отклонения от полученных результатов становятся существенными (поле искажается за счет краевых эффектов).

Ответ: В областях (1), (2) и (3) поля однородные и их напряженности соответственно равны:

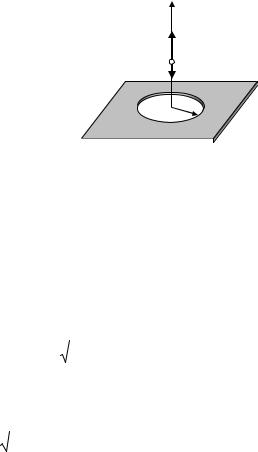
Задача 1.3.10. В бесконечной тонкой плоскости, заряженной равномерно с поверхностной плотностью заряда σ, вырезано круглое отверстие радиусом R. Найти напряженность электрического поля на оси этого отверстия (рис. 1.11, для наглядности плоскость показана в виде тонкой пластины).

где z0 – расстояние от точки наблюдения до плоскости. Окончательный ответ получаем, складывая эти две напряженности.

Задача 1.3.11. Определить напряженность поля Е внутри и вне безграничного плоского слоя толщиной 2h, в котором равномерно распределен положительный заряд с объемной плотностью ρ.

Решение

В силу симметрии задачи вектор напряженности может быть направлен только перпендикулярно плоскости (ось Х). Для применения теоремы Гаусса (1.10) выбираем расположенный симметрично относительно центральной плоскости слоя цилиндр с осью, параллельной оси Х, площадью основания S и длиной образующей 2x

(рис. 1.12).

Рис. 1.12. Поверхность Гаусса для равномерно заряженного плоского слоя (задача 1.3.11): а) вычисление напряженности внутри слоя; б) вычисление напряженности вне слоя

Если x < h, то теорема Гаусса определяет напряженность поля внутри заряженного слоя, если x > h – снаружи. Рассуждения проводятся в точности аналогично базовой задаче 1.3.8. При x < h (рис. 1.12а) получаем

При x > h (рис. 1.12б) имеем

Внутри слоя величина напряженности поля нарастает от центра слоя по линейному закону, а вне слоя поле становится однородным, как в случае бесконечной заряженной плоскости. Как и в предыдущих двух задачах, решение для конечного по площади слоя справедливо в области, где можно пренебречь краевыми эффектами.

нее из выражения напряженности поля вне цилиндра находим поле для бесконечной нити:

E = τ 1 . 2πε0 r

Конечно, этот результат можно получить и сразу из теоремы Гаусса, так как заряд внутри вспомогательного цилиндра равен в этом случае τh, а поток вектора E через боковую поверхность цилиндра

даче 1.3.3, как предельный случай напряженности поля от нити конечной длины.

Задача 1.3.13. В круглом бесконечном цилиндре радиуса R равномерно распределен положительный заряд с объемной плотностью ρ. Найти напряженность электрического поля в произвольной точке.

Решение

Для применения теоремы Гаусса (1.10) выбираем поверхность Гаусса в виде цилиндра, как в задаче 1.3.12 (рис. 1.13).

Для области внутри цилиндра r < R заряд внутри поверхности Гаусса равен ρπr2h, а поток вектора E через поверхность равен

2πrhE. По теореме Гаусса получаем Eвнутри = 2ρε0 r . Внутри заря-

женного по объему цилиндра напряженность поля нарастает от нуля на оси цилиндра по линейному закону, достигая на его поверх-

ности значения ρR . Напряженность поля является здесь непре- 2ε0

рывной функцией от r, так как нет заряженных поверхностей с плотностью σ ≠ 0.

Для области вне цилиндра r > R заряд внутри поверхности Гаусса равен ρπR2h, поток вектора E равен 2πrhE, и по теореме Гаусса

Eвне = ρR2 1 . Устремляя здесь r → R, убеждаемся в непрерывности 2ε0 r

функции E(r).