с инета для метод

§6.2. Основные типы задач (классификация)

6.1.Определение сопротивления, электрических полей, напряжений и тока утечки в сплошной среде.

6.2.Определение теплоты, выделяющейся в проводнике (среде), при протекании тока.

6.3.Расчет цепей квазилинейных проводников.

6.4.Расчет разветвленных цепей, сводимых к неразветвленным благодаря элементам симметрии.

§6.3. Методы решения и примеры решения задач

Задачи типа 6.1

Определение сопротивления, электрических полей, напряжений и тока утечки в сплошной проводящей среде

Метод решения. При рассмотрении токов в проводящих средах и нахождении сопротивления среды между электродами целесообразно придерживаться следующей схемы решения задачи (электрод – эквипотенциальный проводник, электропроводность которого много больше электропроводности среды).

Для расчета сопротивления по закону Ома нужно найти отношение напряжения на электродах U и полного тока I через систему.

В качестве исходного параметра удобнее всего взять полный ток I, поскольку величины зарядов на электродах заранее могут быть не очевидны.

а) Начать решение целесообразно с нахождения плотности тока j(r), поскольку при протекании постоянного тока для j(r) всегда соблюдается соотношение (6.2) div j = 0, независимо от особенностей диэлектрических и проводящих свойств среды. С другой стороны, j(r) легко связать с полным током через электрод соотношением (6.4). В задачах с симметрией условие (6.2) обычно позволяет сразу определить характер зависимости плотности тока j от координат.

б) Далее, пользуясь дифференциальным законом Ома (6.3), перейти к напряженности электрического поля E(r) = ρ(r) j(r).

в) Зная Е(r), интегрированием можно найти разность потенциалов (напряжение) между электродами 1 и 2:

182 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

(2)

U = − ∫E(r)dr .

(1)

Используя закон Ома (6.5), определить сопротивление среды между электродами

R = U .

I

Таким образом, задача решается в следующей последовательности:

Если проводящая среда однородна, то поле полностью определяется зарядами и потенциалами электродов, и можно исходным параметром взять напряжение на электродах и решать в обратной последовательности:

или же исходить из свободного заряда на электродах ±q и решать по схеме:

Однако в случае неоднородной проводимости среды простой переход U → E или q → E невозможен. Поле Е будет определяться при этом не только геометрическими факторами и напряжением U или зарядом электродов q, но и характером зависимости ρ(r) из-за появления в проводящей среде ненулевой плотности свободных зарядов.

Задача 6.3.1. На плоский конденсатор ёмкостью С подано постоянное напряжение U. Найти ток утечки через конденсатор, если удельное сопротивление однородного вещества, которым заполнен зазор между обкладками конденсатора, равно ρ, а диэлектрическая

проницаемость равна ε.

Решение

Так как напряжение на обкладках конденсатора постоянно, а среда, заполняющая пространство между его обкладками, однородна, то для нахождения тока утечки, текущего через конденсатор можно воспользоваться схемой (6.17).

184 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

j1 = j2= j = I .

S

Из закона Ома в дифференциальной форме (6.3) получаем напряженности полей в слоях 1 и 2:

E1 = ρ1 j, E2 = ρ2 j.

Ввиду однородности полей для напряжения между обкладками конденсатора получим

U = ϕ1 − ϕ2 = E1d1 + E2d2 = j(ρ1d1 +ρ2d2),

откуда находим плотность тока и полную силу тока через конденсатор

Используя закон Ома (6.5), найдем сопротивление данного слоистого конденсатора

R = U = ρ1d1 + ρ2d2 .

IS

2)Для нахождения заряда пластин можно воспользоваться граничным условием для нормальной компоненты вектора электрического смещения

D2n – D1n = σ,

где σ – поверхностная плотность свободных зарядов, n – вектор нормали в направлении сред 1 → 2. Учитывая, что вне конденсатора D = 0, для левой пластины получим

σ1 = D1 = ε0ε1E1,

для правой пластины

σ2 = –D2 = –ε0ε2E2.

Напряженности полей E1 и E2 легко найти из найденной плотности тока:

Далее можно определить полный заряд каждой из пластин:

186 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

водниками, их можно рассматривать как электроды с равными по модулю зарядами +q и –q и решать задачу согласно схеме 6.18.

Согласно теореме Гаусса ((1.10), глава 1) напряженность электрического поля в пространстве между сферами (a < r < 2a) равна

Определим силу тока, текущего в такой системе. Так как заряды на электродах постоянны, то через любую поверхность (концентрическую сферу радиуса a ≤ r ≤ 2a) сила тока одинакова и равна

ρ

Ответ: R = 8πa .

Замечание 1. Сопротивление безграничной среды с удельным сопротивлением ρ, окружающей уединенную проводящую сферу

ρ

радиуса а, равно R∞ = 4πa , так как в этом случае r2→∞.

Замечание 2. Используя связь между сопротивлением однородной среды и её ёмкостью данную задачу можно решить короче. Так как ёмкость сферического конденсатора равна (см. (3.9) главы 3)

Задача 6.3.4. Доказать справедливость соотношения (6.7), то есть показать, что сопротивление однородной проводящей среды, заполняющей всё пространство, между двумя идеально проводя-

щими телами произвольной формы, равно R = εε0 . Здесь С – ём-

λC

кость системы, λ – удельная электропроводность вещества, ε – его диэлектрическая проницаемость.

Решение

Ввиду однородности среды будем следовать схеме (6.18). Пусть проводники (электроды) заряжены одинаковыми по величине, но разными по знаку зарядами ± q , а напряжение между ними

U = q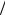C .

Вектор электрической индукции вблизи поверхности каждого проводника перпендикулярен поверхности и равен D = σ (где σ – поверхностная плотность свободного заряда на проводнике). Напряженность электростатического поля вблизи поверхности

E = D = σ . εε0 εε0

Согласно закону Ома в дифференциальной форме (6.3) вектор плотности тока параллелен вектору напряженности поля и поэтому вблизи поверхности проводников перпендикулярен поверхности и

λσ

по модулю равен j = jn = λE = εε0 .

Силу тока через электрод можно найти интегрированием плотности тока по поверхности электрода

Замечание. Поместим в однородную проводящую среду, заполняющую всё пространство, локализованный заряд объёмной плотности ρ0. Электрическое поле, создаваемое этим зарядом, вызовет ток плотности j = λE, который будет уменьшать объёмную плот-

j = λE = λ U . l

Таким образом, плотность тока в слое толщины dr, находящемся на расстоянии r от оси Z, будет равна

j = λ U = αUr2 . l l

Согласно (6.4) найдем полную силу тока

Задача 6.3.6 (базовая задача). Зазор между обкладками плоского конденсатора заполнен веществом с диэлектрической проницаемостью ε и с удельной проводимостью, меняющейся в направлении, перпендикулярном к обкладкам, по линейному закону от λ1 до λ2. Площадь пластин S, ширина зазора d. На конденсатор подано напряжение U.

Найти: 1) ток I через конденсатор; 2) заряды пластин q1 и q2; 3) заряд конденсатора q; 4) плотность свободных зарядов ρсвоб(x) внутри зазора; 5) плотность связанных (поляризационных) зарядов ρ′(x) в среде; 6) полный свободный заряд в среде qсвоб.

Решение

Ввиду неоднородности среды в направлении протекания тока воспользуемся схемой (6.16).

Запишем линейный закон изменения удельной проводимости λ (x) = λ1 + αx. Для нахождения α подставим граничное условие:

λ(d) = λ1 + αd = λ2 . Отсюда получаем, что α = λ2 − λ1 , и d

190 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

λ(x) = λ1 + λ2 − λ1 x . d

В плоском конденсаторе плотность тока везде однородна и постоянна j = I / S = const. Однако напряженность электрического поля

Согласно закону Ома (6.5) сопротивление конденсатора равно

Заряды пластин определим аналогично задаче 6.3.2 из граничных условий для вектора электрического смещения, величина которого в среде

на правой пластине (x = d):

Полный заряд q, получаемый конденсатором при зарядке, равен большему по модулю из зарядов пластин: q = max (|q1|, |q2|).

Объемную плотность свободных зарядов в среде можно найти

как