с инета для метод

5.4.4. Внешняя обкладка воздушного сферического конденсатора может симметрично сжиматься. После сообщения обкладкам заряда ±q, внешняя обкладка под действием сил притяжения сжалась так, что её радиус уменьшился от а, до b. Радиус внутренней обкладки остался неизменным. Найти работу, совершенную силами притяжения.

5.4.5. Центр незаряженной проводящей сферы радиуса а расположен на плоской границе двух изотропных диэлектриков с проницаемостями ε1 и ε2, вплотную прилегающих к сфере и заполняющих всё пространство вне сферы. На расстоянии b < a от центра сферы находится точечный заряд q. Определить энергию поля вне сферы.

q2

Ответ: W = 4πε0 (ε1 + ε2 )a .

5.4.6. Точечный заряд q расположен на оси симметрии плоского воздушного заряженного конденсатора (вне его) на расстоянии L от центра положительной обкладки, и на расстоянии L + d от центра отрицательной. Обкладки конденсатора – квадраты с ребром а. Напряжение на конденсаторе U.

Оценить силу, с которой конденсатор действует на заряд, если L >> a.

5.4.7. Пространство внутри плоского конденсатора полностью занимает пластина из твердого диэлектрика с проницаемостью ε. Найти минимальную работу, которую необходимо совершить, чтобы увеличить расстояние между пластинами конденсатора вдвое, если он всё время подсоединен к источнику напряжения U, а пластина жестко скреплена с положительной обкладкой. Обкладки конденсатора и пластина – квадрат с ребром а, и начальное расстояние между обкладками d << a.

172 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

ε ε2a2 U 2

Ответ: A = ( 0 ) .

ε +1 d 2

5.4.8. Между обкладками плоского воздушного конденсатора расположена диэлектрическая пластина толщиной d2 с диэлектрической проницаемостью ε, суммарная толщина оставшихся воздушных зазоров между пластиной и обкладками равна d1. Разность потенциалов между обкладками равна V. Определить силу притяжения между обкладками. Площадь всех пластин равна S.

5.4.9. Обкладки плоского воздушного конденсатора имеют площадь S и отделены друг от друга на расстояние d1. Между ними находится металлическая пластина такой же площади и толщиной d2 , изолированная от земли. Конденсатор заряжен до напряжения V и отсоединен от источника. Какую работу необходимо совершить, чтобы удалить пластину из конденсатора?

5.4.10. Два одинаковых воздушных конденсатора ёмкостью С заряжены до разности потенциалов U и отсоединены от батареи. Один из них в заряженном состоянии погружают в диэлектрик с проницаемостью ε, после чего конденсаторы соединяют параллельно. Определить энергию происходящего при этом разряда.

5.4.11. Определить высоту подъёма жидкости в расположенном вертикально плоском конденсаторе, если он подсоединен к батарее с напряжением U, расстояние между пластинами d, плотность жидкости ρ, диэлектрическая проницаемость ε.

5.4.12. Две коаксиальные трубки радиуса a и b погружаются вертикально в масляную ванну. Плотность масла ρ, диэлектрическая проницаемость ε. Разность потенциалов между трубками U. Найти высоту подъема масла в пространстве между трубками. Капиллярными силами пренебречь. Капиллярными явлениями и краевыми эффектами пренебречь.

a

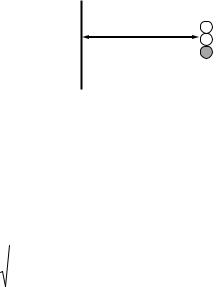
5.4.13. Некая молекула (рис. 5.11) содержит три заряда +q, +q, – 2q, которые расположены линейно на равных расстояниях a друг от

5.4.14. Незаряженный проводящий шар, плотность которого ρ1, плавает в жидкости, имеющей плотность ρ2 (ρ2 > 2ρ1) и диэлектрическую проницаемость ε. Какой заряд следует сообщить шару, чтобы он погрузился в жидкость ровно на половину? Радиус шара равен R.

Литература к главе 5

1.Матвеев А.Н. Электричество и магнетизм. §18, 19. –М.: Высшая школа, 1983.

2.Сивухин Д.В. Общий курс физики. Электричество. §28-30, §32-34, М., Физматлит, 2006..

3.Калашников С.Г. Электричество. §31-37, М.: Физматлит, 2003.

4.Тамм И.Е. Основы теории электричества. §30-34, –М.: Наука, 2003.

174 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Глава 6

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

§6.1. Теоретический материал

Электрический ток – упорядоченное движение заряженных частиц. Ток может существовать в проводящих средах и в вакууме.

Проводники – материальные тела, в которых при наличии внешнего электрического поля возникает электрический ток свободных зарядов. Если через проводник протекает электрический ток, то (в отличие от электростатики) он не является эквипотенциальной областью.

Ток в проводящей среде

Объемная плотность тока – вектор средней плотности потока зарядов, который численно равен заряду, проходящему за 1 секунду через единичную площадку, перпендикулярную скорости зарядов

j = ρv .

Размерность плотности тока [j] = А/м2. Вектор j сонаправлен с вектором скорости v упорядоченного движения положительно заряженных частиц. Здесь ρ – объёмная плотность зарядов в данной точке проводника. Если в проводнике существуют свободные заряды разных знаков с объемной плотностью ρ+ и ρ–, движущиеся со средними скоростями v+ и v – соответственно, то

где ρ – объемная плотность зарядов в проводнике, j – плотность тока. Если ток постоянный, то величина заряда в любой части объема проводника неизменна и везде выполняется соотношение:

Поверхностная плотность тока – вектор, определяемый соот-

ношением

i = σv ,

где σ – поверхностная плотность зарядов, v – вектор их средней скорости упорядоченного движения по поверхности. Размерность поверхностной плотности тока [i] = А/м.

Здесь Е – напряженность электростатического поля в проводнике, λ – удельная электрическая проводимость вещества. В системе СИ удельная электрическая проводимость измеряется в (Ом м)-1.

Если, помимо электростатического поля, на носители заряда действуют иные (так называемые, сторонние) силы, то

где Е* – напряженность поля сторонних сил, численно равная сторонней силе, действующей на свободный носитель единичного положительного заряда. Сторонние силы могут быть обусловлены, например, вихревым электрическим полем, силой Лоренца, физической или химической неоднородностью проводников, их ускоренным движением.

В однородном проводнике (λ = const) из (6.2, 6.3) следует div E = 0 и, поскольку для стационарных полей rot E = 0, поле Е

потенциально и потенциал ϕ удовлетворяет уравнению Лапласа2 ϕ= 0.

Сила тока I – скалярная величина, численно равная заряду, проходящему через поперечное сечение проводника S за единицу времени

Единица измерения силы тока Ампер [А] в системе единиц СИ является основной электромагнитной единицей.

Закон Ома для участка цепи. Сила тока, протекающего по проводнику при отсутствии в нем сторонних сил, пропорциональна напряжению U между концами проводника:

Величина R называется электрическим сопротивлением проводника. Единица измерения в системе СИ – [Ом].

(2)

E = ∫E*dl ,

(1)

величина, численно равная работе сторонних сил по переносу единичного положительного заряда по данному участку. Величина IR называется напряжением (падением напряжения) на резисторе R.

Знак ЭДС:

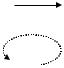
Считается, что E > 0, если сторонние силы направлены по направлению тока (например, на рис. 6.1 – при прохождении локального источника ЭДС от контакта (–) к (+)).

E < 0 в обратном случае (прохождение источника ЭДС от (+) к (–)). Мощность источника ЭДС (мощность сторонних сил):

элементах цепи. Далее производится обход контура.

Правила знаков в законе Ома для полной цепи:

Для тока: ток считается положительным (+I), если обход контура производится в направлении, совпадающем с выбранным направлением тока, и отрицательным (–I) в обратном случае;

Для ЭДС: ЭДС положительна (+E), если при обходе контура источник ЭДС проходится в направлении действия сторонних сил, и отрицательна (–E) в обратном случае.

178 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Полное сопротивление контура находится согласно правилу сложения сопротивлений при последовательном включении резисторов

RΣ = ∑Ri .

i

Если отдельные участки цепи содержат параллельно соединенные резисторы, то их эквивалентное сопротивление определяется соотношением

1 = ∑ 1 .

RΣ i Ri

Направление обхода контура можно взять любым: изменение направления обхода приведет лишь к одновременной смене знаков всех слагаемых, что не изменит уравнение по существу. Для приведенного на рис. 6.2 примера, в соответствии с выбранным направлением тока (сплошная стрелка) и выбранным направлением обхода контура (пунктирная линия со стрелкой), уравнение закона Ома для полной цепи (6.12) имеет вид

– I(R1 + R2 + R3) = –E1 + E2,

Разветвленная цепь квазилинейных проводников

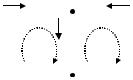
В разветвлённой цепи квазилинейных проводников существуют точки, называемые узлами цепи, в которых соединяются три или более проводника (рис. 6.3.). Такую цепь можно условно разделить на несколько замкнутых неразветвлённых контуров.

Правила Кирхгофа

Правило I. Для каждого узла цепи алгебраическая сумма сил токов равна нулю (следствие закона сохранения заряда)

При суммировании знак входящего в узел тока (обычно "+") принимается противоположным знаку выходящего ("–").

Правило II. При обходе любого замкнутого контура, выбранного в разветвленной цепи, алгебраическая сумма напряжений на сопротивлениях цепи IiRi равна алгебраической сумме ЭДС, входя-

щих в данный контур (следствие потенциальности поля, создающего постоянный ток):

Для использования данных формул сначала нужно выбрать направления токов в каждой ветви цепи, что можно сделать произвольным образом (истинные направления токов определятся потом знаками полученных решений).

зан на рис. 6.3. Произвольно выбранные направления токов показаны сплошными стрелками, направления обхода – пунктирными линиями со стрелками).

Для данного случая уравнения Кирхгофа (6.13), (6.14) будут иметь следующий вид:

Решая эту систему уравнений, получим ответ:

При составлении уравнений Кирхгофа надо иметь в виду следующее.

Полное число независимых уравнений типа (6.13) и (6.14) равняется числу неизвестных токов N. Общее же число уравнений, которые можно составить, больше числа неизвестных, поскольку часть уравнений не являются независимыми.

1) При наличии в разветвленной цепи m узлов существует только m – 1 независимых уравнений типа (6.13) для токов.

180ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

2)Новые независимые уравнения типа (6.14) можно получить только для тех контуров, которые не образуются наложением уже

ранее рассмотренных. Общее число независимых уравнений типа (6.14) будет N − m +1. Если схему можно представить на плоскости без пересечений проводников, то число таких независимых уравнений равно числу пространственных областей, на которые проводники разбивают схему. Например, на схеме рис. 6.3 таких областей две и имеется два независимых уравнения для двух показанных контуров обхода. Третье уравнение, которое можно получить обходом большого контура по периметру схемы, будет суммой или разностью этих двух уравнений, т.е. не будет независимым.

Метод контурных токов. Удобным вариантом применения правил Кирхгофа является метод контурных токов. В нем каждому выделенному в схеме контуру сопоставляется один контурный ток, одинаковый по всему контуру. Уравнения Кирхгофа (6.14) сохраняют свой вид, но теперь напряжение на каждом участке Ri, входящем одновременно в несколько (m) контуров, определяется полным током Ii через этот участок, который выражается через алгебраическую сумму контурных токов, проходящих через этот участок:

С введением контурных токов уравнения для узлов (6.13) удовлетворяются автоматически, и они становятся не нужны, в чем и состоит удобство метода при расчете цепей с большим числом узлов. Правила знаков при этом остаются прежними.

Для схемы, показанной на рис. 6.3, метод контурных токов дает следующие два уравнения (в соответствии с выбранным направлением тока и направлением обхода контуров)

Здесь учтено, что через участок R3 текут контурные токи обоих контуров. Разумеется, эта система уравнений эквивалентна системе, приведенной выше для этой же схемы.