с инета для метод

зарядов в произвольной точке границы, а также полный связанный заряд на поверхности диэлектрика.

Решение

Для ответа на первый вопрос используем непрерывность нормальной компоненты вектора индукции Dn (4.13) на границе раздела вакуум (среда 1) –диэлектрик (среда 2).

Рассмотрим напряженность поля в бесконечно малой окрестности произвольной точки А, лежащей на границе раздела (рис. 4.4). Ввиду цилиндрической симметрии системы достаточно задать лишь радиус x, на котором точка А находится от основания перпендикуляра О, опущенного из точки нахождения заряда на плоскую границу диэлектрика.

Пусть σ′(х) – плотность связанного заряда в точке А. Вблизи точки А напряженность поля будет

мерно. Нужная нам нормальная компонента поля (поле E′ (x) на рис.4.4) создается только поверхностными зарядами в непосредст-

σ′

венной окрестности точки А и имеет величину E′(x) = 2ε0 . Поле от

всех остальных связанных зарядов плоскости в этой точке направлено горизонтально вдоль плоскости (E′|| на рис. 4.4).

В первой среде (в вакууме) нормальная компонента вектора индукции, в соответствии с выбранным направлением нормали, равна согласно (4.6)

122 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Во второй среде (в диэлектрике)

Здесь учтено, что знак нормальных компонент поля E′ (x) по обе стороны границы противоположен. Из условия D1n = D2n находим:

Для вычисления величины полного связанного заряда q′ выделяем на плоскости кольцевую область с центром в точке О, расположенную между окружностями радиусов x и x + dx. Площадь этой области dS = 2πxdx, на ней находится заряд dq′ = σ′dS. Полный заряд q′ найдем, интегрируя это выражение по х от нуля до бесконечности:

Замечание. Рассмотрим случай, когда заряд q находится на границе. При h → 0 из полученного результата видно, что σ′ → 0 во всех точках, кроме х = 0. Действительно, при этом в произвольной точке А(х) нормальная компонента вектора напряженности Eq обращается в нуль, ввиду чего условие непрерывности нормальной

компоненты вектора D приводит к соотношению σ′ = −ε σ′ , кото- 2 2

рое может выполняться только при σ′ = 0. Итак, если точечный заряд q находится на плоской границе раздела вакуума и безграничного диэлектрика, то σ′ = 0 везде, кроме точки х = 0.

Величина q′ не зависит от h. Однако при h → 0 весь этот заряд собирается около точки х = 0. Поэтому напряженность поля можно вычислить как суперпозицию полей двух точечных зарядов q и q′, расположенных в одной точке х = 0. Поскольку других зарядов нет, создаваемое ими во всем пространстве поле изотропно, то есть в диэлектрике оно такое же, как в вакууме:

Это означает, что силовые линии вектора E расходятся из центра равномерно, а эквипотенциальные поверхности являются сферами.

Поле вектора D легко получить из найденной формулы:

Картина линий вектора индукции D, в отличие от картины поля E, несимметрична. Поскольку D2 > D1, силовые линии индукции, расходясь радиально от центра, имеют большую густоту в диэлектрике, чем в вакууме.

Задачи типа 4.2

Определение напряженности поля Е, потенциала φ и вектора

индукции D в системах с однородными диэлектриками

Методы решения. Использование известного или ранее рассчитанного распределения связанных зарядов и вектора поляризации. Использование граничных условий (4.11) – (4.14) и формул (4.6) – (4.9).

Задача 4.3.6 (базовая задача). Бесконечно большая пластина из однородного диэлектрика с проницаемостью ε заряжена равномерно сторонним зарядом с объемной плотностью ρ. Толщина пластины 2d. Найти напряженность электрического поля и потенциал, создаваемые этой системой, а также объемную и поверхностную плотности связанного заряда.

Решение

Из симметрии системы следует, что напряженность и потенциал зависят только от одной координаты, выбранной в направлении нормали к слою. Пусть это будет ось х декартовой системы координат с началом в центре слоя. Напряженность поля такой системы при ε = 1 была вычислена в задаче 1.3.11 (глава 1) на основе теоремы Гаусса:

Поле в пространстве между пластинами однородное, поэтому искомая разность потенциалов равна

Δφ = E1(h – d) + E2d.

Подставляя численные значения всех величин, находим приближенно: E1 = 170 кВ/м, E2 = 85 кВ/м, Δφ = 1,3 кВ. Величины напряженности существенно меньше диэлектрической прочности воздуха, которая приблизительно равна 30 кВ/см.

Δφ = = E1(h – d) + E2d = 1,3 кВ.

Дополнение. Определим силу, действующую на каждую пластину. Из определения напряженности следует, что силу можно рассчитать, если известен заряд, на который действует сила, и напряженность этого действующего поля. В нашем случае заряд первой пластины равен q1 = σ1S, где S – площадь пластин. На этот заряд действует поле, создаваемое второй пластиной. Напряженность

этого поля равна E = σ2 . В итоге находим: 2ε0

F = σ1σ2 S . 2ε0

Из численных данных можно найти лишь плотность действующей силы, т.е. силу, приходящуюся на единицу площади (электрическое давление). Она равна f = F/S = 0,5 Па.

Задачи типа 4.3

Определение емкости конденсаторов, заполненных неоднородным диэлектриком

Методы решения:

1) использование эквивалентных схем, которые представляют неоднородно заполненный диэлектриком конденсатор как систему соединенных между собой конденсаторов, заполненных диэлектриком однородно. После этого применяются формулы сложения емкостей конденсаторов при последовательном и параллельном их соединении (см.§3.1. главы 3).

Задача 4.3.10. Пространство между пластинами плоского конденсатора заполнено диэлектриком, проницаемость которого меняется по линейному закону от значения ε1 у одной пластины до значения ε2 (ε2 < ε1) у другой. Расстояние между пластинами d, площадь каждой пластины равна S. Найти емкость С конденсатора.

Решение

Способ 1. Учитывая симметрию системы, направим ось х декартовой системы координат по нормали к плоскости пластин конденсатора, а начало отсчета 0 выберем в точке пересечения оси х с пластиной, около которой проницаемость диэлектрика наименьшая (см. рис.4.9).

конденсаторов суммируются величины, обратные емкости, что для

130 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Способ 2. Пусть на обкладках конденсатора находятся заряды ±q и поверхностная плотность заряда σ = ±q/S. Тогда D = σ, и далее получаем

Ответ: C = ε0 (ε1 − ε2 )S . d ln(ε1 /ε2 )

Задача 4.3.11 (базовая задача). Первоначально в плоском воздушном конденсаторе, заряженном и отсоединенном от источника ЭДС, напряженность поля равна Е0. Затем половину пространства между пластинами конденсатора заполняют однородным диэлектриком с проницаемостью ε так, что плоская граница диэлектрика параллельна пластинам конденсатора (рис. 4.10а).

а) Найти модули векторов E и D внутри и вне диэлектрика.

б) Ответить на те же вопросы, если диэлектрик занимает все расстояние между пластинами в половине объема конденсатора (рис. 4.10б).

Решение

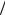В случае а) из результатов задачи 4.3.2 следует, что напряженность поля в воздушном промежутке E1 = E0 = σε0 не изменится, а в диэлектрике станет меньше в ε раз за счет поля появившихся связанных зарядов E2 = E0 ε .

Распределение сторонних зарядов на обкладках конденсатора не изменилось, поэтому не изменятся и силовые линии вектора индукции D. Из условия непрерывности Dn на границе диэлектрика заключаем, что в любой точке внутри конденсатора D1 = D2 = ε0Е0.