с инета для метод

где dq(r′) = ρ(r′)dV′, σ(r′)dS′ или τ(r′)dl′ соответственно для каждого из указанных случаев.

Электрический диполь – система двух разноименных по знаку и одинаковых по величине точечных зарядов, находящихся на небольшом расстоянии один от другого. Вектор l, проведенный от отрицательного заряда к положительному, называется плечом диполя. Вектор

p = ql

называется электрическим моментом диполя.

Напряженность поля, создаваемого диполем в точке, заданной радиус-вектором r, проведенным от центра диполя, (при условии l << r) приблизительно равна

В пределе l → 0 приведенная формула становится асимптоти- r

чески точной, а диполь называется точечным.

Электрическим дипольным моментом системы N зарядов

называется вектор

i=1

где ri – радиус-вектор i-ого заряда.

Если полный заряд системы равен нулю (электрически нейтральная система), то величина дипольного момента не зависит от выбора начала системы отсчета, поэтому радиус-векторы ri можно отсчитывать от любой точки. В таком случае на больших расстояниях от системы (намного больших ее собственных размеров), ее электрическое поле совпадает с полем точечного диполя (1.4).

Для непрерывного распределения заряда дипольный момент системы определяется интегралом

верхность пропорционален суммарному заряду, находящемуся внутри объема, ограниченного этой поверхностью

Поверхность S часто называют поверхностью Гаусса.

Электростатическая теорема Гаусса в дифференциальной форме (дифференциальная формулировка закона Кулона)

Градиент скалярной функции φ – вектор, проекции которого на оси декартовой системы координат равны частным производным функции φ по соответствующим координатам:

Сила, действующая на точечный диполь в электростатическом поле

Момент сил, действующих на точечный диполь в электрическом поле

§1.2. Основные типы задач (классификация)

1.1.Определение напряженности электрического поля заданного распределения точечных зарядов.

1.2.Определение напряженности электростатического поля, созданного зарядами, распределенными равномерно в произвольных конечных областях пространства с постоянными значениями линейной плотности заряда (τ), поверхностной плотности заряда

(σ)или объёмной плотности заряда (ρ).

Обычно в задачах этого типа заряд равномерно распределен по конечным отрезкам нитей, кольцам, участкам цилиндрических и сферических поверхностей.

1.3. Определение напряженности электростатического поля от зарядов, распределение которых имеет плоскую, осевую (цилиндрическую) или центральную (сферическую) симметрию.

Задачи этого типа легко решаются с помощью теоремы Гаусса. К ним относятся случаи, когда заряды распределены по бесконечным нитям с постоянной линейной плотностью τi, бесконечным плоскостям с постоянной поверхностной плотностью σi или же симметрично распределены по слоям, бесконечным цилиндрам или цилиндрическим слоям, а также по сферам, шарам и шаровым слоям.

1.4.Определение напряженности поля непрерывного неравномерного распределения заряда, когда плотность распределения заряда выражается какой либо функцией координат.

1.5.Определение напряженности поля, в создании которого участвуют электрические диполи.

1.6.Решение обратной задачи электростатики: по заданному значению напряженности электрического поля определить распределение зарядов, породившее это поле.

§1.3. Методы решения и примеры решения задач

Сначала сформулируем некоторые рекомендации, общие для всех задач рассматриваемого раздела.

Первый шаг в решении задачи: из анализа условий, определить к какому типу относится данная задача. Далее в зависимости от результатов анализа использовать методы решения, применяемые для данного типа задач. Чтобы яснее представить себе изучаемую систему, следует выбрать наиболее удобную систему координат и изобразить эту систему схематически на рисунке, где отметить все характерные особенности системы. Необходимо проанализировать свойства симметрии, которыми обладает изучаемая система.

Если постановка задачи ясна, то следует составить план подхода к решению. Поиск решения должен быть не хаотическим, а целенаправленным. Начинать надо с обдумывания вопроса, поставленного в задаче. Возвращаясь к теоретическому материалу, следует определить, какие теоретические положения и формулы могут помочь начать решение или сразу ответить на вопрос задачи. Не надо бояться вводить в процессе решения величины, не заданные в условии задачи. Если с помощью этих дополнительно введенных величин усматривается план доведения решения до ответа, то далее следует поступить с введенными величинами так же, как с исходным вопросом; в конце решения все использованные промежуточные величины должны быть выражены через заданные в условии

Задачи типа 1.2

Определение напряженности электростатического поля, созданного электрическими зарядами, распределенными равномерно в конечных областях пространства с постоянными значениями линейной плотности заряда (τ), поверхностной плотности заряда (σ) или объёмной плотности заряда (ρ).

Метод решения: в непрерывно распределенных зарядах выделяем физически бесконечно малые заряды – т.е. заряды, находящиеся на отрезке бесконечно малой длины dl (в случае линейного распределения), на бесконечно малой площади dS (в случае поверхностного распределения) и в бесконечно малом объеме dV (в случае объемного распределения). Эти выделенные заряды далее рассматриваются как точечные. Создаваемая ими напряженность

поля в интересующей нас точке вычисляется по формуле напряженности поля точечного заряда (1.3), после чего по принципу суперпозиции суммируются все вклады от таких зарядов. Фактически задача сводится к вычислению линейных, поверхностных или объемных интегралов. В курсе общей физики объекты выбираются обычно такими, чтобы вычисление интегралов не представляло значительных математических затруднений.

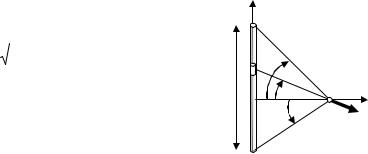
Задача 1.3.3 (базовая задача). Прямая нить длиной L заряжена равномерно с линейной плотностью τ. Найти напряженность поля в произвольной точке, расположенной на расстоянии h от нити.

Решение

Поместим начало системы координат О в основание перпендикуляра, опущенного из точки наблюдения А на направление нити, ось Y направим вдоль нити, а ось X перпендикулярно к ней (рис. 1.4, для наглядности нить представлена в виде тонкого цилиндра). Выделим на нити на произвольном расстоянии y от начала координат участок бесконечно малой длины dy, заряд которого рассматриваем как точечный. Этот заряд создает в точке А поле напряженностью

Полное значение проекций напряженности поля получим, суммируя все такие бесконечно малые вклады, т.е. вычисляя интеграл вдоль всей нити. Интегрирование выполняется совсем

просто, если в качестве переменной вместо y использовать угол α. Из соотношения y = h tg α находим

h

dy = cos2 α dα и

Пределы интегрирования определяются углами α1 и α2, под которыми из точки наблюдения A видны концы нити (оба угла считаем положительными). Итак,

Эти формулы очень удобны для анализа частных случаев. Например, если нить бесконечная, то α1 = α2 = π2 и мы получаем

далее. Конечно, эти результаты можно выразить и через координату

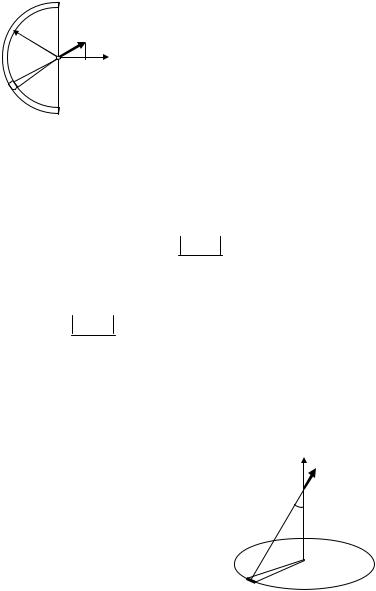
Задача 1.3.4. На одной половине тонкого кольца радиуса R равномерно распределен положительный заряд с линейной плотностью τ1, а на другой половине – заряд того же знака с плотностью τ2. Найти напряженность поля в центре кольца.

Решение

Согласно принципу суперпозиции напряженность поля в центре кольца будет равна сумме напряженностей, создаваемых каждым зарядом. Выделим на первом полукольце бесконечно малый участок dl = Rdα, несущий заряд dq = τ1 dl (рис. 1.5). Заряд dq считаем точечным, и создаваемое им в центре кольца – точке О – поле dE находим по формуле (1.3):