с инета для метод

б) Начальную емкость конденсатора можно найти из решения задачи 4.3.9, где найдена емкость плоского конденсатора, заполненного двумя слоями диэлектрика (слой толщиной d1 с проницаемостью ε1 и слой толщиной d2 = d –d1 c проницаемостью ε2):

В условиях нашей задачи, следует положить ε1 = 1, ε2 = ε и d1 = (1 – η)d, d2 = ηd. Тогда начальную емкость конденсатора можно записать как

где Q = C1U. Подставляя найденное выражение для C1, находим:

ε(ε −1)ηCU 2

A = W = 2(ε(1− η) + η)2 = 0,8мДж .

Работа против электрических сил полностью пошла на увеличение энергии конденсатора.

ηCU 2

Ответ: а) A = 2(1− η)2 =1,5 мДж ;

ε(ε −1)ηCU2

б) A = 2(ε(1− η) + η)2 = 0,8 мДж .

Задача 5.3.12. Внутри плоского конденсатора с площадью пластин S = 200 см2 и расстоянием между ними d = 0,1 см находится пластина из стекла (ε = 5), целиком заполняющая пространство между пластинами конденсатора. Какую механическую работу надо

162 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

затратить на удаление пластины, если конденсатор все время присоединен к батарее с ЭДС, равной U = 300 В?

Решение

Если в процессе удаления пластины источник ЭДС остается подключенным к конденсатору, то для расчета запасенной в кон-

денсаторе энергии следует воспользоваться формулой W = CU 2 . В 2

условиях данной задачи емкость конденсатора уменьшается; следовательно, и его энергия будет уменьшаться. Изменение энергии конденсатора равно

W = (1− ε)CU 2 < 0 . 2

Заряд на обкладках конденсатора не остается постоянным – часть заряда перемещается через источник ЭДС, увеличивая его потенциальную энергию. Элементарная работа, совершаемая против ЭДС батареи, равна dA = Udq. Если изменения происходят квазистатически, то по окончании процесса полная работа будет равна

A = U q,

где q = (ε – 1)CU – полное изменение величины заряда на обкладках. Согласно закону сохранения энергии механическая работа, совершаемая при удалении стеклянной пластины, равна

A1 = A+ W = (ε −1)CU 2 . 2

Подставляя значения параметров, получаем численный ответ:

A1 = 3,2·10-5 Дж.

Ответ: A1 = (ε −1)CU 2 = 3,2·10-5 Дж. 2

Задача 5.3.13. Конденсатор емкости C1 = 1 мкФ, предварительно заряженный до напряжения U = 300 В и отсоединенный от источника ЭДС, подключили параллельно к незаряженному конденсатору емкости C2 = 2 мкФ. Найти изменение электрической энергии этой системы к моменту установления равновесия.

Решение

При соединении конденсаторов первоначальный заряд q = C1U перераспределится так, чтобы напряжение U1 на двух конденсато-

рах стало одинаковым. Электрические силы совершат работу по перемещению зарядов и, следовательно, потенциальная энергия системы уменьшится.

Замечание. Вся потерянная системой энергия перешла главным образом в тепло за счет омического сопротивления схемы. При малом омическом сопротивлении и достаточно большой индуктивности системы будут наблюдаться затухающие колебания величины заряда на конденсаторах вплоть до достижения равновесного состояния, когда вся избыточная энергия перейдет в тепло и электромагнитное излучение.

Задача 5.3.14. Незаряженный металлический шар радиуса R помещен в однородное внешнее поле, напряженность которого равна E0. Какую работу необходимо совершить, чтобы переместить этот шар в область, где поле практически отсутствует?

Решение

Если проводящий шар находится во внешнем однородном электрическом поле E0, то явление электростатической индукции приведет к тому, что на его поверхности появятся поверхностные заряды (рис. 5.4), которые обеспечивают равенство нулю напряженности поля внутри шара. Эти заряды можно представить себе как результат малого сдвига на вектор d вдоль направления поля друг относительно друга двух равномерно заряженных по объему шаров того же радиуса R, несущих заряды противоположных зна-

166 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Задача 5.3.16. Обкладки плоского конденсатора имеют форму квадрата со стороной a и соединены с источником напряжения. Расстояние и разность потенциалов между обкладками соответственно равны d и U. В пространство между обкладками частично вдвинута пластина толщиной в форме квадрата со стороной a. Ее поверхности и стороны параллельны поверхностям и сторонам обкладок, а диэлектрическая проницаемость равна ε. Найти силу, с которой пластина втягивается в пространство между обкладками конденсатора.

Решение

При постоянном напряжении на конденсаторе его потенциальная энергия W = CU 22 изменяется только с изменением его емко-

координаты х конца вдвинутой пластины и действующую на пластину силу можно рассчитать по формуле (5.8):

Конденсатор с вдвинутой пластиной можно рассматривать как два соединенных параллельно конденсатора – воздушный, площади S1 = ax и частично заполненный диэлектриком, площадь которого S2 = a(a – x). Его емкость согласно правилу сложения емкостей равна С = С1 + С2, где

Вычисляя производную dC , находим проекцию на ось х дей- dx

ствующей на диэлектрическую пластину силы:

Знак минус соответствует силе притяжения.

Задача 5.3.17 (базовая задача). Плоский конденсатор расположен горизонтально так, что одна его пластина находится над поверхностью жидкости, другая – под ее поверхностью. Диэлектрическая проницаемость жидкости ε, ее плотность ρ. На какую высоту поднимется уровень жидкости в конденсаторе после сообщения его пластинам заряда с поверхностной плотностью σ?

Решение

На поверхность жидкости в конденсаторе будет действовать направленная вверх сила, поверхностная плотность которой определена формулой (5.12):

f = (ε −1) D2 . 2εε0 n

При равновесии эта сила скомпенсирована гидростатическим давлением:

f = ρgh.

Поскольку в нашем случае D = Dn = σ, находим ответ:

h = σ2 (ε −1) . 2εε0ρg

σ2 (ε −1)

Ответ: h = 2εε0ρg .

Замечание. Подъём жидкости реально связан с объемными силами, возникающими в области неоднородности поля у края конденсатора, хотя в приведенном энергетическом расчете краевые эффекты явно не фигурируют.

168 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Задача 5.3.18. Коэффициент поверхностного натяжения сферического мыльного пузыря λ = 0,05 Н/м, его радиус R = 1 см, наружное атмосферное давление р = 105 Па. Какой заряд q надо изотермически сообщить пузырю, чтобы его радиус увеличился вдвое?

Решение

При равновесии незаряженного мыльного пузыря радиуса R давление в его внутренней области р1 уравновешивает наружное атмосферное давление р и давление за счет поверхностного натя-

жения 4λ (здесь учтено, что мыльная пленка имеет две поверхно-

Давление газа внутри пузыря при постоянной температуре об-

ратно пропорционально объему, т.е. p1 = a , где а – коэффициент

R3

пропорциональности. Если пузырю сообщается заряд q, то к внутреннему давлению добавляется давление электростатических сил р2. Тогда условие равновесия принимает вид:

где p1′ = p1R3 r3 (r – увеличившийся радиус пузыря). Рассчитаем величину р2. Для этого выделим на поверхности пузыря малую площадку dS и определим действующую на нее силу. Поверхност-

q

ная плотность заряда на пузыре равна σ = 4πr2 .

Известно (глава 1, задача 1.3.19), что напряженность поля, созданного у поверхности сферы всеми ее зарядами, кроме заряда

σ

dq = σdS, находящегося на элементе dS, равна E = 2ε0 , поэтому на заряд dq будет действовать сила

dF = Edq = σEdS ,

и эта сила будет создавать давление

Решая систему уравнений (5.17) – (5.18) с учетом условия r = 2R, находим ответ:

q2 = (64πε0R3 )(12λ + 7 pR) .

Если R >> λ/р = 5 10-5 см (как и определено условиями задачи),

то

q = 8πR2 7ε0 p = 6,2 10−6 Кл . Ответ: q = 8πR2 7ε0 p = 6,2 10−6 Кл .

Задача 5.3.19. Конденсатор переменной емкости состоит из двух неподвижных металлических пластин, расположенных на расстоянии d друг от друга, и подвижной диэлектрической пластины, которая может поворачиваться и входить в зазор между металлическими пластинами (рис. 5.7). Все пластины имеют форму полукруга радиуса R, причем зазоры между диэлектрической пластиной и пластинами конденсатора пренебрежимо малы по сравнению с d. Пренебрегая краевыми эффектами, найти момент сил М, действующих на диэлектрическую пластину, когда она выведена из положения равновесия. Конденсатор поддерживается при разности потенциа-

лов V, диэлектрическая проницаемость подвижной пластины равна ε.

положения равновесия на угол θ диэлектрической пластиной можно заменить эквивалентной схемой двух включенных параллельно

конденсаторов, у одного из которых площадь пластин S1 = R2θ2 и между пластинами находится воздух, а у другого площадь пластин

S2 = R2( π − θ )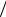2 и между пластинами находится диэлектрик ε. Емкость такого конденсатора равна

C = C1 + C2 = ε0 (S1 + εS2 ) . d

Для определения момента силы М применим формулу (5.9), записав энергию конденсатора в виде W = CV 22. Выполняя диффе-

ренцирование, получаем ответ: M = ε0 (ε −1)R2V 2 . 4d