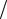Гл. 9. Энергия и силы в магнитостатике |
281 |
Действие магнитной составляющей си- |
|
|
|
|
|
|
|
|
лы Лоренца F приводит к тому, что при |
|
|
|
|
включении тока электроны начинают сме- |
|
|
|
|
щаться к оси проводника (рис. 9.4). В ре- |
|
|
|
|
зультате на поверхности появляется избы- |
|
|
|
|
точный положительный заряд, а в остальном |
|
|
|
|
|
|
F |
|
объеме – отрицательный. Таким образом, |
|
|
|
|
|
|
|
возникает электрическое поле, со стороны |
|
|
|
|
|
|
B |
|
которого на электроны также действует си- |
|
|
|
|
|
|
|
ла. Равновесие в проводнике будет достиг- |
|
|
|
|
нуто тогда, когда действующая на электроны |
|
|
|
|
сила Лоренца (9.12) станет равной нулю, и в |
|
|
U |
каждой точке проводника будет выполнять- |
|
|
ся равенство |
|
|
|
|
|
|
|
|
eE = −eVB .
Индукция магнитного поля на расстоянии r от оси сплошного цилиндрического проводника равна
B = µ0I r
2πR2
Рис. 9.4. Определение разности потенциалов U между осью и поверхностью сплошного цилиндрического проводника с током (задача 9.3.5)
(см. задачу 7.3.10 главы 7). Напряженность электрического поля в произвольной точке проводника направлена по радиусу проводника и для ее проекции на радиальное направление получаем:
|
E = −VB = − |
I |
|
µ0 I |
|
r . |
|
neπR2 2πR |
2 |
|
|
|
Отсюда находим разность потенциалов между осью проводника и его поверхностью
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
µ |
I 2 |
|
|
µ |
I 2 |
|
|
U = −∫Edr = ∫ |
|
0 |
|
|
rdr = − |
|
0 |
|
|
. |
|
2 |
R |
4 |
|
2 |
R |
2 |
|
R |
|
R |
2neπ |
|
|
4neπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: U = − |
µ |
0 |
I 2 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
4neπ2R2 |
|
|
|
|
|
|
|
|
|
Замечание. Чтобы найти распределение заряда внутри провода, можно воспользоваться результатами задачи 1.3.13 главы 1. В ней было показано, что такая напряженность электрического поля, пропорциональная радиус-вектору r точки, получается внутри равно-
ρ
2ε0
282 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
мерно заряженного цилиндра и равна E = r , где ρ – плотность
заряда. Приравнивая это выражение полученной выше напряжен-
I 2
ности Е, получаем ρ = −ε0µ0 neπ2 R4 .
Задачи типа 9.2
Нахождение энергии магнитного поля и магнитных сил, действующих на проводники с током, ограниченные
в пространстве
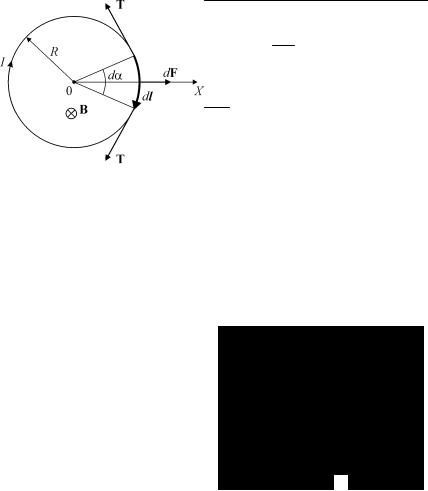
Задача 9.3.6. По тонкой проволоке диаметром D, согнутой в виде окружности радиуса R, течет постоянный ток I. Проволока разрывается, если величина механического напряжения в ней достигает величины σ0. При каком значении индукции Bк однородного магнитного поля, перпендикулярного плоскости кольца, произойдет разрыв проволоки?
Решение
Замкнутое кольцо с током можно рассматривать как магнитный момент pm = ISn (см. (7.16) в главе 7). Так как вектор индукции магнитного поля параллелен pm, то согласно (9.3) отсутствует вращающий момент, действующий на проводник со стороны внешнего магнитного поля.
А
T′
Рис. 9.5. Силы, действующие на элемент кольца с током во внешнем магнитном поле В (задача 9.3.6)
Поскольку магнитное поле однородно, то согласно (9.2), полная сила, действующая на кольцо со стороны магнитного поля, также равна нулю, т.е. проводник находится в положении равновесия.
На элемент проводника dl (рис. 9.5) действует сила Ампера (9.1)
dFA = I [dlB].
Эта сила должна быть скомпенсирована равнодействую-
Гл. 9. Энергия и силы в магнитостатике |
283 |
щейdFT сил натяжения Т и Т′, приложенных к концам данного
|
элемента dF = Tdα = T |
dl |
. Приравнивая модули этих сил, получа- |
|
|
|
T |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ем |
|
|
|
|
|
|
|
|
|
|
|
T = IBR . |
|
|
|
|
|
Проволока разорвётся, если механическое напряжение в ней |
|
|
|
|
T |
= σ |
|
(где S = |
πD2 |
|
достигнет предельного, то есть |
|
0 |
|
– площадь |
|
S |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поперечного сечения проводника).
Окончательно получим: B = σ0πD2 . 4IR
Ответ: B = σ0πD2 . 4IR
Задача 9.3.7 (базовая задача). Две катушки с магнитными моментами p1 и p2 расположены так, что их оси находятся на одной прямой. Расстояние L между ними велико по сравнению с размерами катушек. Определить силу взаимодействия между катушками.
Решение
Поскольку L намного больше размеров катушек, то такую систему можно рассматривать как систему из двух точечных магнитных моментов (см. теоретический материал главы 7), один из которых находится в поле, создаваемом другим.
Будем рассматривать вторую катушку в поле первой. Выберем ось Х декартовой системы координат совпадающей с прямой, соединяющей центры катушек (см. рис. 9.6). Ввиду симметрии задачи сила будет иметь только х- компоненту. Тогда согласно (9.2) на вторую катушку действует сила, величина которой равна
F = Fx = p2x ∂B1x .
∂
x
Согласно соотношению
(7.21) теоретического мате- |
Рис. 9.6. К расчёту силы взаимодействия |
риала главы 7, магнитное поле |
двух магнитных диполей (задача 9.3.7) |
284 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
на оси точечного магнитного момента равно B = µ0 2pm , следова- 4π x3
тельно, индукция магнитного поля, создаваемого первой катушкой
равна B |
= µ0 |
p1x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1x |
2π x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= p |
|
∂ |
µ |
0 |
|
p |
|
|
= − |
3µ |
p |
p |
2x |
|
|
|
|
|
|
|
|
|
|
|
Окончательно получим: F |
|
|
|
|
|
1x |
|
|
|
|
0 1x |
|
. |
|
|
|
|
|
|
|
|
2πL4 |
|
|
|
|
|
|
x |
|
2x ∂x 2π x3 |
x=L |
|
|
|
|
|
Ответ: F = − |
3µ0 p1 p2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πL4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Катушки притягиваются |
(Fx < 0), |
если |
p1x и |
p2х |
имеют одинаковый знак (p1 ↑↑ p2) и отталкиваются (Fx > 0), если p1x и p2х имеют разные знаки (p1 ↑↓ p2) – ситуация, приведённая на
рис. 9.6.
Задача 9.3.8 (базовая задача). По длинному однослойному соленоиду с n витками на единицу длины течет ток I. Определить давление, действующее на боковую поверхность соленоида.
|
Решение |
|
|
|
|
|
|
Каждый из витков со- |
|
|
|
|
|
|
|
|
леноида представляет со- |
|
|
|
|
бой кольцо с током, нахо- |
|
|
|
|
дящееся во внешнем од- |
|
|
|
|
нородном (если пренеб- |
|
|
|
|
речь |
краевыми |
эффекта- |
|
|
|
|
ми) магнитном поле, пер- |
|
|
|
|
пендикулярном |
его |
плос- |
|
|
|
|
кости, |
которое |
создаётся |
|
|
|
|
всеми |
остальными |
витка- |
|
|
|
|
ми |
соленоида |
(см. |
|
|
|
|
рис. 9.7). Согласно |
задаче |
Рис.9.7. Силы, действующие на виток со- |
|
9.3.6, |
пондеромоторные |
|
леноида со стороны его собственного маг- |
|
силы |
F стремятся |
увели- |
нитного поля (задача 9.3.8) |
|
чить |
радиус |
соленоида. |
|
|
|
Найдем эти силы энергетическим методом.
Пусть радиус соленоида увеличился на dR при неизменной силе тока. Тогда согласно (9.8′) работа сил давления на боковую по-
Гл. 9. Энергия и силы в магнитостатике |
285 |
верхность соленоида будет равна приращению его энергии
δA = pdV = p2πRldR = δW I=const ,
где V – объем соленоида, R – его радиус, l –длина. Энергия соленоида согласно (9.5) равна
W = 1 LI 2 = 1 µ0n2πR2 lI 2 ,
22
где использовано, что индуктивность соленоида L = µ0n2V (см. задачу 8.3.10 главы 8).
Из этих соотношений находим величину давления
p = |
1 ∂W |
|
= |
1 ∂ |
|
1 |
µ |
n2πR2l I 2 |
|
= |
µ |
n2I 2 |
∂ |
(R2 )= |
|
|
|
|
|
|
|
|
|
0 |
|
|
2πRl |
∂R |
|
|
|
|
2 |
4R ∂R |
|
I |
|
2πRl ∂R |
0 |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0n2 I 2 = B2 ,
22 0
где B = µ0nI – индукция магнитного поля на оси длинного соленоида (см. задачу 7.3.5 главы 7).
Ответ: p = µ0n2I2  2 .
2 .
Замечание 1. Длинный соленоид разделяет все пространство на две области: внутри соленоида, в которой существует магнитное поле с индукцией B = µ0nI (см. задачу 7.3.5 главы 7), и снаружи соленоида – где магнитное поле очень мало.
Согласно (9.11) давление, оказываемое на боковую поверхность соленоида силами Ампера равно
p = w − 0 = |
B2 |
= |
µ |
n2 I 2 |
|
0 |
. |
|
|
1 |
2µ0 |
|
|
2 |
|
|
|
Замечание 2. Наличие сил давления, действующих на боковую поверхность соленоида, приводит к тому, что максимальное значение индукции магнитного поля, которое можно получить с помощью соленоидов, не превышает 50 Тл (для импульсного соленоида). При такой величине B на проволоку из бериллиевой бронзы, из которой изготавливаются импульсные соленоиды, оказывается дав-
ление равное p = B2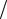 (2µ0 ) ≈ 2 109 Па , близкое к её пределу прочности.
(2µ0 ) ≈ 2 109 Па , близкое к её пределу прочности.
286 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Замечание 3. Вследствие взаимного притяжения витков соленоида на его торцевую поверхность будут действовать силы, стягивающие его. Величину давления, действующего на торцевую поверхность соленоида можно определить аналогично решению данной задачи (см. задачу 9.4.7 для самостоятельного решения).
Задачи типа 9.3
Определение вращающего момента и сил, действующих на проводник с током и магнитный диполь в магнитном поле
Задача 9.3.9 (базовая задача). Квадратная рамка со стороной
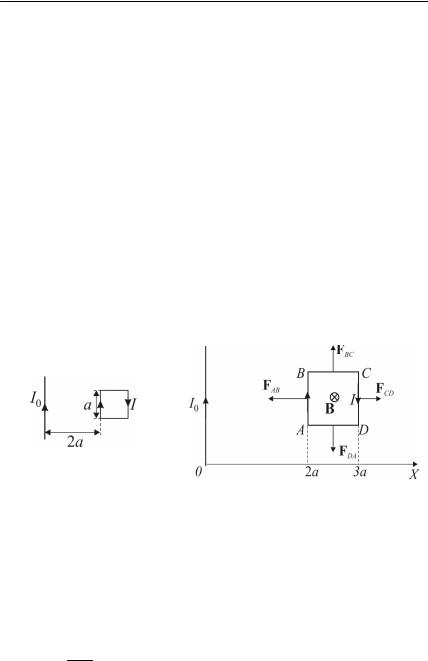
а, изготовленная из тонкого проводника, расположена в одной плоскости с длинным прямым проводом, по которому течет ток I0. Определить внешнюю силу, которая удерживает рамку в равновесии, если по ней течёт ток I, а расстояние между проводом и ближней к нему стороной рамки равно 2а (рис. 9.8 а).
Рис. 9.8 а. Взаимное располо- Рис.9.8 б. Определение силы, действующей на
жение проводников с токами в |
рамку со стороны магнитного поля прямого |
задаче 9.3.9 |
провода (задача 9.3.9) |
Решение
Способ 1. Согласно закону Ампера (9.1) на стороны рамки будут действовать разные силы со стороны магнитного поля прямого провода с током I0. Направим ось Х перпендикулярно проводу в плоскости рамки. Вектор магнитной индукции поля прямого провода В направлен перпендикулярно плоскости рамки, а его модуль
равен B = µ0I (см. задачу 7.3.9 главы 7), где I – сила тока в прово- 2πx
де, а х – расстояние от него до рассматриваемой точки.
Гл. 9. Энергия и силы в магнитостатике |
287 |
Полная сила, действующая на рамку со стороны магнитного поля, равна векторной сумме сил
F = FAB + FBC + FCD + FDA
(рис. 9.8б). Так как на участках рамки BC и DA токи текут в разные стороны, а направление магнитного поля одинаково, то FBC = – FDA и сумма этих сил равна нулю.
Определим силы, действующие на две других стороны рамки. Используя соотношение (9.1), для модуля сил имеем:
F |
= IaB |
|
|
|
= µ0I0I . |
|
|
|
AB |
|
|
|
x=2a |
4π |
|
|
|
|
|
|
|
F |
= IaB |
|
|
|
= µ0I0I . |
|
|
|
CD |
|
|
|
x=3a |
6π |
|
|
|
|
|
|
|
|
Векторы FАВ и FСD направлены противоположно и, следовательно, х-компонента результирующей силы, действующей на рамку со стороны магнитного поля, равна
Fx = − µ0I0I + µ0I0I = − µ0I0I
4π 6π 12π и направлена в сторону провода против оси Х.
Для того, чтобы рамка находилась в равновесии, к ней должна быть приложена внешняя сила F′, равная по величине и противопо-
ложная по направлению силе F, то есть Fx′ = µ0I0I . 12π
Способ 2. При постоянстве токов, текущих в проводниках, согласно соотношению (9.8′)
δA = Fdx = δW I=const .
Так как в рассматриваемой задаче токи, текущие в проводниках, не изменяются, то внешнюю силу, действующую на рамку, можно найти как
Энергия магнитного поля, созданного двумя контурами с токами, согласно (9.6) складывается из собственных магнитных энергий контуров и их взаимной энергии. Собственные магнитные энергии контуров – постоянные величины. От координаты х зависит только энергия взаимодействия, поэтому
W(x) = Wвзаим= L12 x)I0 I ,
288 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
где L12 – коэффициент взаимной индукции системы «провод – рамка».
Найдем взаимную индуктивность L12 контуров.
Магнитный поток через рамку, создаваемый полем провода, ра-
вен
|
|
|
x+a |
µ |
0 |
I |
0 |
|
|
|
µ |
|
I |
|
a |
x + a |
|
|
|
|
|
|
|
|
|
Φ = BdS = |
|
|
|
|
|
|
adx = |
|
0 |
|
0 |
|
ln |
|
= L |
|
I |
|
(см. главу 8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
∫ |
|
|
|
∫ |
|
2πx |
|
|
2π |
|
|
x |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда L = µ0a ln |
x + a |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
2π |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = |
∂ |
µ |
|
I |
|
|
Ia |
x + a |
|
= − |
µ |
|
I |
|
Ia |
a |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
ln |
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π x(x + a) |
|
|
|
∂x 2π |
|
|
x |
I=const |
|
|
|
При х = 2а |
F = − µ0I0Ia . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как получившаяся величина отрицательна, искомая магнитная сила направлена против направления оси х, что соответствует притяжению рамки к проводу.
Ответ: Fx′ = µ0I0 I . 12π
Задача 9.3.10. Соленоид радиуса R и длины l (l >> R) имеет обмотку, состоящую из N витков. По соленоиду течет ток силы I. В центре соленоида на его оси помещена небольшая катушка, имеющая магнитный момент pm, направленный перпендикулярно оси соленоида. Определить величину момента сил М, действующих на катушку.
Решение
Внутри длинного соленоида магнитное поле однородно. Вектор магнитной индукции такого поля направлен вдоль оси соленоида (см. рис. 9.9) и равен по модулю
N
B = µ0nI = µ0 l I .
Будем рассматривать катушку, как точечный магнитный диполь. Тогда в соответствии с (9.3) момент сил по модулю будет равен
Гл. 9. Энергия и силы в магнитостатике |
289 |
Рис. 9.9. К определению вращающего момента сил Ампера, действующего на магнитный диполь, помещённый на оси соленоида (задача 9.3.10)
N M = pm Bsinα = pmµ0 l I ,
где α = 90° – угол между векторами pm и В.
Ответ: M = µ0 pm NI . l
Замечание. Если внутренняя катушка ориентирована соосно соленоиду, то в соответствии с (9.4) момент сил, действующих на неё со стороны магнитного поля соленоида, равен нулю.
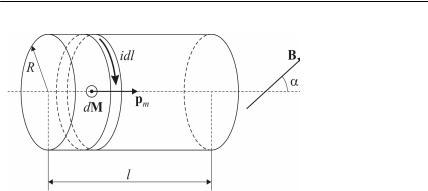
Задача 9.3.11. На круглый короткий деревянный цилиндр объёмом V в один слой намотана катушка. По катушке течет ток, поверхностная плотность которого равна i. Определить величину механического момента, который удерживает цилиндр в равновесии, если он находится во внешнем однородном магнитном поле, вектор индукции которого В образует угол α с осью цилиндра.
Решение
Рассмотрим элемент катушки длиной dl. Согласно определению (7.16) главы 7, этот элемент можно рассматривать, как магнит-
ный диполь с моментом pm = ISn = idl πR2n (где R – радиус катушки), направленным вдоль оси цилиндра (см. рис. 9.10). В соответствии с (9.4) на этот элемент катушки со стороны магнитного поля действует вращающий момент, равный по модулю
dM = pm Bsinα = idl πR2Bsinα .
290 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Рис. 9.10. Определение момента сил, действующих на элемент катушки с током во внешнем магнитном поле (задача 9.3.11
Считая, что геометрические размеры катушки (радиус R и длина l) совпадают с размерами деревянного цилиндра, на который она намотана, получим выражение для момента, действующего на всю катушку со стороны магнитного поля
ll
M = ∫dM = ∫idl πR2Bsinα = iVBsinα .
00
При интегрировании учтено, что объём катушки равен
V= lπR2 .
Вусловиях равновесия механический момент, который удерживает цилиндр с катушкой в равновесии, равен по величине моменту магнитных сил, который стремиться повернуть катушку.
Ответ: M = iVBsinα .
Задача 9.3.12. Замкнутый контур с током I, состоящий из двух полуокружностей радиусов а и b, соединённых прямыми участками (см. рис. 9.11а), находится в поле длинного прямого проводника с током I0. Плоскость контура перпендикулярна прямому проводнику, а центры полуокружностей лежат на оси прямого проводника. Найти момент сил Ампера, действующих на замкнутый контур.
Решение
Силовые линии индукции магнитного поля, создаваемого бесконечным прямым проводником с током, являются окружностями, плоскость которых перпендикулярна проводнику. На расстоянии х от проводника величина магнитной индукции его поля равна
B = µ0I0 (см. задачу 7.3.1 главы 7). Следовательно, в каждой точке 2πr