с инета для метод

ρ(x) = div D =

Полный свободный заряд в объеме конденсатора равен

Поскольку поле Е внутри неоднородно, в среде появится неоднородная поляризация P(x) = ε0(ε–1)E(x) и связанные поляризаци-

Замечание 1. Можно решить данную задачу и другим способом

– найти сопротивление конденсатора (согласно методу, предложенному в п. 6.2.1), а затем воспользоваться законами Ома и Джоуля– Ленца в интегральной форме (6.5) и (6.8).

Замечание 2. Еще проще получить результат, воспользовавшись формулой (6.7) теоретического материала RC = ρε0ε, справедливой для электродов любой формы. Действительно, (учитывая, что ε = 1

и R = ρε0 ) сразу получаем

C

Задача 6.3.8. Сферический конденсатор заполнен однородным веществом с диэлектрической проницаемостью ε и удельным сопротивлением ρ. Первоначально конденсатор не заряжен. Найти количество теплоты, выделившееся в системе, после сообщения внутренней обкладке конденсатора заряда q0. Радиусы обкладок конденсатора равны а и b = 3а.

Решение

После сообщения внутренней обкладке конденсатора заряда между его обкладками возникнет электрический ток, который будет течь до тех пор, пока разность потенциалов между внутренней и внешней обкладками не станет равной нулю. То есть в конечном состоянии весь заряд окажется распределенным по внешней обкладке конденсатора.

194 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Способ 1. Опираясь на решение задачи 6.3.3 можно рассматривать такой конденсатор как проводник сопротивлением R.

Обозначим через q1 = q заряд на внутренней сфере в произвольный момент времени, тогда заряд внешней сферы q2 = q0 – q. Разность потенциалов между ними в процессе перетекания заряда

ab

где C = 4πεε0 b − a – ёмкость сферического конденсатора (см. (3.9),

глава 3). В соответствии с законом Джоуля–Ленца для тепла dQ, выделившегося в проводнике за время dt, получим:

dQ = I2Rdt = IR Idt = U R Idt = −U dq = − q dq ,

R C

где dq = –Idt – убыль заряда внутренней обкладки за время dt.

Всё тепло, выделившееся в конденсаторе за время перетекания заряда, можно рассчитать как

q2

Ответ: Q = 0 . 12πaεε0

Замечание 1. Выделившееся тепло не зависит от сопротивления между обкладками конденсатора. Величина сопротивления влияет только на скорость процесса.

Замечание 2. Выделившееся тепло проще найти из закона сохранения энергии без расчета силы тока. Оно будет равно разности начальной и конечной электростатической энергии системы. Учи-

q2

тывая, что энергия заряженной сферы радиуса r равна 8πε0r , сразу

Задачи типа 6.3

Цепи квазилинейных проводников

Метод решения. Для неразветвленных (последовательных) цепей – применение закона Ома для полной цепи (6.12). Для разветвленных цепей – применение правил Кирхгофа в форме (6.13– 6.14) или (6.15).

Два примера решения задач типа 6.2.3 были рассмотрены выше при анализе формул (6.12–6.14).

Задача 6.3.9 (базовая задача). Найти сопротивление между точками А и В в схеме, представленной на рис. 6.8а.

Решение

Рис. 6.8 а – схема соединения резисторов в задаче 6.3.9; б – схема цепи и контурные токи

Пусть к точкам А и В, между которыми нужно определить сопротивление, подключен источник с ЭДС E (рис. 6.8б). Применим метод контурных токов. Проводники разбивают данную схему на 3 области. Каждой из них сопоставим соответствующие контурные

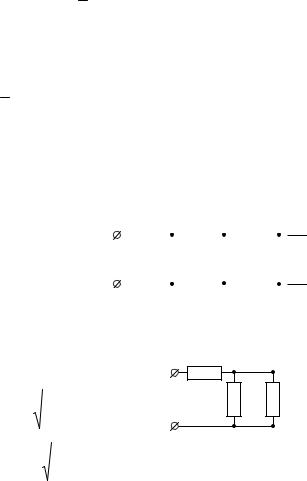
198 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

Решение

Данная задача не сводится к нераз-

водников, выходящих из А. Подсоединим теперь такой же источник ЭДС минусом к точке В, а плюсом – к бесконечно удаленному проводнику. Поскольку относительно бесконечности точка В эквивалентна А, то в точку В по каждому из 4 проводников будут сходиться токи величиной − I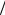4 , давая в сумме полный ток –I. Пусть будут теперь подключены оба источника ЭДС. Полный ток на бесконечно удаленный проводник обратится в нуль, т.е. ток будет течь только между точками А и В.

RAB = UAB 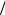IAB = R2 . Решение этой задачи по правилам Кирхгофа привело бы к бесконечной системе уравнений.

1

Ответ: RAB = 2 R .

§6.4. Задачи для самостоятельного решения

6.4.1. Два одинаковых металлических шара с радиусами a находятся в однородной среде с удельным сопротивлением ρ. Определить сопротивление R между шарами, считая, что расстояние между шарами много больше их радиуса.

ρ

Ответ: R = 2πa .

6.4.2. Найти сопротивление между внутренней и внешней поверхностями кольца толщиной d. Материал кольца имеет удельное сопротивление ρ. Радиусы внутренней и внешней частей кольца равны a и b (a < b).

Ответ: R = ρ ln b . 2πd a

6.4.3. Плоский конденсатор, заполненный веществом, диэлектрическая проницаемость которого равна ε, за время τ теряет треть сообщенного ему заряда. Считая, что утечка заряда происходит только через диэлектрическую прокладку, найти удельное сопротивление её материала.

τ

Ответ: ρ = ( ) .

εε0 ln 32

6.4.4. Обкладкам конденсатора емкости С сообщили заряды, равные соответственно +q0 и –q0. Затем обкладки замкнули через сопротивление R. Найти заряд, протекший в цепи за время τ.

Ответ: q = q0 (1− e−τRC ).

6.4.5. Зазор между обкладками плоского конденсатора толщиной d заполнен последовательно двумя диэлектрическими слоями одинаковой толщины. Удельные сопротивления слоев соответственно равны ρ1 и ρ2, диэлектрическая проницаемость ε = 1. Площадь обкладок S. На конденсатор подано напряжение U. Найти тепловую мощность, выделяемую в каждом слое.

6.4.6. Металлический шар радиуса R находится в среде с удельной проводимостью λ. На шар в некоторый момент времени помещен заряд q. Определить количество теплоты, выделившееся во всей среде за время, пока весь заряд стечет с шара.

q2

Ответ: Q= 8πε0R .