Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

821

.pdf

Скачиваний:

Добавлен:

09.01.2024

Размер:

5.5 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3113 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Второй уровень сложности

7. Составление канонического уравнения эллипса по заданной малой полуоси и эксцентриситету

Задание 7. Составить каноническое уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, что малая полуось равна и эксцентриситет равен .


											√15																			, =										√7		.
7.1. = 7, =											√15			.													7.2. = 3√2													√7
7.1. = 7, =														.													7.2. = 3√2
												8																									4
																	√19							.			7.4. = 5, =								2	.
7.3. = 2√15, =																	√19																		2
7.3. = 2√15, =																	9
																	9												3

														√10																		, =									√11						.
7.5. = 2√		3			, =									√10						.							7.6. = 2√14														√11
7.5. = 2√		3			, =															.							7.6. = 2√14
																5																									5

7.7. = 5, =											2√14						.										7.8. = 8, =								1	.
7.7. = 5, =																	.										7.8. = 8, =									.
												9																	3
7.9. = 2√					, =									√2				.																			1	.
		3												√2													7.10. = 6, =										1
		3																									7.10. = 6, =
															2																						2
7.11. = 8, =													√5		.												7.12. = 9, =										√10				.
7.11. = 8, =															.												7.12. = 9, =										8				.
												3																									8

7.13. = 4, =													√10				.										7.14. = 4, =										2√5				.
7.13. = 4, =																	.										7.14. = 4, =														.
												10																									5
													√14																												√29					.
7.15. = 5, =													√14				.										7.16. = 2√5, =														√29
7.15. = 5, =																	.										7.16. = 2√5, =														7
												4																													7

																	1		.																						√17 .
7.17. = 4√3, =																	1										7.18. = 4√2, =
7.17. = 4√3, =																											7.18. = 4√2, =
																2																									2

													√21																												√6			.
7.19. = 2, =													√21				.										7.20. = 2√3, =														√6
7.19. = 2, =																	.										7.20. = 2√3, =														3
												5																													3

													2√14																												√11						.
7.21. = 5, =													2√14							.							7.22. = 2√5, =														√11
7.21. = 5, =																				.							7.22. = 2√5, =														4
														9																											4
7.23. = 6, =													√13				.										7.24. = 10, =												3		.
7.23. = 6, =																	.										7.24. = 10, =														.
												7																									5
																	7										7.26. = 2√							, = √6 .
7.25. = 6√2, =																	7				.								10
7.25. = 6√2, =																11					.								10
																11																									4

																	√17						.																		√7			.
7.27. = 2√2, =																	√17										7.28. = 2√2, =														√7
7.27. = 2√2, =																5											7.28. = 2√2, =
																5																									3
																	√2					.															√7				.
7.29. = 2√6, =																	√2										7.30. = 9, =										√7
7.29. = 2√6, =																											7.30. = 9, =
																2																					4
													√51																												√3			.
7.31. = 7, =													√51				.										7.32. = 2√3, =														√3
7.31. = 7, =																	.										7.32. = 2√3, =
												10																													3

													√3																												√5			.
7.33. = 4, =													√3		.												7.34. = 2√5, =														√5
7.33. = 4, =															.												7.34. = 2√5, =
												3																													3
7.35. = 2√										, =										√41					.																5		.
				10																√41							7.36. = 2√6, =														5
				10																							7.36. = 2√6, =
																9																									7
8. Построение эллипса по заданному уравнению
Задание 8. Построить эллипс по заданному уравнению.
						10																									2
8.1. 1) = −						10			√49 − 2;																		2) = −2 +				2		√25 − 2															.
8.1. 1) = −									√49 − 2;																		2) = −2 +						√25 − 2															.
7																													5
	5
8.2. 1) =	5		√64 − 2;																								2) = −3 − 2√9 − 2.
8.2. 1) =			√64 − 2;																								2) = −3 − 2√9 − 2.
8																												3
8.3. 1) = 4√1 − 2;																											2) = 5 −	3	√49 − 2																.

																												7
							1																					3
8.4. 1) = −							1	√36 − 2																		;	2) = 5 +	3	√4 − 2.
8.4. 1) = −								√36 − 2																		;	2) = 5 +	2	√4 − 2.
3																												2
																											121

				4																1
8.5. 1) = −				4			√9 − 2;							2)	= −4 +					1	√36 − 2			.
8.5. 1) = −				3			√9 − 2;							2)	= −4 +						√36 − 2			.
		5		3												5		3

8.6. 1) =			√81 − 2						;					2)	= 8 −			√9 − 2.
8.6. 1) =			√81 − 2						;					2)	= 8 −			√9 − 2.
9															3
	7																			1
8.7. 1) =	7		√16 − 2;											2)	= −1 +					1	√16 − 2			.
8.7. 1) =			√16 − 2;											2)	= −1 +						√16 − 2			.
4																		2
		5														1
8.8. 1) =		5	√36 − 2						;					2)	= 3 −	1		√49 − 2.
8.8. 1) =			√36 − 2						;					2)	= 3 −			√49 − 2.
6															3					5
8.9. 1) = −5√1 − 2;														2)	= −4 −					5	√36 − 2			.
8.9. 1) = −5√1 − 2;														2)	= −4 −						√36 − 2			.
			3													5		6
8.10. 1) =			3		√49 − 2					;				2)	= 2 −	5		√4 − 2.
8.10. 1) =			7		√49 − 2					;				2)	= 2 −			√4 − 2.
			7												2
			5																	1
8.11. 1) =			5		√16 − 2;									2)	= −9 +					1	√9 − 2		.
8.11. 1) =			4		√16 − 2;									2)	= −9 +						√9 − 2		.
			4				7											3
8.12. 1) = −							7	√64 − 2				;		2)	= 3 + 3√4 − 2.
8.12. 1) = −						8		√64 − 2				;		2)	= 3 + 3√4 − 2.
							2									8
8.13. 1) = −							2	√121 − 2					;	2)	= 4 −	8		√25 − 2.
8.13. 1) = −						11		√121 − 2					;	2)	= 4 −			√25 − 2.
						11									5
							9													2
8.14. 1) = −							9	√25 − 2;						2)	= −1 −					2	√9 − 2		.
8.14. 1) = −						5		√25 − 2;						2)	= −1 −						√9 − 2		.
						5												3
			3																5
8.15. 1) =			3		√16 − 2					;				2)	= −7 +				5		√16 − 2.
8.15. 1) =			4		√16 − 2					;				2)	= −7 +						√16 − 2.
			4														4	4
8.16. 1) = 6√1 − 2;														2)	= 2 +		4	√49 − 2				.
8.16. 1) = 6√1 − 2;														2)	= 2 +			√49 − 2				.
							2								7				5
8.17. 1) = −							2	√9 − 2			;			2)	= −6 +				5		√4 − 2.
8.17. 1) = −						3		√9 − 2			;			2)	= −6 +						√4 − 2.
						3											5	2
8.18. 1) = 2√4 − 2;														2)	= 5 −		5	√49 − 2				.
8.18. 1) = 2√4 − 2;														2)	= 5 −			√49 − 2				.
			5												7				8
8.19. 1) =			5		√81 − 2					;				2)	= −2 −				8		√9 − 2.
8.19. 1) =			9		√81 − 2					;				2)	= −2 −						√9 − 2.
			9				5										3	3
8.20. 1) = −							5	√16 − 2;						2)	= 4 +		3	√64 − 2				.
8.20. 1) = −						4		√16 − 2;						2)	= 4 +			√64 − 2				.
			3			4									4				5

8.21. 1) =					√49 − 2					;				2)	= −3 −						√4 − 2.
8.21. 1) =			7		√49 − 2					;				2)	= −3 −						√4 − 2.
			7				6										1	2
8.22. 1) = −							6	√25 − 2;						2)	= 5 −		1	√16 − 2				.
8.22. 1) = −						5		√25 − 2;						2)	= 5 −			√16 − 2				.
			5			5									2				4

8.23. 1) =					√64 − 2					;				2)	= −7 −						√9 − 2.
8.23. 1) =			8		√64 − 2					;				2)	= −7 −						√9 − 2.
			8															3
			5														2
8.24. 1) =			5		√9 − 2;									2)	= 2 +		2	√36 − 2				.
8.24. 1) =			3		√9 − 2;									2)	= 2 +			√36 − 2				.
			3				5								3
8.25. 1) = −							5	√81 − 2				;		2)	= −3 − 4√1 − 2.
8.25. 1) = −						9		√81 − 2				;		2)	= −3 − 4√1 − 2.
						9											1

8.26. 1) = 3√4 − 2;														2)	= 4 −			√64 − 2				.
8.26. 1) = 3√4 − 2;														2)	= 4 −			√64 − 2				.
															4
							7								= 6 −	5
8.27. 1) = −							7	√25 − 2;						2)		5		√9 − 2.
8.27. 1) = −						5		√25 − 2;						2)				√9 − 2.
						5									3
							1								= −5 +					2
8.28. 1) = −							1	√16 − 2				;		2)						2	√36 − 2			.
8.28. 1) = −						2		√16 − 2				;		2)							√36 − 2			.
						2												3
			3																	5
8.29. 1) =			3		√16 − 2;									2)	= −3 −					5	√64 − 2			.
8.29. 1) =			2		√16 − 2;									2)	= −3 −						√64 − 2			.
			2															8
			2													9
8.30. 1) =			2		√9 − 2				;					2)	= 4 +	9		√49 − 2.
8.30. 1) =			3		√9 − 2				;					2)	= 4 +			√49 − 2.
			3				4								7					5
8.31. 1) = −							4	√9 − 2;						2)	= −7 −					5	√36 − 2			.
8.31. 1) = −						3		√9 − 2;						2)	= −7 −						√36 − 2			.
						3												6
							1									8
8.32. 1) = −							1	√36 − 2				;		2)	= 4 −	8		√25 − 2.
8.32. 1) = −						2		√36 − 2				;		2)	= 4 −			√25 − 2.
			7			2									5					2
8.33. 1) =			7		√4 − 2;									2)	= −3 +					2	√36 − 2			.
8.33. 1) =			2		√4 − 2;									2)	= −3 +						√36 − 2			.
			2				3									7		3
8.34. 1) = −							3	√25 − 2				;		2)	= 6 −	7		√4 − 2.
8.34. 1) = −						5		√25 − 2				;		2)	= 6 −			√4 − 2.
			8			5									2					3
8.35. 1) =			8		√49 − 2;									2)	= −7 −					3	√25 − 2			.
8.35. 1) =			7		√49 − 2;									2)	= −7 −						√25 − 2			.
			7															5
														122

	5
8.36. 1) = −	5	√36 − 2	;	2) = 1 + 2√9 − 2.
8.36. 1) = −		√36 − 2	;	2) = 1 + 2√9 − 2.
6

9. Нахождение координат точек пересечения прямой и эллипса

Задание 9. Найти координаты точек пересечения прямой и эллипса.

9.1.3 + 2 = 0, 5 2 + 2 2 + 40 − 24 + 114 = 0.

9.2.4 + + 30 = 0, 2 2 + 2 + 32 − 4 + 114 = 0.

9.3.+ 2 − 1 = 0, 3 2 + 7 2 − 6 − 168 = 0.

9.4.2 + + 12 = 0, 6 2 + 5 2 + 48 + 40 + 150 = 0.

9.5.3 + 2 + 19 = 0, 2 2 + 4 2 + 12 + 40 + 74 = 0.

9.6.+ + 5 = 0, 3 2 + 5 2 + 6 + 40 + 11 = 0.

9.7.2 + 3 − 2 = 0, 2 2 + 2 + 8 − 6 − 2 = 0.

9.8.3 − − 14 = 0, 5 2 + 4 2 + 15 + 40 + 104 = 0.

9.9.2 + + 4 = 0, 2 2 + 2 + 20 − 12 + 62 = 0.

9.10.3 − 2 + 28 = 0, 7 2 + 3 2 + 112 − 12 + 405 = 0.

9.11.+ 3 + 26 = 0, 2 + 2 2 + 4 + 32 + 121 = 0.

9.12.− 2 + 2 = 0, 4 2 + 5 2 + 48 + 20 + 143 = 0.

9.13.+ − 4 = 0, 5 2 + 6 2 − 50 + 12 + 87 = 0.

9.14.+ − 1 = 0, 3 2 + 5 2 + 24 − 50 + 141 = 0.

9.15.+ 2 − 1 = 0, 3 2 + 2 − 30 + 4 + 66 = 0.

9.16.+ + 7 = 0, 3 2 + 4 2 + 24 + 24 + 56 = 0.

9.17.3 − − 27 = 0, 5 2 + 3 2 − 70 + 36 + 321 = 0.

9.18.− 4 + 29 = 0, 2 2 + 5 2 + 36 − 50 + 250 = 0.

9.19.+ 3 + 2 = 0, 3 2 + 5 2 + 30 − 10 + 48 = 0.

9.20.− 3 − 15 = 0, 4 2 + 7 2 + 24 + 56 + 104 = 0.

9.21.+ − 3 = 0, 2 + 2 2 + 4 − 20 + 27 = 0.

9.22.5 + 4 + 11 = 0, 2 2 + 3 2 + 12 − 6 − 86 = 0.

9.23.+ 3 + 13 = 0, 5 2 + 2 2 − 50 + 24 + 150 = 0.

9.24.3 + 4 − 17 = 0, 2 2 + 5 2 + 4 − 50 + 50 = 0.

9.25.3 + 5 + 3 = 0, 3 2 + 2 2 − 24 + 12 − 27 = 0.

9.26.+ − 2 = 0, 4 2 + 3 2 + 24 − 30 + 48 = 0.

9.27.+ 2 + 1 = 0, 4 2 + 5 2 + 24 − 10 − 43 = 0.

9.28.+ 2 + 1 = 0, 5 2 + 3 2 + 50 − 12 + 45 = 0.

9.29.+ 3 − 17 = 0, 2 + 2 2 + 2 − 24 + 62 = 0.

9.30.5 + + 6 = 0, 2 2 + 2 + 4 + 2 − 24 = 0.

9.31.+ 3 − 13 = 0, 2 2 + 3 2 + 8 − 30 + 62 = 0.

9.32.+ − 3 = 0, 3 2 + 5 2 + 6 − 40 + 11 = 0.

9.33.+ 4 + 1 = 0, 4 2 + 5 2 − 24 + 10 − 28 = 0.

9.34.+ 3 − 7 = 0, 3 2 + 7 2 + 12 + 42 + 41 = 0.

9.35.+ 2 − 7 = 0, 6 2 + 7 2 + 12 − 56 + 87 = 0.

9.36.4 − + 15 = 0, 5 2 + 3 2 + 30 + 18 + 19 = 0.

123

10. Составление полярного уравнения эллипса по заданному его каноническому уравнению

Задание 10. Дано каноническое уравнение эллипса. Составить его полярное уравнение, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится: 1) в левом фокусе эллипса; 2) в правом фокусе.


10.1.	2		+		2		= 1.		10.2.	2		+			2		= 1.			10.3.	2		+			2		= 1.
	49				40					56				16							25				8

10.4.	2		+		2		= 1.		10.5.	2		+			2		= 1.			10.6.	2		+			2		= 1.
	64				50					24				16							81				64

10.7.	2		+		2		= 1.		10.8.	2		+			2		= 1.			10.9.	2		+			2		= 1.
	36				18					25				12							50				36

10.10.		2		+		2		= 1.	10.11.		2		+			2		= 1.		10.12.		2		+			2		= 1.
		64				27					16					9						49					28

10.13.		2		+		2		= 1.	10.14.		2			+			2		= 1.	10.15.		2		+			2		= 1.
		81				27					100						75					64					56

10.16.		2		+		2		= 1.	10.17.		2		+			2		= 1.		10.18.		2		+			2		= 1.
		12				4					36					24						25					20

10.19.		2		+		2		= 1.	10.20.		2			+			2		= 1.	10.21.		2		+			2		= 1.
		64				32					100						64					81					63

10.22.		2		+		2		= 1.	10.23.		2		+			2		= 1.		10.24.		2		+			2		= 1.
		49				20					25					4						48					25

10.25.		2		+		2		= 1.	10.26.		2		+			2		= 1.		10.27.		2		+			2		= 1.
		16				4					25					10						49					36

10.28.		2		+		2		= 1.	10.29.		2		+			2		= 1.		10.30.		2		+			2		= 1.
		81				54					36					20						48					28

10.31.		2		+		2		= 1.	10.32.		2		+			2		= 1.		10.33.		2			+			2		= 1.
		16				12					49					24						100						48

10.34.		2		+		2		= 1.	10.35.		2		+			2		= 1.		10.36.		2		+			2		= 1.
		36				12					16					10						81					56

Третий уровень сложности

11. Определение полуосей эллипса по его полярному уравнению Задание 11. Найти полуоси эллипса, заданного полярным уравнением.

11.1. =		12										.							11.2. =		56							.

	3−√							cos												9−5 cos
				3
11.3. =		34													.				11.4. =		10									.
	5−2√									cos										4−√						cos
					2																	11

11.5. =		25√2																	11.6. =		18√10
															.																	.
	8−√									cos										10−√							cos
				14																			10
11.7. =		48												.					11.8. =		18								.

	9−√								cos											5−√					cos
			33																			7
11.9. =		32													.				11.10. =		52												.

	7−√									cos											9−√						cos
				17																				29
11.11. =				20√3													.		11.12. =		4													.

		6−√6 cos																			5−√21 cos

11.13. =		4														.			11.14. =		20										.

		3−√								cos											4−√					cos
							7																		6
11.15. =		28																.	11.16. =		8													.
		5−√									cos										5−√						cos
							11																		17
11.17. =		32											.						11.18. =		24													.

																					5−√						cos
		9−7 cos																							13
11.19. =						√6													11.20. =		21
																.															.
		2−√								cos											3−√					cos
								3																	2

124

11.21. =

11.22. =

4−cos

5−√7 cos

11.23. =

11.24. =

3−cos

4−√7 cos

11.25. =

11.26. =

5−cos

7−cos

11.27. =

11.28. =

10−√

cos

3−2 cos

11.29. =

11.30. =

7−2 cos

3−√5

cos

11.31. =

11.32. =

cos

7−3 cos

6−√15

11.33. =

11.34. =

7−√7 cos

2−cos

11.35. =

11.36. =

11−6√

cos

7−2√

cos

Тесты

Вариант 1

Первый уровень сложности.

1.Уравнение эллипса с центром в точке (−5; −8), полуосями = 7,

= 2, имеет вид (фокусы эллипса лежат на оси абсцисс (ординат) или на

прямой, параллельной этой оси, симметрично относительно точки ):

1)	( −5)2		+	( −8)2	= 1				2)	( −5)2	+	( −8)2	= 1
1)		7	+	2	= 1				2)	49	+	4	= 1
		7		2						49		4
3)	( −5)2		−	( −8)2	= 1				4)	( +5)2	+	( +8)2	= 1
3)	49		−	4	= 1				4)	7	+	2	= 1
	49			4						7		2
5)	( +5)2		+	( +8)2	= 1
5)	49		+	4	= 1
	49			4		2		2
2. Фокусы эллипса						2	+	2	= 1 равны:
2. Фокусы эллипса						64	+	36	= 1 равны:
						64		36
											1(−28; 0), 2(28; 0)
1)	1	(−2√7; 0), 2(2√7; 0)								2)	1(−28; 0), 2(28; 0)
3)	1	(−10; 0), 2(10; 0)								4) 1(−100; 0), 2(100; 0)

5)	1	(0; −2√7), 2(0; 2√7)

Второй уровень сложности.

3. Уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, малая полуось которого равна 3


и эксцентриситет равен					4	, имеет вид:
и эксцентриситет равен					5	, имеет вид:
	2		2		5		2				2				2		2
1)	2	+	2	= 1		2)	2			+	2		= 1	3)	2	−	2	= 1
1)	5	+	3	= 1		2)	25			+	9		= 1	3)	5	−	3	= 1
	5		3				25				9				5		3
4)	2	−	2	= 1		5)			+			= 1
4)	25	−	9	= 1		5)	25		+		9	= 1
	25		9				25				9
								4
4. Уравнение = 1 −								4	√9 − 2 определяет:
4. Уравнение = 1 −									√9 − 2 определяет:
							3

1)эллипс с центром в точке (1; 0), полуосями = 4, = 3, с фокусами, лежащими на оси абсцисс симметрично относительно точки

2)левую половина эллипса с центром в точке (1; 0), полуосями = 4, = 3, с фокусами, лежащими на оси абсцисс симметрично относительно точки

3)правую половина эллипса с центром в точке (1; 0), полуосями

= 4, = 3, с фокусами, лежащими на оси абсцисс симметрично относительно точки

125

4)верхнюю половина эллипса с центром в точке (1; 0), полуосями

= 4, = 3, с фокусами, лежащими на оси абсцисс симметрично относительно точки

5)нижнюю половина эллипса с центром в точке (1; 0), полуосями

= 4, = 3, с фокусами, лежащими на оси абсцисс симметрично относительно точки

Третий уровень сложности.

5. Уравнение эллипса, касающегося двух прямых 3 − 2 − 20 = 0,+ 6 − 20 = 0, при условии, что его оси совпадают с осями координат,

имеет вид:

1)	2	−		2	= 1			2)		2				−	2	= 1				3)	2	+	2		= 1

	40		10							2√10					√10						40		10
	40		10							2√10					√10						40		10
4)	2		+		2	= 1		5)				+			= 1

	2√10				√10				40					10
	2√10				√10				40					10
								Вариант 2
Первый уровень сложности.
1. Дано уравнение эллипса ( + 2)2 +																	( −4)2	= 1. Координаты его
1. Дано уравнение эллипса ( + 2)2 +																9		= 1. Координаты его
																9
центра , полуоси и равны:
1) (2; −4), = 1, = 9													2) (2; −4), = 1, = 3
3)	(−2; 4), = 1, = 9												4) (−2; 4), = 1, = 3
5) (4; −2), = 1, = 3
2. Эксцентриситет эллипса									2		+			2	= 1 равен:
2. Эксцентриситет эллипса									36		+			4	= 1 равен:
									36					4
1)	√10					2)	10	3)		2√2								4)	4			5)		1
1)	3					2)		3)		3								4)				5)
	3					3				3								3					9

Второй уровень сложности.

3. Уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, расстояние между фокусами ко-

торого равно 4√5 и большая полуось равна 4√2, имеет вид:

1)	2	+		2		= 1		2)	2		+			2		= 1	3)	2	−	2	= 1

	32			12					4√2				2√3					32		12
	32			12					4√2				2√3					32		12
4)	2		−		2		= 1	5)		+					= 1

	4√2				2√3				32			12
	4√2				2√3				32			12

4. Прямая + 2 + 5 = 0 пересекает эллипс 2 2 + 3 2 − 4 + 18 + +18 = 0 в следующих точках:

1)прямая проходит вне эллипса

2)прямая касается эллипса в точке (−1; −2)

3)прямая касается эллипса в точке (3; −4)

4) 1(1; 2), 2(−3; 4)	5) 1(−1; −2), 2(3; −4)
Третий уровень сложности.
5. Полуоси эллипса, заданного полярным уравнением =			4	,


			5−√21 cos
равны:
1) = 25, = 4	2) = 5, = 4	3) = 5, = 2

4) = 25, = 16	5) = 5, = √21
	126

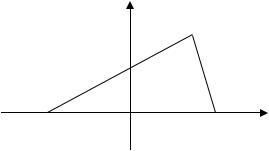
Глава 3. Гипербола

В этой главе будет рассмотрен такой простейший геометрический объект как гипербола. Гипербола – это линия, уравнение которой может

быть записано в виде 2 + 2 + 2 + 2 + 2 + = 0, где , , ,

, , – некоторые числа, причём 2 + 2 + 2 ≠ 0 и − 2 < 0. Указанное уравнение является общим уравнением второй степени. Этому уравнению удовлетворяют координаты и любой точки, лежащей на гиперболе, и не удовлетворяют координаты и ни одной точки, не лежащей на гиперболе.

3.1. Определение гиперболы

Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух фиксированных точек 1 и 2, называемых фокусами, есть величина постоянная, равная 2. Требуется, чтобы эта постоянная была меньше расстояния между фокусами и отлична от нуля. Указанная разность берётся по абсолютной величине.

3.2. Каноническое уравнение гиперболы

Вывод канонического уравнения гиперболы аналогичен выводу канонического уравнения эллипса.

Выберем систему координат так, чтобы ось абсцисс проходила через фокусы, начало координат находилось в середине между фокусами. Расстояние между фокусами обозначим через 2. Пусть (; ) – произвольная точка гиперболы. Обозначим через 1 расстояние от точки до фокуса 1, обозначим через 2 расстояние от точки до фокуса 2. Величины 1 и 2 называют фокальными радиусами точки . Сделаем схематичный чертёж

(рис. 3.1).

1 2

Рис. 3.1. Определение гиперболы

Исходя из определения гиперболы, можно записать:

| 1 − 2| = 2, где 1 – расстояние между точками и 1, 2 – расстояние между точками и 2.

Учитывая, что точки 1 и 2 симметричны относительно начала координат и расстояние между этими точками равно 2, можно записать их координаты: 1(− ; 0), 2(; 0).

127

	Далее, запишем выражение расстояния между точками и 1, ис-
пользуя		формулу	расстояния			между двумя		точками =

√(	−	)2 + ( − )2, где		( ;		) – одна точка, ( ; ) – другая точка.
2	1	2	1	1	1	2	2
Здесь 1 = − , 1 = 0, 2 = , 2 = . Получаем:

	= \| \| = √( + )2			+ ( − 0)2 = √( + )2 + 2.
	1	1
	Аналогично запишем выражение расстояния между точками и 2,
учитывая, что 1 = , 1 = 0, 2 = , 2 = . Получаем:

	= \| \| = √( − )2			+ ( − 0)2 = √( − )2 + 2.
	2	2

Подставим полученные выражения в равенство | 1 − 2| = 2 :

|√( + )2 + 2 − √( − )2 + 2| = 2 .

Раскроем модуль:

√( + )2 + 2 − √( − )2 + 2 = ±2 .

Упростим полученное уравнение. Изолируем первый корень:

√( + )2 + 2 = ±2 + √( − )2 + 2.

Возведём обе части равенства в квадрат:

( + )2 + 2 = 4 2 ± 4 √( − )2 + 2 + ( − )2 + 2.

Раскроем квадраты, стоящие вне корня:

2 + 2 + 2 + 2 = 4 2 ± 4 √( − )2 + 2 + 2 − 2 + 2 + 2.

Часть слагаемых уничтожается. Изолируем корень. Получаем:

±4 √( − )2 + 2 = 4 − 4 2.

Разделим уравнение на 4:

± √( − )2 + 2 = − 2.

Возведём обе части равенства в квадрат:

2(( − )2 + 2) = ( − 2)2.

Раскроем скобки:

2 2 − 2 2 + 2 2 + 2 2 = 2 2 − 2 2 + 4.

Преобразуем:

2 2 − 2 2 + 2 2 = 4 − 2 2,2( 2 − 2) + 2 2 = 2( 2 − 2).

По определению гиперболы | 1 − 2| < 2 . Отсюда 2 < 2 и < ,2 − 2 > 0. Обозначим 2 − 2 через 2: 2 − 2 = 2 или

+ = .

Получена формула, показывающая связь между , и .

Тогда уравнение принимает вид:

− 2 2 + 2 2 = − 2 2, 2 2 − 2 2 = 2 2.

Разделив уравнение на 2 2, получаем:

− = .

Полученное уравнение называется каноническим (простейшим)

уравнением гиперболы.

Величины и называются полуосями гиперболы. Если полуоси гиперболы равны, то есть = , то такая гипербола называется равносто-

128

ронней. Каноническое уравнение равносторонней гиперболы принимает вид: 22 − 22 = 1, 2 − 2 = 2.

3.3. Форма гиперболы

Проанализируем полученное каноническое уравнение и установим форму гиперболы.

1)Так как при замене на – , на – каноническое уравнение гиперболы не меняется, то гипербола симметрична относительно обеих осей координат.

2)Найдём точки пересечения гиперболы с осями координат.

Для нахождения точки пересечения с осью возьмём = 0 и подставим в уравнение гиперболы. Получаем: 22 − 022 = 1, 22 = 1, 2 = 2,

= ± , то есть гипербола пересекает ось в двух точках: 1(− ; 0) и2( ; 0).

Для нахождения точки пересечения с осью возьмём = 0 и подставим в уравнение гиперболы. Получаем: 022 − 22 = 1, 22 = −1, 2 = − 2.

Получили противоречивое равенство, то есть гипербола не пересекает ось

3)Точки 1 и 2 называются вершинами гиперболы. Отрезок 1 2 длины 2 называется действительной осью гиперболы. Отрезок 2 длины

называется действительной полуосью гиперболы. Отрезок 1 2 длины 2 , соединяющий точки 1(0; − ) и 2(0; ), называется мнимой осью гиперболы. Отрезок 2 длины называется мнимой полуосью гиперболы. Прямоугольник со сторонами 2 и 2 называется основным прямоугольником гиперболы.

4)Выразим из канонического уравнения :

22 = 22 − 1, 2 = 2 ( 22 − 1), = ±√ 2 ( 22 − 1) = ± √ 22 − 1 =

= ± √ 2−2 2 = ± √ 2 − 2.

Из уравнения видно, что | | ≥ . Отсюда: ≥ или ≤ − , то есть точки гиперболы расположены слева от прямой, заданной уравнением = − , и справа от прямой, заданной уравнением = . Между прямыми = − и = точек гиперболы нет.

Если приближается к справа или к − слева, то приближается к

Из уравнения также видно, когда по модулю возрастает, то по модулю также возрастает.

3.4. Предварительное построение гиперболы

На основании проведённого исследования изобразим гиперболу. Начнём с построения основного прямоугольника. Для этого отложим по оси от начала координат влево и вправо единиц. Получим вершины

129

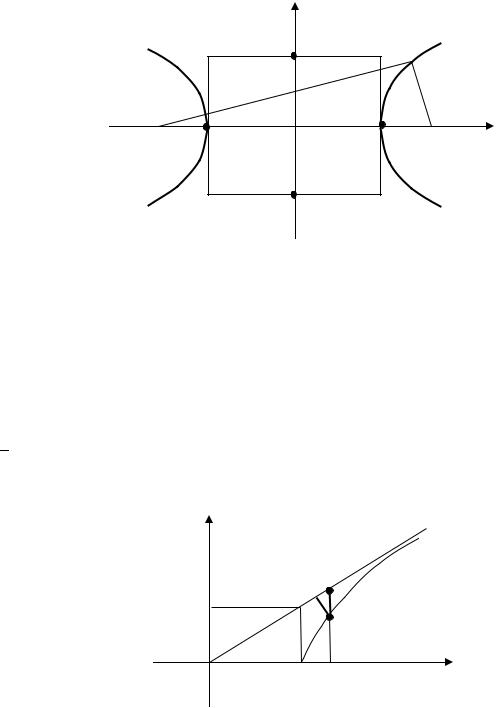
гиперболы – точки 1 и 2. Далее отложим по оси от начала координат вверх и вниз единиц. Получим точки 1 и 2. Точки 1, 2, 1, 2 являются серединами сторон основного прямоугольника. Гипербола представлена двумя ветвями – левой и правой, расположенными за пределами основного прямоугольника (рис. 3.2).


		2
		1
				2
			2
	1
1	−			2

1 −

Рис. 3.2. Предварительное построение гиперболы

3.5. Асимптоты гиперболы

Асимптотой называется прямая, расстояние от которой до точек кривой стремится к нулю при стремлении координаты какой-либо точки к ∞ или к −∞.


Рассмотрим гиперболу, заданную уравнением = +	√2	− 2	.

Пусть (; ) – произвольная точка гиперболы. Рассмотрим прямую =

. Обозначим через расстояние от точки до этой прямой. Возьмём на

прямой точку (; ̅) и найдём расстояние между точками и как разность ординат этих точек (рис. 3.3):

Рис. 3.3. Нахождение асимптот гиперболы

) =

| | =

−

√2 − 2

( − √2 − 2

( −√

)

∙

2−2

)(+√2−2

∙

+√2−2

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3113 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.01.20245.44 Mб0817.pdf
#
09.01.20245.44 Mб0818.pdf
#
09.01.20245.46 Mб1819.pdf
#
09.01.2024441.6 Кб082.pdf
#
09.01.20245.47 Mб0820.pdf
#
09.01.20245.5 Mб6821.pdf
#
09.01.20245.54 Mб0822.pdf
#
09.01.20245.55 Mб2823.pdf
#
09.01.20245.55 Mб0824.pdf
#
09.01.20245.55 Mб0825.pdf
#
09.01.20245.57 Mб2826.pdf