
821
.pdf
Запишем координаты точек и : (− 2 ; ), (2 ; 0). С учётом это-
го запишем расстояние между точками и по формуле расстояния между двумя точками:
= = √( − (− 2))2 + ( − )2 = √( + 2)2.
Аналогично найдём расстояние между точками и :
= = √( − 2)2 + ( − 0)2 = √( − 2)2 + 2.
По определению параболы = . На основании этого можно запи-
сать:
√( − 2)2 + 2 = √( + 2)2.
Возведём обе части равенства в квадрат:
( − 2)2 + 2 = ( + 2)2.
Преобразуем:
2 − + 42 + 2 = 2 + + 42 ,= .
Полученное уравнение называется каноническим (простейшим)
уравнением параболы.
4.3. Форма параболы
Проанализируем полученное каноническое уравнение и установим форму параболы.
1)Так как при замене на – каноническое уравнение параболы не меняется, то парабола симметрична относительно оси .
2)Найдём точки пересечения параболы с осями координат.
Для нахождения точки пересечения с осью возьмём = 0 и подставим в уравнение параболы. Получаем: 02 = 2 , = 0, то есть парабола пересекает ось в точке: (0; 0).
Для нахождения точки пересечения с осью возьмём = 0 и подставим в уравнение параболы. Получаем: 2 = 2 ∙ 0, = 0, то есть парабола пересекает ось в точке: (0; 0). Точка (0; 0) называется вершиной параболы.
Таким образом, парабола пересекает обе оси в начале координат.
3)Из канонического уравнения параболы следует, что ≥ 0, поэтому парабола расположена справа от оси .
4)Если возрастает, то по модулю также возрастает.
4.4. Построение параболы
На основании проведённого исследования изобразим параболу. Сначала построим фокус параболы: точку (2 ; 0) и построим директрису:
191
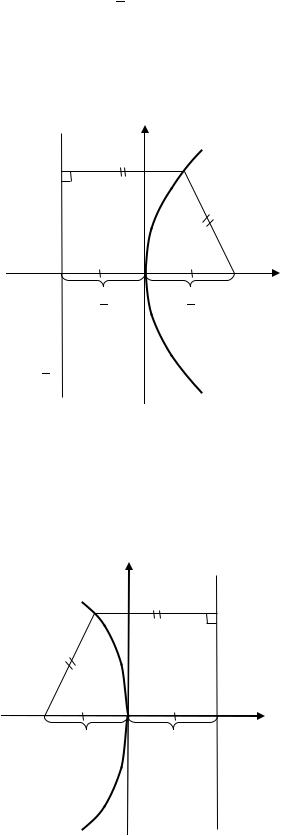
прямую, заданную уравнением = − 2 . Затем «на глаз» отметим точку с
неотрицательной абсциссой так, чтобы расстояние от этой точки до фокуса было равно расстоянию от этой же точки до директрисы. Затем проведём одну линию из начало координат через точку и вторую линию, симметричную первой относительно оси (рис. 4.2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
||
2 |
2 |
|
|
= − 2
Рис. 4.2. Форма параболы, заданной уравнением 2 = 2
Уравнение = − также является каноническим (простейшим) уравнением параболы, симметричной относительно оси , с вершиной в начале координат и расположенной слева от оси . В этом случае фокус
(− |
|
; 0) и директриса задана уравнением = |
|
(рис. 4.3). |
||||||||
|
|
|||||||||||
2 |
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Рис. 4.3. Форма параболы, заданной уравнением 2 = −2
Уравнение = тоже является каноническим (простейшим)
уравнением параболы, симметричной относительно оси , с вершиной в
192
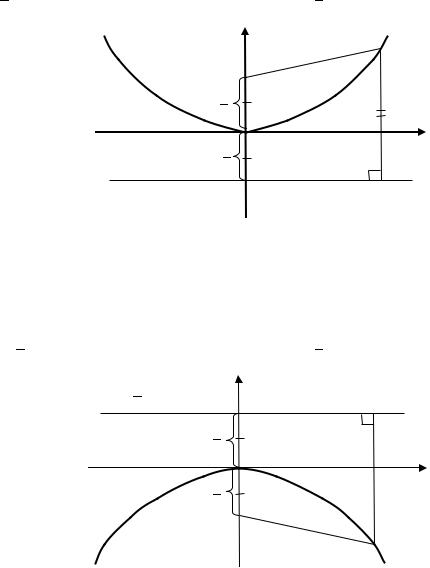
начале координат и расположенной выше оси . В этом случае фокус(0; 2) и директриса задана уравнением = − 2 (рис. 4.4).
2
2


|
|
|
= − |
|
|
|
|
|||
2 |
|||
|
Рис. 4.4. Форма параболы, заданной уравнением 2 = 2
Уравнение = − тоже является каноническим (простейшим)
уравнением параболы, симметричной относительно оси , с вершиной в начале координат и расположенной ниже оси . В этом случае фокус
(0; − 2) и директриса задана уравнением = 2 (рис. 4.5).
= 2
2
2



Рис. 4.5. Форма параболы, заданной уравнением 2 = −2
Если уравнение параболы записано в виде ( − 0)2 = 2( − 0)2, то его можно привести к каноническому уравнению с помощью формул
преобразования координат при параллельном сдвиге осей: { ′ = − 0,′ = − 0.
Здесь (; ) – новое начало координат; – старая система координат, ′ ′ – новая система координат; , – старые координаты; ′, ′ – новые координаты. Подставим в уравнение параболы формулы преобразования координат. Получаем: ′2 = 2′2. Вершина такой параболы нахо-
дится в точке ( 0; 0) (рис. 4.6).
Уравнение параболы, записанное в виде
( − ) = ( − ) ,
называют нормальным уравнением параболы. Оно представляет параболу с вершиной в точке ( 0; 0), осью симметрии, параллельной оси абсцисс и ветвями, направленными вправо.
193

|
′ |
|
0
2 2
0
= 0 − 2
′
Рис. 4.6. Форма параболы, заданной уравнением ( − 0)2 = 2 ( − 0)
Аналогично можно записать остальные нормальные уравнения параболы:
( − ) = − ( − ) – парабола с вершиной в точке ( 0; 0), осью симметрии, параллельной оси абсцисс и ветвями, направленными
влево;
( − ) = ( − ) – парабола с вершиной в точке ( 0; 0), осью симметрии, параллельной оси ординат и ветвями, направленными
вверх;
( − ) = − ( − ) – парабола с вершиной в точке ( 0; 0), осью симметрии, параллельной оси ординат и ветвями, направленными
вниз.
4.5.Эксцентриситет параболы
Впредыдущих главах, посвящённых эллипсу и гиперболе, была рассмотрена теорема о постоянстве отношения расстояния от произвольной точки эллипса или гиперболы до фокуса к расстоянию от этой же точки до соответствующей этому фокусу директрисы. Это отношение равно эксцентриситету эллипса или гиперболы. Это свойство можно положить в основу определения этих кривых. Положим это же свойство в основу определения параболы. Так как для параболы отношение расстояния от произвольной точки до фокуса равно расстоянию от этой же точки до директрисы, то экс-
центриситет параболы равен 1: = 1.
Пример 4.1. Составить каноническое или нормальное уравнение па-
раболы с вершиной в точке и параметром , если фокус параболы лежит на оси абсцисс (ординат) или на прямой, параллельной этой оси:
1) (0; 0), = 5. Ветви направлены вправо.
194

2)(0; 0), = 3. Ветви направлены влево.
3)(0; 0), = 72 . Ветви направлены вверх.
4)(0; 0), = 83 . Ветви направлены вниз.
5)(7; 0), = 52 . Ветви направлены влево.
6)(0; −4), = 4. Ветви направлены вправо.
7)(2; −6), = 12 . Ветви направлены вниз.
8)(− 58 ; 13), = 1. Ветви направлены вверх.
9)(−10; −11), = 89 . Ветви направлены влево.
10)(103 ; − 53), = 16 . Ветви направлены вверх.
Решение.
1)Воспользуемся каноническим уравнением параболы с ветвями, направленными вправо и параметром : 2 = 2 . В условиях примера = 5. Подставляем это значение в каноническое уравнение параболы. Получаем: 2 = 2 ∙ 5 ∙ . Преобразуем: 2 = 10 .
2)Воспользуемся каноническим уравнением параболы с ветвями,
направленными влево и параметром : 2 = −2 . В условиях примера = = 3. Подставляем это значение в каноническое уравнение параболы. Получаем: 2 = −2 ∙ 3 ∙ . Преобразуем: 2 = −6 .
3) Воспользуемся каноническим уравнением параболы с ветвями, направленными вверх и параметром : 2 = 2 . В условиях примера = 72
. Подставляем это значение в каноническое уравнение параболы. Получаем:
2 = 2 ∙ 72 ∙ . Преобразуем: 2 = 7 .
4) Воспользуемся каноническим уравнением параболы с ветвями, направленными вниз и параметром : 2 = −2 . В условиях примера =
83 . Подставляем это значение в каноническое уравнение параболы. Получаем: 2 = −2 ∙ 83 ∙ . Преобразуем: 2 = − 163 .
5) Воспользуемся нормальным уравнением параболы, с вершиной в
точке ( 0; 0), ветвями, направленными влево и параметром :
( − 0)2 = −2 ( − 0). В условиях примера 0 = 7, 0 = 0, = 52 . Под-
ставляем эти значения в нормальное уравнение параболы. Получаем:
( − 0)2 = −2 ∙ 52 ∙ ( − 7). Преобразуем: 2 = −5( − 7).
6) Воспользуемся нормальным уравнением параболы, с вершиной в
точке ( 0; 0), ветвями, направленными вправо и параметром :
( − 0)2 = 2 ( − 0). В условиях примера 0 = 0, 0 = −4, = 4. Под-
ставляем эти значения в нормальное уравнение параболы. Получаем:
( − (−4))2 = 2 ∙ 4 ∙ ( − 0). Преобразуем: ( + 4)2 = 8 .
7) Воспользуемся нормальным уравнением параболы, с вершиной в точке ( 0; 0), ветвями, направленными вниз и параметром :
195

( − 0)2 = −2 ( − 0). В условиях примера 0 = 2, 0 = −6, = 12 .
Подставляем эти значения в нормальное уравнение параболы. Получаем:
( − 2)2 = −2 ∙ |
1 |
∙ ( − (−6)). Преобразуем: ( − 2)2 |
= −( + 6). |
||||||||||||||||
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8) Воспользуемся нормальным уравнением параболы, с вершиной в |
|||||||||||||||||||
точке ( 0; 0), ветвями, направленными вверх и параметром : |
|
|
|
||||||||||||||||
( − )2 |
= 2 ( − ). В условиях примера = − |
5 |
, |
= |
1 |
|
, = 1. Под- |
||||||||||||
|
|
||||||||||||||||||
0 |
|
0 |
|
|
0 |
|
|
8 |
0 |
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ставляем |
эти значения |
в |
нормальное уравнение |
параболы. |
Получаем: |
||||||||||||||
|
5 |
2 |
|
|
|
1 |
|
5 |
2 |
|
|
1 |
|
|
|
||||
( − (− |
|
)) = 2 ∙ 1 ∙ ( − |
|
). Преобразуем: ( + |
|
) |
= 2 ( − |
|
). |
|
|
|
|||||||
8 |
3 |
8 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||
9) Воспользуемся нормальным уравнением параболы, с вершиной в |
|||||||||||||||||||
точке ( 0; 0), ветвями, направленными влево и параметром : |
|
9 |
|
||||||||||||||||
( − )2 |
= −2 ( − ). В условиях примера |
|
= −10, |
= −11, = |
. |
||||||||||||||
|
|
||||||||||||||||||
0 |
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
8 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляем эти значения в нормальное уравнение параболы. |
Получаем: |
||||||||||||||||||
8∙ ( − (−10)). Преобразуем: ( + 11)2 =
=− 49 ( + 10).
10)Воспользуемся нормальным уравнением параболы, с вершиной в92
точке ( 0; 0), ветвями, направленными вверх и параметром :
( − 0)2 = 2 ( − 0). В условиях примера 0 = 103 , 0 = − 53 , = 16 .
Подставляем эти значения в нормальное уравнение параболы. Получаем:
( − 103 )2 = 2 ∙ 16 ∙ ( − (− 53)). Преобразуем: ( − 103 )2 = 13 ( + 53).
Ответ: 1) 2 = 10 ; 2) 2 = −6 ; 3) 2 = 7 ; 4) 2 = − 163 ; 5) 2 = −5( − 7); 6) ( + 4)2 = 8 ; 7) ( − 2)2 = −( + 6); 8) ( + 58)2 = = 2 ( − 13); 9) ( + 11)2 = − 49 ( + 10); 10) ( − 103 )2 = 13 ( + 53).
Пример 4.2. Определить координаты вершины, параметр и направление осей параболы по её каноническому или нормальному уравнению:
1) 2 = 6 ; |
|
|
2) 2 = 13 ; |
|
|
|
|
|||||||
3) 2 = −2 ; |
|
|
4) 2 = − |
15 |
; |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
8 |
|
|
|
|
|
|||||
5) ( − 5)2 = −4( + 2); |
6) 2 = 7( + 8); |
|
|
|
||||||||||
7) |
( + 2)2 = |
20 |
( − 9); |
8) ( − |
1 |
)2 = −4 ; |
||||||||
7 |
|
|||||||||||||
|
|
|
6 |
|
|
)2 = |
|
|
|
|
||||
9) |
2 = + 1; |
|
10) ( + |
5 |
16 |
( + |
18 |
). |
||||||
|
|
9 |
|
|||||||||||
|
|
|
|
14 |
|
|
5 |
|
||||||
Решение.
1)Сравним данное уравнение с каноническим уравнением параболы
спараметром и ветвями, направленными вправо: 2 = 2 . Преобразуем данное уравнение: 2 = 2 ∙ 3 ∙ . Вершина параболы находится в точке(0; 0), параметр = 3, ветви направлены вправо.
2)Сравним данное уравнение с каноническим уравнением параболы
спараметром и ветвями, направленными вверх: 2 = 2 . Преобразуем
196

данное уравнение: 2 = 2 ∙ 132 ∙ . Вершина параболы находится в точке
(0; 0), параметр = 132 , ветви направлены вверх.
3)Сравним данное уравнение с каноническим уравнением параболы с параметром и ветвями, направленными вниз: 2 = −2 . Преобразуем данное уравнение: 2 = −2 ∙ 1 ∙ . Вершина параболы находится в точке
(0; 0), параметр = 1, ветви направлены вниз.
4)Сравним данное уравнение с каноническим уравнением параболы
с параметром и ветвями, направленными влево: 2 = −2 . Преобразуем данное уравнение: 2 = −2 ∙ 1516 ∙ . Вершина параболы находится в точке
(0; 0), параметр = 1516 , ветви направлены влево.
5)Сравним данное уравнение с нормальным уравнением параболы с
вершиной в точке ( 0; 0), параметром и ветвями, направленными вниз: ( − 0)2 = −2 ( − 0). Преобразуем данное уравнение: ( − 5)2 =
= −2 ∙ 2 ∙ ( − (−2)). Вершина параболы находится в точке (5; −2), параметр = 2, ветви направлены вниз.
6) Сравним данное уравнение с нормальным уравнением параболы с вершиной в точке ( 0; 0), параметром и ветвями, направленными
вправо: ( − )2 = 2 ( − ). Преобразуем данное уравнение: ( − 0)2 = |
||||||||
|
7 |
0 |
|
0 |
|
|||
= 2 ∙ |
∙ ( − (−8)). |
Вершина параболы находится в точке (−8; 0), пара- |
||||||
|
||||||||
2 |
|
7 |
|
|
|
|
||
метр = |
, ветви направлены вправо. |
|||||||
|
||||||||
|
|
2 |
|
|
|
|
||
|
|
7) Сравним данное уравнение с нормальным уравнением параболы с |
||||||
вершиной в точке ( 0; 0), |
параметром и ветвями, направленными |
|||||||
вверх: |
( − )2 = 2 ( − ). Преобразуем данное уравнение: |
|||||||
|
|
0 |
|
0 |
|
|||
( − (−2))2 = 2 ∙ |
10 |
∙ ( − 9). |
Вершина параболы находится в точке |
|||||
|
||||||||
|
|
7 |
|
|
||||
(−2; 9), параметр = 107 , ветви направлены вверх.
8) Сравним данное уравнение с нормальным уравнением параболы с
вершиной в точке ( 0; 0), параметром и ветвями, направленными влево: ( − 0)2 = −2 ( − 0). Преобразуем данное уравнение:
( − 16)2 = −2 ∙ 2 ∙ ( − 0). Вершина параболы находится в точке (0; 16),
параметр = 2, ветви направлены влево.
9) Сравним данное уравнение с нормальным уравнением параболы с
вершиной в точке ( 0; 0), параметром и ветвями, направленными вверх: ( − 0)2 = 2 ( − 0). Преобразуем данное уравнение: ( − 0)2 =
= 2 ∙ 12 ∙ ( − (−1)). Вершина параболы находится в точке (0; −1), пара-
метр = 12 , ветви направлены вверх.
10) Сравним данное уравнение с нормальным уравнением параболы с вершиной в точке ( 0; 0), параметром и ветвями, направленными вправо: ( − 0)2 = 2 ( − 0). Преобразуем данное уравнение:
197
|
|
|
5 |
2 |
|
|
8 |
|
|
|
18 |
|
|
|
|
|
|||
( − (− |
)) = 2 ∙ |
∙ ( − (− |
)). Вершина параболы находится в точке |
||||||||||||||||
|
|
|
|||||||||||||||||
14 |
9 |
5 |
|
|
|
|
|
||||||||||||
(− |
18 |
; − |
|
5 |
), параметр = |
8 |
, ветви направлены вправо. |
||||||||||||
|
14 |
|
|||||||||||||||||
5 |
|
|
|
|
|
|
9 |
|
|
|
|
|
13 |
|
|||||
|
Ответ: 1) (0; 0), = 3, ветви направлены вправо; 2) (0; 0), = |
, |
|||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
ветви направлены вверх; 3) (0; 0), = 1, ветви направлены вниз; |
|||||||||||||||||||
4) (0; 0), = |
15 |
, |
ветви направлены влево; 5) (5; −2), = 2, ветви |
||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
16 |
|
|
|
|
|
|
|
7 |
|
|
|
||||
направлены вниз; 6) (−8; 0), = |
, ветви направлены вправо; 7) (−2; 9), |
||||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
= |
10 |
, ветви направлены вверх; 8) (0; |
1 |
), = 2, ветви направлены влево; |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
7 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9) (0; −1), = |
1 |
, ветви направлены вверх; 10) (− |
18 |
; − |
5 |
), = |
8 |
, ветви |
||||||||||||||||||
|
|
|
|
9 |
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
5 |
14 |
|
|
||||||||||||
направлены вправо. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример. 4.3. Построить параболу по её каноническому или нормаль- |
||||||||||||||||||||||||
ному уравнению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1) |
2 = 2 ; |
2) |
2 |
= −15 ; |
|
|
|
|
|
|
|
|||||||||||||
|
|
3) |
2 = −20 ; |
4) |
2 |
= 8 ; |
|
|
|
|
|
|
|
|||||||||||||
|
|
5) |
( − 3)2 = −21( + 5); |
6) |
2 |
= 6( − 4); |
|
|
|
|
|
|
|
|||||||||||||
|
|
7) |
( + 2)2 = − 2; |
8) |
( − |
21 |
)2 = −10( + 3); |
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
)2 = |
|
|
|
|
|
|
5 |
|
)2 = −5√5 |
|
|
|
|
|
|
||||||
|
|
9) |
( + |
19 |
36 |
( + 2); |
10) ( − |
100 |
|
. |
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
3 |
19 |
31 |
|
|
||||||||||||||||||||
Решение.
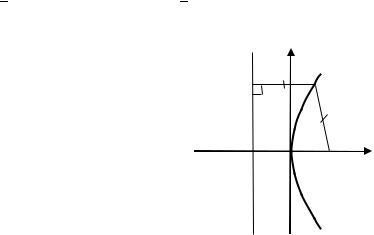
1) 2 = 2 . Преобразуем уравнение: 2 = 2 ∙ 1 ∙ . Вершина находится в точке (0; 0), ветви направлены вправо, параметр = 1, фокус
(12 ; 0), директриса = − 12 (рис. 4.7).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
= − |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рис. 4.7. Парабола с вершиной в точке (0; 0) и параметром = |
1 |
|
|
|||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
(к Примеру 4.3 (1)) |
|
|
|
|
|
|
|
|
||||
|
2) 2 = −15 . Преобразуем уравнение: |
2 |
= −2 ∙ |
15 |
∙ . Вершина |
|||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
15 |
|
||||
находится в точке (0; 0), ветви направлены влево, |
параметр = |
, фокус |
||||||||||||||
|
||||||||||||||||
|
15 |
|
15 |
|
|
|
|
|
|
|
2 |
|
|
|||
(− |
; 0), директриса = |
(рис. 4.8). |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
198 |
|
|
|
|
|
|
|
|
|
|||||

|
|
|
= 154
Рис. 4.8. Парабола с вершиной в точке (0; 0) и параметром = 7,5 (к Примеру 4.3 (2))
3) 2 = −20 . Преобразуем уравнение: 2 = −2 ∙ 10 ∙ . Вершина находится в точке (0; 0), ветви направлены вниз, параметр = 10, фокус(0; −5), директриса = 5 (рис. 4.9).
|
|
= 5 |
|
|
|
|
|
Рис. 4.9. Парабола с вершиной в точке (0; 0) и параметром = 5 (к Примеру 4.3 (3))
4) 2 = 8 . Преобразуем уравнение: 2 = 2 ∙ 4 ∙ . Вершина находится в точке (0; 0), ветви направлены вверх, параметр = 4, фокус (0; 2), директриса = −2 (рис. 4.10).
|
|
|
|
|
|
= −2
Рис. 4.10. Парабола с вершиной в точке (0; 0) и параметром = 4 (к Примеру 4.3 (4))
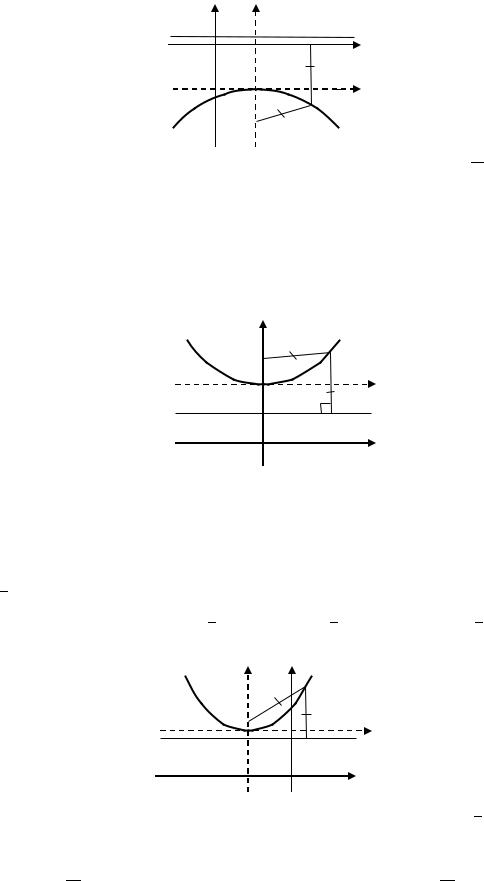
5)( − 3)2 = −21( + 5). Преобразуем уравнение: ( − 3)2 =
=−2 ∙ 212 ∙ ( + 5). Вершина параболы находится в точке (3; −5), ветви
направлены вниз, параметр = |
21 |
, фокус |
(3; − |
41 |
), |
директриса = |
1 |
|
|
|
|
||||||
2 |
|
4 |
|
4 |
||||
(рис. 4.11). |
|
|
|
|
|
|
|
|
|
|
199 |
|
|
|
|
|
|
|
′ |
= |
1 |
|
|
|
|
|
|
|
|
4 |
||
|
|
|
||
|
3 |
|
|
|
−5 |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
Рис. 4.11. Парабола с вершиной в точке (3; −5) и параметром = 212 (к Примеру 4.3 (5))
6) 2 = 6( − 4). Преобразуем уравнение: ( − 0)2 = 2 ∙ 3 ∙ ( − 4).
Вершина параболы находится в точке (0; 4), ветви направлены вверх, па-
раметр = 3, фокус (0; |
11 |
), директриса = |
5 |
|
(рис. 4.12). |
|||||
2 |
|
|||||||||
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
, ′ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
|
4 |
|
|
|
′ |
||
|
|
|
|
|
|
|||||
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.12. Парабола с вершиной в точке (0; 4) и параметром = 3 (к Примеру 4.3 (6))
7)( + 2)2 = − 2. Преобразуем уравнение: ( − (−2))2 =
=2 ∙ 12 ∙ ( − 2). Вершина параболы находится в точке (−2; 2), ветви
направлены вверх, параметр = 12 , фокус (−2; 49), директриса = 74
(рис. 4.13).
|
|
|
′ |
|
|
|
|
|
|
|
|
= |
3 |
|
2 |
′ |
|
|
|
|
|
|
|
4 |
|
|
|
||
|
|
|
−2 |
|
|
Рис. 4.13. Парабола с вершиной в точке (−2; 2) и параметром = 12 (к Примеру 4.3 (7))
8) ( − 215 )2 = −10( + 3). Преобразуем уравнение: ( − 215 )2 =
200
