
821
.pdf
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
ляет гиперболу. Преобразуем уравнение: |
|
|
− |
|
|
= 1. Полуоси гиперболы |
|||||||||||||||||||
4 |
2 |
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
= 4, = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) |
|
2 |
− |
2 |
= −1. Сравнивая данное уравнение с каноническим урав- |
||||||||||||||||||||
8 |
24 |
||||||||||||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нением |
гиперболы |
|
− |
|
= −1, устанавливаем, |
что |
данное уравнение |
||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||
определяет гиперболу. Преобразуем уравнение: |
|
2 |
|
|
− |
2 |
|
= 1. Полуоси |
|||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2√2) |
|
|
(2√6) |
|
|
||||||
гиперболы = 2√2, = 2√6.
4)4 2 − 9 2 = 25. Разделим уравнение на 25. Получаем: 4252 − 9252 =
=1. Разделим числитель и знаменатель первой дроби на 4, второй дроби –
на 9. Получаем: 252 − 252 = 1. Сравнивая данное уравнение с каноническим
4 9
уравнением гиперболы 22 − 22 = 1, устанавливаем, что данное уравнение
определяет гиперболу. Преобразуем уравнение: 22 − 22 = 1. Полуоси ги-
(52) (53)
перболы = 52 , = 53 .
5) 2 + 2 = 1. Сравнивая данное уравнение с каноническим уравнением гиперболы 22 − 22 = 1, устанавливаем, что данное уравнение не опре-
деляет гиперболу, так как в уравнении гиперболы между квадратами стоит знак минус, а в данном уравнении стоит знак плюс. Оно представляет окружность, которая была рассмотрена выше.
6) 2 − |
2 |
= 1. Представим уравнение в виде: |
2 |
− |
2 |
|
= 1. Сравнивая |
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
данное уравнение с каноническим уравнением гиперболы |
2 |
− |
|
2 |
|
|
= 1, уста- |
||||||||||||||||||||||
2 |
|
|
2 |
|
|
||||||||||||||||||||||||
навливаем, |
что |
данное |
уравнение определяет гиперболу. |
Преобразуем |
|||||||||||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
уравнение: |
|
|
− |
|
|
|
|
= 1. Полуоси гиперболы = 1, = √5. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
(√5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7) 4 2 |
− 7 2 = 1. Представим 4 следующим образом: |
4 = |
|
1 |
. Анало- |
||||||||||||||||||||||||
1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
||
гично представим 7: 7 = |
|
. Исходное уравнение принимает вид: |
|
|
− |
|
= |
||||||||||||||||||||||
1 |
|
1 |
1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
7 |
|
||||
= 1. |
Сравнивая данное уравнение с каноническим уравнением гиперболы |
||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
− |
|
= 1, |
устанавливаем, |
что данное уравнение определяет гиперболу. |
||||||||||||
2 |
2 |
||||||||||||||||
Преобразуем уравнение: |
2 |
− |
|
2 |
|
= 1. Полуоси гиперболы = |
1 |
, = |
√7 |
. |
|||||||
2 |
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
(1) |
|
( |
√ |
7 |
) |
|
|
2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
7 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
8) 2 |
= 3 − 6. Сравнивая данное уравнение с каноническим уравне- |
||||||||||||||
нием гиперболы 22 − 22 = 1, устанавливаем, что данное уравнение не опре-
деляет гиперболу, так как содержит квадрат только одной переменной. Оно представляет параболу, которая будет рассмотрена позже.
9) 3 − 2 + 4 = 0. Сравнивая данное уравнение с каноническим уравнением гиперболы 22 − 22 = 1, устанавливаем, что данное уравнение не
141

определяет гиперболу, так как не содержит квадраты переменных. Оно представляет прямую.
10) − 5 = 0. Сравнивая данное уравнение с каноническим уравнением гиперболы 22 − 22 = 1, устанавливаем, что данное уравнение не опре-
деляет гиперболу, так как не содержит квадраты переменных. Оно представляет прямую, параллельную оси и отсекающей на оси отрезок
= 5.
Ответ: 2), = 4, = 3; 3), = 2√2, = 2√6; 4), = 52 , = 53 ; 6), = 1, = √5; 7), = 12 , = √77 .
Пример. 3.5. Установить, какие линии определяются следующими
уравнениями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1) = − |
√ |
2 − 16 |
; |
|
|
|
|
|
2) = |
|
√ 2 − 100; |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3) = |
√ 2 |
+ 25; |
|
|
|
|
|
|
|
4) = − |
√ |
2 + 4 |
; |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
5) = −4 + |
√ 2 |
− 36; |
|
6) = − |
√ 2 + 4 + 29; |
|
|||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
5 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
7) = −5 + |
√ |
2 |
− 6 + 45. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
≤ 0, |
|
|
|
||||||||||||||||||||||||||
|
|
|
1) |
= − |
√ |
2 − 16 |
. Запишем ограничения: |
{ |
|
|
|
|
Отсюда: |
|||||||||||||||||||||||||||||||
|
|
|
|
2 − 16 ≥ 0. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
{ |
|
|
|
≤ 0, |
|
|
|
|
Возведём обе части уравнения в квадрат: 2 = |
|
||||||||||||||||||||||||||||||||||
(−∞; −4] [4; ∞). |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
9 |
( 2 |
− 16). Преобразуем: 2 = |
9 |
2 |
− 9, |
9 |
2 |
|
− 2 = 9, |
2 |
|
− |
2 |
|
= 1. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
16 |
|
|
|
|
|
16 |
|
9 |
|
|
|||||||||||||||
Полученное уравнение определяет гиперболу с центром в точке (0; 0) и полуосями = 4, = 3. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет часть гиперболы, расположенной в нижней полуплоскости (рис. 3.17).
|
|
|
7 |
|
|
|
|
|
|
|
≥ 0, |
|
|
|
|||||
|
|
2) = |
√ 2 − 100. Запишем ограничения: { |
|
2 |
Отсюда: |
|||||||||||||
|
|
|
|
− 100 ≥ 0. |
|||||||||||||||
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
||||||
{ |
|
≥ 0, |
Возведём обе части уравнения в квадрат: 2 = |
||||||||||||||||
(−∞; −10] [10; ∞). |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
49 |
( 2 − 100). |
Преобразуем: 2 = |
49 |
2 − 49, |
2 |
− |
49 |
2 = −49, |
2 |
− |
|||||||||
100 |
100 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
100 |
|
49 |
|
||||||
1002 = −1. Полученное уравнение определяет гиперболу с центром в точке
(0; 0) и полуосями = 7, = 10. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет часть гиперболы, расположенной в правой полуплоскости (рис. 3.18).
|
|
9 |
|
|
|
|
|
≥ 0, |
|
|
|
|
3) = |
√ 2 + 25. Запишем ограничения: |
{ |
2 |
|
Отсюда: |
|||||
|
|
+ 25 ≥ |
0. |
||||||||
|
5 |
|
|
|
|
|
|
||||
{ |
≥ 0, |
Возведём обе части уравнения в квадрат: 2 = |
81 |
( 2 + 25). |
|||||||
(−∞; ∞). |
|
||||||||||
|
|
|
|
|
|
25 |
|
|
|||
|
|
|
142 |
|
|
|
|
|
|
||
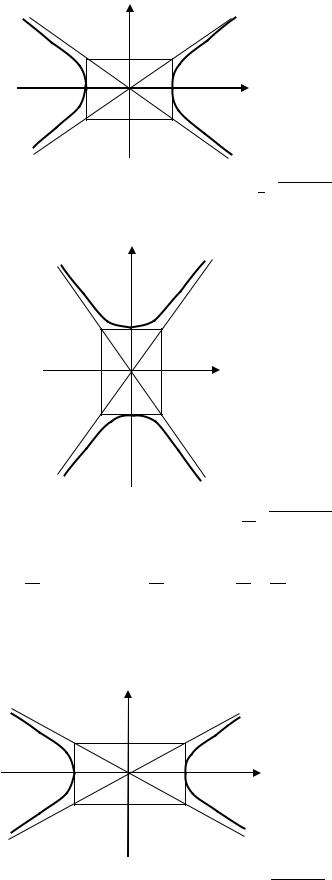
3
−4 |
|
4 |
|
|
|
|
|
|
|
−3 |
|
Рис. 3.17. Линия, заданная уравнением = − 34 √ 2 − 16 (к Примеру 3.5 (1))
|
|
|
|
|
|
10 |
|
−7 |
|
7 |
|
|
|
|
|
|
|
−10 |
|
Рис. 3.18. Линия, заданная уравнением = 107 √ 2 − 100 (к Примеру 3.5 (2))
Преобразуем: 2 = 8125 2 + 81, 2 − 8125 2 = 81, 812 − 252 = 1. Полученное уравнение определяет гиперболу с центром в точке (0; 0) и полуосями
= 9, = 5. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет часть гиперболы, расположенной в правой полуплоскости (рис. 3.19).
|
|
|
|
|
|
5 |
|
−9 |
|
9 |
|
|
|
|
|
|
|
−5 |
|
Рис. 3.19. Линия, заданная уравнением = 59 √ 2 + 25 (к Примеру 3.5 (3))
143

|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
≤ 0, |
|
||
|
4) = − |
√ |
2 |
+ 4. Запишем |
ограничения: |
{ |
|
Отсюда: |
||||||||||
|
|
2 + 4 ≥ 0. |
||||||||||||||||
|
≤ 0, |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
{ |
Возведём обе части |
уравнения в квадрат: 2 = |
1 |
( 2 + 4). |
||||||||||||||
(−∞; ∞). |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||
Преобразуем: |
2 = |
1 |
2 + 1, |
1 |
2 − 2 = −1, |
2 |
− |
2 |
= −1. Полученное |
|||||||||
|
|
|
1 |
|||||||||||||||
|
|
4 |
4 |
4 |
|
|
|
|
||||||||||
уравнение определяет гиперболу с полуосями = 2, |
= 1. Учитывая по- |
|||||||||||||||||
лученные выше ограничения, заключаем, что исходное уравнение определяет часть гиперболы, расположенной в нижней полуплоскости (рис. 3.20).
1
−2 |
|
2 |
|
|
|
|
 −1
−1
Рис. 3.20. Линия, заданная уравнением = 12 √ 2 + 4 (к Примеру 3.5 (4))
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
√ |
|
. Запишем |
||||
|
|
|
5) = −4 + |
√ 2 − 36. Преобразуем: + 4 = |
2 − 36 |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
+ 4 ≥ 0, |
|
|
|
|
|
|
|
|
≥ −4, |
|
|
|
|
||||||
ограничения: { 2 − 36 ≥ 0. |
Отсюда: { (−∞; −6] [6; ∞). Возведём обе |
|||||||||||||||||||||
части уравнения в квадрат: ( + 4)2 |
= |
9 |
( 2 |
− 36). Преобразуем: ( + 4)2 = |
||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
= |
9 |
2 |
− 81, ( + 4)2 − |
9 |
2 |
= −81, |
|
( +4)2 |
− |
2 |
= −1. |
Полученное уравне- |
||||||||||
|
|
81 |
|
|||||||||||||||||||
4 |
4 |
|
|
|
36 |
(−4; 0) полуосями = 9, |
||||||||||||||||
ние определяет гиперболу с центром в точке |
||||||||||||||||||||||
= 6. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет часть гиперболы, расположенной правее прямой = −4 (рис. 3.21).
|
6 |
|
|
−13 |
−4 |
5 |
|
|
|
|
|
|
−6 |
|
|
Рис. 3.21. Линия, заданная уравнением = −4 + 32 √ 2 − 36. (к Примеру 3.5 (5))
144

|
|
|
4 |
|
|
|
|
|
|
|
|
|
≤ 0, |
|||
|
|
6) = − |
√ 2 |
+ 4 + 29. Запишем ограничения: { |
|
2 |
|
|||||||||
|
|
|
|
+ 4 + 29 ≥ 0. |
||||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||
Отсюда: { |
≤ 0, |
|
Возведём обе части уравнения в квадрат: 2 = |
|||||||||||||
(−∞; ∞). |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
16 |
( 2 + 4 + 29). Преобразуем: 25 2 = 16( 2 + 4 + 29), 25 2 = |
||||||||||||||
|
||||||||||||||||
25 |
|
|
|
|
|
|
|
|
2 |
|
( +2)2 |
|
||||
= 16[( + 2)2 + 25], |
25 2 − 16( + 2)2 = 16 ∙ 25, |
− |
= 1. Полу- |
|||||||||||||
|
|
25 |
||||||||||||||
|
|
|
|
|
|
|
|
16 |
|
|
|
|||||
ченное уравнение определяет гиперболу с центром в точке (0; −2) полу-
осями = 4, = 5. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет левую ветвь гиперболы (рис. 3.22).
3
|
|
|
|
−4 |
−2 |
4 |
|
|
|
|
|
|
|
|
|
−7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||
Рис. 3.22. Линия, заданная уравнением = − |
√ 2 + 4 + 29 |
|||||||||||||
5 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(к Примеру 3.5 (6)) |
|
|
|
|
|
|
|
|
||
|
2 |
|
|
. Преобразуем: + 5 = |
2 |
√ |
|
. |
||||||
7) = −5 + |
√ |
2 |
− 6 + 45 |
2 − 6 + 45 |
||||||||||
|
|
|||||||||||||
3 |
|
|
|
|
|
3 |
|
|
|
|||||
|
|
|
|
+ 5 ≥ 0, |
|
|
≥ −5, |
|||||||
Запишем ограничения: |
{ 2 − 6 + 45 ≥ 0. Отсюда: { (−∞; ∞). Возве- |
|||||||||||||
дём обе части уравнения в квадрат:
( + 5)2 = 49 ( 2 − 6 + 45).
Преобразуем:
9( + 5)2 = 4[( − 3)2 + 36], 4( − 3)2 − 9( + 5)2 = −4 ∙ 36,
( −3)36 2 − ( +5)16 2 = −1.
Полученное уравнение определяет гиперболу с центром в точке(3; −5) полуосями = 6, = 4. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет верхнюю ветвь гиперболы (рис. 3.23).
Пример. 3.6. Определить, какие из точек 1(5; −6), 2(−2; −4),
3(0; 3), 4(−√6; 0) лежат на гиперболе 8 2 − 5 2 = −48. Указание. Ес-
ли точка лежит на гиперболе, то её координаты удовлетворяют уравнению этой гиперболы.
145

|
|
|
|
|
|
|
|
|
|
|
−3 3 |
9 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
−1 |
|
|
|
|
|
|
|
|
|
|
−5 |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
−9 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
Рис. 3.23. Линия, заданная уравнением = −5 + |
√ |
2 |
− 6 + 45. |
|||||||
|
||||||||||
|
|
|
3 |
|
|
|
|
|||
(к Примеру 3.5 (7))
Решение.
Подставим координаты точки 1(5; −6) в левую часть уравнения гиперболы: 8 ∙ 52 − 5 ∙ (−6)2 = 200 − 180 = 20 ≠ −48, следовательно,
точка 1 не лежит на гиперболе.
Подставим координаты точки 2(−2; −4) в левую часть уравнения гиперболы: 8 ∙ (−2)2 − 5 ∙ (−4)2 = 32 − 80 = −48, следовательно, точка 2 лежит на гиперболе.
Подставим координаты точки 3(0; 3) в левую часть уравнения гиперболы: 8 ∙ 02 − 5 ∙ 32 = 0 − 45 = −45 ≠ −48, следовательно, точка 3 не лежит на гиперболе.
Подставим координаты точки 4(−√6; 0) в левую часть уравнения
гиперболы: 8 ∙ (−√6)2 − 5 ∙ 02 = 48 − 0 = 48 ≠ −48, следовательно, точка4 не лежит на гиперболе.
Ответ: точка 2 лежит на гиперболе.
Пример. 3.7. Найти точки пересечения прямой и гиперболы, если они заданы следующими уравнениями:
1)4 − 3 − 16 = 0, 252 − 162 = 1;
2)2 − + 1 = 0, 92 − 42 = 1;
3)2 − − 10 = 0, 202 − 52 = 1;
4)5 − 4 − 19 = 0, 8 2 − 3 2 − 48 − 6 + 16 = 0.
Решение.
Для нахождения координат точек пересечения прямой и гиперболы
нужно совместно решить их уравнения. |
|
|
|
|
||||||||||||
|
|
|
4 − 3 − 16 = 0, |
|
|
|
|
|||||||||
1) |
{ |
|
2 |
|
− |
2 |
= 1. |
|
|
|
|
|
||||
|
|
|
|
25 |
|
16 |
1 |
|
4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Выразим из первого уравнения : = |
(4 − 16) = |
|
( − 4) и под- |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
||||
ставим полученное выражение во второе уравнение: |
|
|||||||||||||||
|
2 |
|
− |
169 ( −4)2 |
|
= 1. |
|
|
|
|
|
|||||
25 |
|
16 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
146 |
|
|
|
|
|
|

Преобразуем:
2 |
− |
( −4)2 |
= 1, |
|
|
|
|||
25 |
|
9 |
|
|
9 2 |
− 25( − 4)2 = 225, |
|||
9 2 |
− 25( 2 − 8 + 16) = 225, |
|||
9 2 |
− 25 2 + 200 − 400 = 225, |
|||
−16 2 + 200 − 625 = 0, 16 2 − 200 + 625 = 0, (4 − 25)2 = 0.
Уравнение имеет два одинаковых действительных корня: = 254 . От-
сюда: = 43 (254 − 4) = 3.
Таким образом, прямая имеет одну точку пересечения с гиперболой,
то есть касается гиперболы в точке (254 ; 3).
2 − + 1 = 0,
2) { 92 − 42 = 1.
Выразим из первого уравнения : = 2 + 1 и подставим полученное выражение во второе уравнение:
2 − (2 +1)2 = 1
9 4
.
Преобразуем:
4 2 − 9(2 + 1)2 = 36, 4 2 − 9(4 2 + 4 + 1) = 36, 4 2 − 36 2 − 36 − 9 = 36, −32 2 − 36 − 45 = 0, 32 2 + 36 + 45 = 0.
Уравнение не имеет действительных корней, поэтому прямая не пе-
ресекает гиперболу.
2 − − 10 = 0,
3) { 202 − 52 = 1.
Выразим из первого уравнения : = 2 − 10 и подставим получен-
ное выражение во второе уравнение:
2 − (2 −10)2 = 1.
20 5
Преобразуем:
2 − 4(2 − 10)2 = 20,
2 − 4(4 2 − 40 + 100) = 20,
2 − 16 2 + 160 − 400 = 20,
−15 2 + 160 − 420 = 0, 3 2 − 32 + 84 = 0.
1 = 6, 2 = 143 .
Отсюда: 1 = 2 ∙ 6 − 10 = 2, 2 = 2 ∙ 143 − 10 = − 23 .
Таким образом, точки пересечения прямой с гиперболой: (6; 2),
(143 ; − 23).
147

5 − 4 − 19 = 0, 4) {8 2 − 3 2 − 48 − 6 + 16 = 0.
Выразим из первого уравнения : = 54 − 194 и подставим получен-
ное выражение во второе уравнение:
8 2 − 3 (54 − 194 )2 − 48 − 6 (54 − 194 ) + 16 = 0.
Преобразуем:
8 2 − 163 (5 − 19)2 − 48 − 64 (5 − 19) + 16 = 0, 128 2 − 3(5 − 19)2 − 768 − 24(5 − 19) + 256 = 0,
128 2 − 3(25 2 − 190 + 361) − 768 − 120 + 456 + 256 = 0, 128 2 − 75 2 + 570 − 1083 − 888 + 712 = 0, 53 2 − 318 − 371 = 0,2 − 6 − 7 = 0,
1 = −1, 2 = 7.
Отсюда: 1 = 54 ∙ (−1) − 194 = −6, 2 = 54 ∙ 7 − 194 = 4.
Таким образом, точки пересечения прямой с гиперболой: (−1; −6),
(7; 4).
Ответ: 1) (254 ; 3); 2) точек пересечения нет; 3) (6; 2), (143 ; − 23); 4) (−1; −6), (7; 4).
3.7. Эксцентриситет гиперболы
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к расстоянию между её вершинами. Эксцентриситет ги-
перболы, как и для эллипса, принято обозначать буквой . Можно записать:
= 22 = .
Таким образом, формула для нахождения эксцентриситета гипербо-
лы такая же как и для эллипса:
= .
При выводе канонического уравнения гиперболы было показано, что
> , поэтому > 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 + 2 |
= 2. Отсюда: |
|
|
|
|
|
|
|
|
|
|||||||||||
формула, связывающая , и : |
= √ |
2 + 2 |
. С |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
= √ |
2+ 2 |
= √1 + ( |
|
)2 . Возведём |
|||||||||||||||
учётом этого распишем : = |
|
= |
2+ 2 |
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
полученное равенство в квадрат: 2 = 1 + |
( |
|
)2. Выразим отсюда |
|
: ( |
|
)2 = |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 − 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= √ |
2 − 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При выводе канонического уравнения гиперболы была записана |
||||||||||||||||||||||||||||
Полученное равенство означает: чем ближе к 1, тем меньше |
|
и тем |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
больше вытянут основной прямоугольник. Таким образом, эксцентриситет характеризует форму основного прямоугольника и, следовательно, и самой гиперболы.
148

Если гипербола равносторонняя, то есть = , то = √1 + ( )2 =
= √1 + 1 = √2. Таким образом, эксцентриситет равносторонней гиперболы равен √2.
3.8. Фокальные радиусы гиперболы
При выводе канонического уравнения гиперболы было получено равенство
± √( − )2 + 2 = − 2.
Разделим это равенство на ± :
√( − )2 + 2 = ± ( − ).
Учитывая, что = , получаем:
√( − )2 + 2 = ±( − ).
Учитывая также, что √( − )2 + 2 = 2, получаем формулу для
нахождения фокального радиуса, проведённого из правого фокуса:
2 = ±( − ).
Воспользуемся равенством 1 − 2 = ±2 , где "+" относится к точ-
кам правой ветви гиперболы, "−" относится к точкам левой ветви гипербо-
лы. Получаем: 1 = 2 ± 2 = ±( − ) ± 2 = ±( + ).
Таким образом, формулы для нахождения фокальных радиусов точек правой ветви гиперболы:
= + , = − .
Формулы для нахождения фокальных радиусов точек левой ветви гиперболы:
= −( + ), = −( − ).
3.9. Директрисы гиперболы
Две прямые, перпендикулярные к той оси гиперболы, которая её пересекает, и расположенные симметрично относительно центра на расстоя-
нии от него, называются директрисами гиперболы.
Уравнения директрис имеют вид:
= ± .
Так как для гиперболы > 1, то < и, следовательно, левая дирек-
триса расположены между центром и левой вершиной, правая директриса расположены между центром и правой вершиной (рис. 3.24).
Рассмотрим величину , равную расстоянию от произвольной точки гиперболы до директрисы и рассмотрим фокальный радиус этой же точки, проведённый из ближайшего к директрисе фокуса. Связь между величинами , и эксцентриситетом выразим теоремой.
149
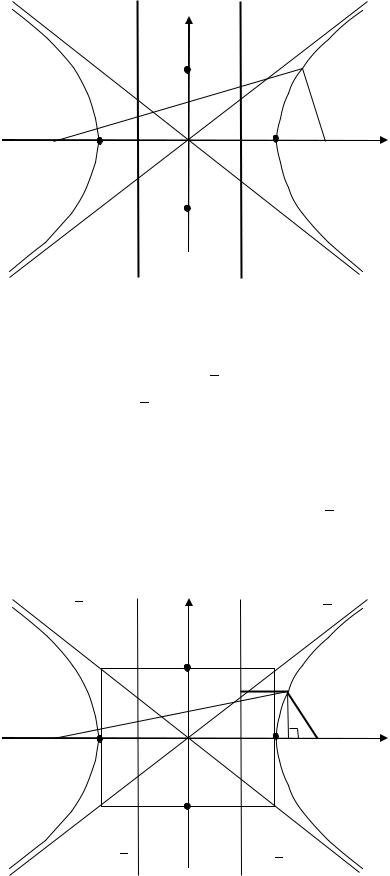
= − |
|
|
|
|
|
|
= |
|
|
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
||
1 |
|
− |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
= − |
|
|
|
= |
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
Рис. 3.24. Директрисы гиперболы
Теорема. Если – расстояние от произвольной точки гиперболы до какого-либо фокуса, – расстояние от этой же точки до соответствующей
этому фокусу директрисы, то отношение есть величина постоянная, рав-
ная эксцентриситету гиперболы: = .
Доказательство. Доказательство проведём для правого фокуса и правой директрисы. Пусть (; ) – произвольная точка гиперболы. Рассмотрим два случая.
1) Точка расположена на правой ветви гиперболы (рис. 3.25). По чертежу можно записать выражение для : = − . Далее запишем формулу для правого фокального радиуса: = − . Составляем искомое
отношение: |
|
= |
− |
= |
( − ) |
= . |
|
|
|
|
|||||
|
|
− |
|
|
− |
||
|
|
|
|
|
|
|
|
= − |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
− |
|
|
|
2 |
|
|
|
1 |
− |
|
|
|
= − |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.25. Доказательство связи , и для правой ветви гиперболы
150
