
821
.pdf
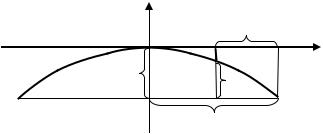
Выведем условие, при котором прямая = + касается параболы2 = 2. Если прямая касается параболы, то они имеют одну общую точку. Условие, при котором прямая касается параболы, можно получить, совместно решая уравнения прямой и параболы. При этом результатом совместного решения должна быть одна точка.
Составляем систему уравнений:
= + ,
{2 = 2 .
Подставим выражение для из первого уравнения во второе уравне-
ние:
( + )2 = 2.
Преобразуем:
2 2 + 2 + 2 − 2 = 0,
2 2 + (2 − 2) + 2 = 0,
2 2 + 2( − ) + 2 = 0,
Получили квадратное уравнение, которое имеет два одинаковых решения, то есть прямая и парабола имеют одну общую точку, если дискриминант уравнения равен нулю.
Найдём дискриминант полученного квадратного уравнения, когда коэффициент перед чётный (если квадратное уравнение записано в виде2 + + = 0, причём – чётное, то формула дискриминанта имеет вид
= (2)2 − ):
= ( − )2 − 2 2 = 2 2 − 2 + 2 − 2 2 = 2 − 2.
Приравняем дискриминант к нулю: 2 − 2 = 0. Преобразуем:
( − 2) = 0. Отсюда: = 2.
Таким образом, получено следующее условие, при котором прямая касается параболы:
= .
Уравнение касательной к параболе с вершиной в начале коорди-
нат.
Пусть точка 0( 0; 0) лежит на параболе 2 = 2. Через точку 0 проведём касательную к параболе. Касательную обозначим через
(рис. 3.24).
Уравнение касательной к параболе 2 = 2 в точке 0( 0; 0) име-
ет вид:
= ( + ).
Пример. 4.12. Составить уравнение касательной к параболе 2 = = 12 в её точке (3; −6).
Решение. По условию дана парабола с вершиной в начале координат, параметром = 6 и ветвями, направленными вправо. Точка (3; −6) лежит на этой параболе. Воспользуемся уравнением касательной к параболе в её точке 0( 0; 0) с вершиной в начале координат, параметром и ветвями,
211

|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
Рис. 3.24. Касательная к параболе 2 |
= 2 |
|
|
|||
направленными вправо: 0 = ( + 0). |
Подставляем: |
0 = 3, |
0 = −6, |
|||
= 6. Получаем: −6 = 6( + 3). Преобразуем: + + 3 = 0. |
|
|||||
Ответ: + + 3 = 0.
Пример 4.13. Составить уравнение прямой, которая касается параболы 2 = 8 и параллельна прямой 2 + 2 − 3 = 0.
Решение. Обозначим точку касания с параболой через 0. Пусть 0 – угловой коэффициент касательной. Парабола задана каноническим уравнением. Представим уравнение в виде 2 = 2 ∙ 4 ∙ . Отсюда параметр параболы = 4. Далее воспользуемся уравнением касательной к параболе в её точке 0( 0; 0): 0 = ( + 0). Подставим значение параметра в уравнение касательной: 0 = 4( + 0). Преобразуем уравнение касательной к
уравнению |
прямой с |
угловым коэффициентом = + . Получаем: |
||||||
= 4 + 4 , = |
4 |
+ |
4 0 |
. |
|
|
||
|
|
|
|
|||||
0 |
0 |
0 |
|
0 |
|
|
||
|
|
|
4 |
|
||||
Выпишем угловой коэффициент касательной: 0 = |
. |
|||||||
|
||||||||
|
|
|
|
|
|
0 |
||
Далее найдём угловой коэффициент данной прямой. Для этого преобразуем её уравнение к уравнению прямой с угловым коэффициентом: =
− + 32 . Выпишем угловой коэффициент данной прямой: = −1.
Так как касательная и данная прямая параллельны, то их угловые ко-
эффициенты равны, то есть 0 = . Получаем: 4 = −1. Отсюда 0 = −4.
0
Так как точка 0( 0; 0) лежит на параболе, то её координаты удовлетворяют уравнению параболы. Подставим координаты точки 0 с учётом того, что 0 = −4, в уравнение параболы: (−4)2 = 8 0. Отсюда 0 = 2. Получили точку касания 0(2; −4).
Подставим координаты точки касания в уравнение касательной:
−4 = 4( + 2).
Преобразуем: + + 2 = 0.
Ответ: + + 2 = 0.
Пример 4.14. Составить уравнения касательных к параболе 2 = = 36 , проведённых из точки (2; 9).
212
Решение. Обозначим точки касания с параболой через 1 и 2. Парабола задана каноническим уравнением. Представим уравнение в виде2 = 2 ∙ 18 ∙ . Отсюда параметр параболы = 18. Далее воспользуемся уравнением касательной к параболе в её точке 0( 0; 0): 0 = ( + 0). Подставим значение параметра в уравнение касательной: 0 = 18( + 0).
Так как точка (2; 9) лежит на касательной, то её координаты удовлетворяют уравнению касательной. В уравнение касательной вместо и
подставляем координаты точки : 9 0 = 18(2 + 0). Преобразуем: 0 = = 2(2 + 0).
Так как точка 0( 0; 0) лежит на параболе, то её координаты удовлетворяют уравнению параболы. Подставим координаты точки 0 в уравнение параболы: 02 = 36 0.
Составим систему полученных уравнений:
{ 0 =2 2(2 + 0),0 = 36 0.
Подставим во второе уравнение выражение для 0 из первого урав-
нения. Получаем:
[2(2 + 0)]2 = 36 0.
Преобразуем:
4(2 + 0)2 = 36 0, (2 + 0)2 = 9 0,02 − 5 0 + 4 = 0,
0(1) = 1, 0(2) = 4,
0(1) = 2(2 + 1) = 6, 0(2) = 2(2 + 4) = 12.
Получили две точки касания: 1(1; 6), 2(4; 12).
Подставляем координаты точек касания в уравнение касательной.
Подставляем координаты точки 1(1; 6):
6 = 18( + 1), 3 − + 3 = 0.
Подставляем координаты точки 2(4; 12):
12 = 18( + 4), 3 − 2 + 12 = 0. Ответ: 3 − + 3 = 0, 3 − 2 + 12 = 0.
Пример 4.15. Из точки (−3; 12) проведены касательные к параболе2 = 10 . Вычислить расстояние от точки до хорды, соединяющей точки касания.
Решение. Обозначим точки касания с параболой через 1 и 2. Парабола задана каноническим уравнением. Представим уравнение в виде2 = 2 ∙ 5 ∙ . Отсюда параметр параболы = 5. Далее воспользуемся уравнением касательной к параболе в её точке 0( 0; 0): 0 = ( + 0). Подставим значение параметра в уравнение касательной: 0 = 5( + 0).
Так как точка (−3; 12) лежит на касательной, то её координаты удовлетворяют уравнению касательной. В уравнение касательной вместо и подставляем координаты точки . Получаем: 12 0 = 5(−3 + 0).
Так как точка 0( 0; 0) лежит на параболе, то её координаты удовлетворяют уравнению параболы. Подставим координаты точки 0 в уравнение параболы: 02 = 10 0.
213

Составим систему полученных уравнений:
{ |
12 0 = 5(−3 + 0), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 = 10 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выразим из второго уравнения |
: = |
0 |
|
|
и подставим полученное |
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
10 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
выражение в первое уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12 |
= 5 (−3 |
+ |
|
0 |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12 |
= −15 + |
0 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 − 24 − 302 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(1) |
= 12 + √174 |
, (2) = 12 − √174 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= (12+√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(1) |
174) |
|
= 144+24√174+174 = 318+24√174 = 159+12√174 , |
|||||||||||||||||||||||||||||||||||
|
0 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
10 |
|
|
|
|
5 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(2) |
= 159−12√174 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получили две точки касания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
159+12√174 |
|
|
), ( |
159−12√174 |
|
|
|
||||||||||||||||||||||||||||||
( |
; 12 + √174 |
; 12 − √174). |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Составим уравнение хорды, соединяющей точки 1 и 2. Воспользуемся уравнением прямой с данным угловым коэффициентом и проходя-
щей через данную точку: |
|
− 0 |
|
= ( − 0). Найдём угловой коэффици- |
||||||||||||||||||||||||||||||||||||||||||||||||||
ент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2− 1 |
|
|
|
12−√174−(12+√174) |
|
|
12−√174−12−√174 |
|
−2√174 |
|
5 |
|
||||||||||||||||||||||||||||||||||||||||
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
. |
|||||||||||||||
|
|
159−12√ |
|
|
|
−159+12√ |
|
|
159−12√ |
174−159−12√ |
|
|
−24√ |
|
|
12 |
||||||||||||||||||||||||||||||||||||||
2− 1 |
174 |
174 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
174 |
174 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|
5 |
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Подставляем в уравнение прямой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
( − |
159+12√174 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
− (12 + √174) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
5 |
|
( − |
159 |
− |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
− 12 − √174 |
= |
|
√174), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
5 |
|
− |
159 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
− 12 − √174 |
= |
|
− √174, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
− |
5 |
− 12 + |
159 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
12 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
12 − 5 + 15 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5 − 12 − 15 = 0.
Получили уравнение хорды, соединяющей точки касания. Это уравнение представляет общее уравнение прямой.
Для вычисления расстояния от точки (−3; 12) до хорды применим
формулу расстояния от точки до прямой: = |
| 0+ 0+ | |
, где + + |
||||||||||||
|
√ |
|
|
|
|
|||||||||
|
2+ 2 |
|||||||||||||
+ = 0 – |
общее уравнение прямой; ( 0; 0) |
– точка, от которой находят |
||||||||||||
расстояние. |
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляем: |
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|5∙(−3)−12∙12−15| |
= |
|−15−144−15| |
= |
|−174| |
= |
174 |
. |
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
13 |
|
|
||||||
√52+(−12)2 |
|
13 |
13 |
|
|
|
||||||||
Ответ: 17413 .
214

4.7. Полярное уравнение параболы
Полярное уравнение параболы составляется аналогично полярному уравнению эллипса и имеет такой же вид. Учитывается, что для параболы
= 1.
Полярное уравнение параболы, когда направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс расположен в фокусе параболы, имеет вид:
= |
|
, |
|
||
− |
где – параметр параболы; и – полярные координаты.
Пример 4.16. Дано уравнение параболы 2 = 6. Составить её полярное уравнение, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в фокусе параболы.
Решение. Парабола задана каноническим уравнением. Представим уравнение в виде 2 = 2 ∙ 3 ∙ . Отсюда параметр параболы = 3. Полярное
уравнение параболы имеет вид = |
|
, |
где – параметр параболы. |
||||||||||||
|
|
|
|||||||||||||
1−cos |
|||||||||||||||
Подставляем: = |
3 |
|
|
. |
|
|
|
|
|
|
|
|
|||
1−cos |
|
|
|
|
|
|
|
|
|||||||
|
Ответ: = |
3 |
|
. |
|
|
|
|
|
|
|
|
|||
|
1−cos |
|
|
|
|
|
|
|
|
||||||
|
Пример 4.17. Найти параметр параболы, заданной полярным уравне- |
||||||||||||||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нием = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
6−6 cos |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Преобразуем полярное уравнение параболы к виду = |
||||||||||||||
|
|
|
|
7 |
|
|
7 |
|
|
|
7 |
|
|||
|
|
|
|
|
|
|
|
6 |
|
||||||
|
. Получаем: = |
|
|
|
= |
|
|
= |
|
. Отсюда параметр па- |
|||||
1−cos |
6−6 cos |
6(1−cos ) |
|
1−cos |
|||||||||||
раболы = 76 .
Ответ: 76 .
4.8. Парабола в прикладных задачах
Парабола находит широкое применение в различных областях техники, строительстве, астрономии, физике, оптике, повседневной жизни. Относительно параболы известны следующие факты.
1)Параболическую форму имеют зубья некоторых фрез (многозубый режущий инструмент), что даёт наибольшую прочность на изгиб, так как спинка зуба, выполненная в форме параболы, обеспечивает равнопрочность во всех сечениях по высоте зуба.
2)Кривая провисания проводов и тросов представляет цепную линию, которую при малых провисаниях заменяют параболой, что позволяет без существенных погрешностей упростить дальнейшие расчёты.
3)При строительстве зданий и сооружений используются параболические арки. Так в некоторых арочных мостах несущая конструкция пролётного строения выполняется по параболической кривой.
4)Траектория космического тела, двигающегося со скоростью, равной второй космической, представляет собой параболу. Такую скорость необходимо придать телу для преодоления притяжения Земли.
215
5) Если вращать параболу вокруг оси её симметрии, то получается поверхность, называемая параболоидом вращения. Форму параболоида имеет поверхность жидкости во вращающемся сосуде.
6)Если источник света находится в фокусе параболического зеркала, то лучи его, отразившись от зеркала, идут параллельно оси, на которой расположен фокус (оптическое свойство). Это свойство параболы применяют в устройстве фар и рефлекторов.
7)Камень, брошенный в пустоте, описывает параболическую траекто-
рию.
8)В парках культуры устраивается аттракцион, основанный на свойствах параболоида.
Задача 4.1. Арка железнодорожного моста, пролёт которой равен 60 м и высота равна 12 м, имеет форму параболы. Определить высоту боковых стоек арки, находящихся на расстоянии 15 м от его концов.
Решение. Примем за ось касательную к параболе в её вершине, за ось примем ось симметрии параболы (рис. 4.25).
15
|
|
2 |
|
|
12 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
30 |
|
|
|
|
|
Рис. 4.25. Параболическая арка моста (к Задаче 4.1 )
По условию пролёт арки равен 60 м, то есть расстояние между точками и равно 60 м и, следовательно, расстояние между точками и равно 30 м. По условию расстояние между точками и равно 12 м. Тогда точка имеет следующие координаты: (30; −12). Обозначим искомую высоту боковых стоек арки через 1. Обозначим через точку параболы, расположенную на расстоянии 15 м от концов моста. Обозначим через 2 расстояние от точки до оси . Тогда точка имеет следующие коорди-
наты: (15; − 2).
Воспользуемся каноническое уравнение параболы, симметричной относительно оси и расположенной в нижней полуплоскости: 2 = = −2 . Так как точка лежит на параболе, то её координаты удовлетво-
ряют уравнению параболы. Подставим координаты точки в уравнение параболы: 302 = −2 ∙ (−12). Отсюда параметр параболы = 37,5 и уравнение параболы принимает вид 2 = −75 . Так как точка лежит на параболе, то её координаты удовлетворяют уравнению параболы. Подставим координаты точки в уравнение параболы: 152 = −75 ∙ (− 2). Отсюда
2 = 3 и 1 = 12 − 2 = 12 − 3 = 9 м.
Ответ: 9 м.
Задача 4.2. Зеркальная поверхность прожектора образована вращением параболы вокруг её оси симметрии. Диаметр зеркала 80 см, а глубина 10 см. На каком расстоянии от вершины параболы нужно поместить источ-
216

ник света, если для отражения лучей параллельным пучком он должен быть в фокусе параболы?
Решение. Примем за ось касательную к параболе в её вершине, за ось примем ось симметрии параболы (рис. 4.26). По условию диаметр зеркала равен 80 см, то есть расстояние между точками и равно 80 см и, следовательно, расстояние между точками и равно 40 см. По условию расстояние между точками и равно 10 см. Тогда точка имеет следующие координаты: (40; 10). Обозначим искомый фокус параболы через .
|
|
|
|
|
|
|
|
40 |
|
|
|
|
10 |
|
|
|
|
Рис. 4.26. Поверхность прожектора, образованная вращением параболы вокруг её оси симметрии (к Задаче 4.2 )
Возьмём каноническое уравнение параболы, симметричной относительно оси и расположенной в верхней полуплоскости: 2 = 2. Так как точка лежит на параболе, то её координаты удовлетворяют уравнению параболы. Подставим координаты точки в уравнение параболы: 402 = 2 ∙ 10. Отсюда параметр параболы = 80 и фокус параболы(0; 40), то есть источник света надо поместить на расстоянии 40 см от вершины параболы.
Ответ: 40 см.
Задача 4.3. Из фокуса параболы 2 = 12 под острым углом к осинаправлен луч света. Известно, что = 34 . Дойдя до параболы, луч от
неё отразился. Составить уравнение прямой, на которой лежит отражённый луч. Указание. Если источник света находится в фокусе параболы, то лучи его, отразившись от параболы, идут параллельно оси, на которой расположен фокус.
Решение. Парабола задана каноническим уравнением. Представим уравнение в виде 2 = 2 ∙ 6 ∙ . Отсюда параметр параболы = 6 и фокус параболы (3; 0).
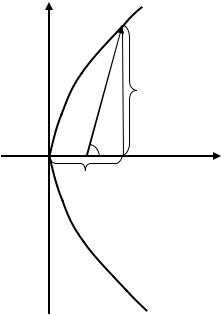
Обозначим через 0( 0; 0) точку пересечения луча с параболой |
|||||||||
(рис. 4.27). Из прямоугольного треугольника : = |
0 |
. По усло- |
|||||||
|
|||||||||
|
|
|
|
|
|
0 |
0−3 |
||
|
3 |
|
0 |
|
|
3 |
|
||
вию = |
. Тогда |
= |
. |
|
|
||||
|
−3 |
|
|
|
|||||
4 |
|
|
4 |
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
217 |
|
|
|
0 
0

|
|
|
|
|
0 |
Рис. 4.27. Луч, идущий из фокуса параболы и затем отражённый от параболы (к Задаче 4.3)
Так как точка 0 лежит на параболе, то её координаты удовлетворя-
ют уравнению параболы. Подставим координаты точки 0 в уравнение па- |
|||||||||||||||||||||||||||||
раболы: 2 = 12 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
Составим систему полученных уравнений: |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
= |
|
3 |
, |
|
|
|
|
|
|
|
|
|
|||||
|
{ 0−3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 = 12 . |
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
3 |
|
|
||||||||||||
|
Выразим из первого уравнения : |
= |
( − 3) и подставим полу- |
||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
4 |
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ченное выражение во второе уравнение: |
|
|
|
|
|
||||||||||||||||||||||||
[ |
3 |
|
( − 3)]2 = 12 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
4 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Преобразуем: |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
9 |
( − 3)2 = 12 , |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
16 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
( |
2 |
− 6 + 9) = 4 , |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
16 |
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
|
|
− 18 + 27 = 64 , |
|
|
|
|
|
|
|
||||||||||||||||||
0 |
2 |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
− 82 + 27 = 0, |
|
|
|
|
|
|
|
||||||||||||||||||
0 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= |
|
или = 27, |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
0 |
|
|
|
3 |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
3 |
|
( |
1 |
− 3) = −2 или = |
3 |
(27 − 3) = 18. |
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
0 |
|
|
|
4 |
3 |
|
|
|
|
0 |
4 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Точку |
( |
1 |
; −2) не рассматриваем, так как ей соответствует тупой |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||
угол, а по условию = |
, то есть угол острый. |
|
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||
Условию задачи соответствует одна точка 0(27; 18). Так как иско-
мая прямая проходит через точку 0 параллельно оси , то уравнение отражённого луча имеет вид − 18 = 0,
Ответ: − 18 = 0.
218

Задача 4.4. Струя воды фонтана достигает наибольшей высоты 4 м на расстоянии 0,5 м от вертикали, проходящей через точку выхода струи. Найти высоту струи над горизонталью на расстоянии 0,75 м от точки . Указание. Струя воды, выбрасываемая фонтаном, принимает форму параболы.
Решение. Возьмём каноническое уравнение параболы, симметричной относительно оси и расположенной в нижней полуплоскости: 2 = −2 (рис. 4.28).
|
|
|
−0,5 |
0,25 |
|
|
|
|
|
|
−4 |
|
Рис. 4.28. Струя воды фонтана, выходящая из точки (к Задаче 4.4)
С учётом исходных данных запишем координаты точки выхода струи: (−0,5; −4). Так как точка лежит на параболе, то её координаты удовлетворяют уравнению параболы. Подставим координаты точки в уравнение параболы: (−0,5)2 = −2 ∙ (−4). Отсюда параметр параболы
= 321 и уравнение параболы принимает вид 2 = − 161 .
Найдём ординату точки , расположенной на расстоянии 0,75 м от точки . Абсцисса точки равна 0,25. Подставляем это значение вместо
в уравнение параболы: 0,252 = − 161 . Отсюда = −1. Вычислим высоту
струи над горизонталью на расстоянии 0,75 м от точки : 4 − 1 = 3 м.
Ответ: 3 м.
Контрольные вопросы
1.Дайте определение параболы.
2.Запишите каноническое уравнение параболы в прямоугольной системе координат. Постройте параболу.
3.Запишите нормальное уравнение параболы в прямоугольной системе координат. Постройте параболу.
4.Дайте понятие фокуса параболы. Как его находят?
5.Дайте понятие директрисы параболы. Запишите её уравнение.
6.Запишите уравнение параболы в полярной системе координат.
219

Упражнения
1.Составить каноническое или нормальное уравнение параболы
свершиной в точке и параметром , если фокус параболы лежит на оси абсцисс (ординат) или на прямой, параллельной этой оси:
1)(0; 0), = 2. Ветви направлены вниз.
2)(0; 0), = 37 . Ветви направлены вправо.
3)(0; 0), = 12 . Ветви направлены влево.
4)(0; 0), = 4. Ветви направлены вверх.
5)(−5; −4), = 29 . Ветви направлены влево.
6)(3; 0), = 2. Ветви направлены вниз.
7)(0; −6), = 1. Ветви направлены вправо.
8)(− 75 ; 23), = 3. Ветви направлены вверх.
9)(3; 8), = 56 . Ветви направлены вниз.
10)(0; − 107 ), = 112 . Ветви направлены влево.
2.Определить координаты вершины , параметр и направление
ветвей параболы по её каноническому или нормальному уравнению:
1) 2 = 8 ; |
|
|
|
2) 2 = −9 ; |
|
|
|
|
|||||||
3) 2 = 10 ; |
|
|
|
4) 2 = − |
|
20 |
; |
|
|
|
|
||||
|
|
|
19 |
|
|
|
|
||||||||
5) ( + 3)2 = 4( − 5); |
|
6) ( + 6)2 = 12 ; |
|
|
|
||||||||||
7) ( − 1)2 = − ; |
|
|
8) 2 = |
16 |
|
( + 3); |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
5 |
2 |
|
|
|
|
2 |
|||
|
15 |
|
13 |
|
4 |
|
19 |
|
13 |
||||||
9) ( − |
|
) = 2 |
( + |
|
); |
10) ( − |
|
) |
= − |
|
( − |
|
) . |
||
4 |
7 |
|
18 |
10 |
|||||||||||
|
|
|
|
3 |
|
|
|
|
|
||||||
3.Построить параболу по её каноническому или нормальному
уравнению:
1) |
2 = 12 ; |
|
|
|
2) |
2 = −18 ; |
|
|
|
|
||||||
3) 2 = − ; |
|
|
|
4) 2 = 25 ; |
|
|
|
|
||||||||
5) |
( + 4)2 |
= −16 |
( + |
8 |
); |
6) |
2 = −8( − 1); |
|||||||||
|
||||||||||||||||
|
|
|
3 |
|
|
|
|
|
)2 |
|
|
|
|
|
||
7) |
( + 3)2 |
= 7 ; |
|
|
|
8) |
( − |
90 |
= |
100 |
( − |
5 |
); |
|||
|
|
|
|
|
41 |
|
||||||||||
|
|
|
|
|
|
|
17 |
|
)2 |
|
2 |
|||||
9) |
( − 5)2 |
= − 3; |
10) ( + |
5 |
= . |
|
|
|
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
4. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
1)парабола расположена в левой полуплоскости симметрично относительно оси и её параметр = 0,5;
2)парабола расположена в верхней полуплоскости симметрично от-
носительно оси и её параметр = 14 ;
3)парабола расположена симметрично относительно оси и проходит через точку (−1; 3);
4)парабола расположена симметрично относительно оси и проходит через точку (1; 1);
5)фокус параболы (−7; 0) и уравнение директрисы − 7 = 0.
220
