
821
.pdf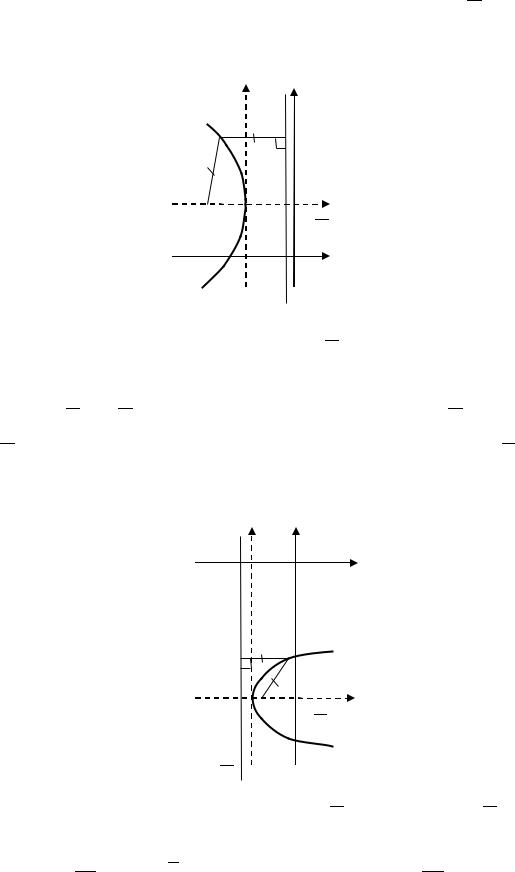
= −2 ∙ 5 ∙ ( − (−3)). Вершина параболы находится в точке (−3; 215 ), вет-
ви направлены влево, параметр = 5, фокус (− |
11 |
; |
21 |
), директриса = |
|||
|
|
||||||
|
1 |
|
2 |
5 |
|
||
− |
(рис. 4.14). |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
− |
21 ′ |
|
|
||||
|
|
5 |
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
= − |
1 |
|
|
|
|
||
|
|
|
2 |
|
Рис. 4.14. Парабола с вершиной в точке (−3; 215 ) и параметром = 5 (к Примеру 4.3 (8))
9)( + 193 )2 = 3619 ( + 2). Преобразуем уравнение: ( − (− 193 ))2 =
=2 ∙ 1819 ∙ ( − (−2)). Вершина параболы находится в точке (−2; − 193 ),
ветви направлены вправо, параметр = |
18 |
, фокус (− |
29 |
; − |
19 |
), директри- |
|||
|
|
|
|||||||
|
47 |
19 |
|
19 |
3 |
|
|||
са = − |
(рис. 4.15). |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
19 |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
||
|
|
−2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
− |
19 |
|
′ |
|
|
3 |
|
= − 4719
Рис. 4.15. Парабола с вершиной в точке (−2; − 193 ) и параметром = 1819 (к Примеру 4.3 (9))
10) ( − 10031 )2 = −5√5 . Преобразуем уравнение: ( − 10031 )2 =
201

= −2 ∙ 5√25 ∙ ( − 0). Вершина параболы находится в точке (0; 10031 ), ветви
направлены влево, параметр = 5√25 , фокус (− 5√45 ; 10031 ), директриса =
5√45 (рис. 4.16).
, ′
100 ′
3
= 5√54
Рис. 4.16. Парабола с вершиной в точке (0; 10031 ) и параметром = 5√25 (к Примеру 4.3 (10))
Пример 4.4. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
1)парабола расположена в правой полуплоскости симметрично относительно оси и её параметр = 3;
2)парабола расположена в нижней полуплоскости симметрично от-
носительно оси и её параметр = 3;
3)парабола расположена симметрично относительно оси и проходит через точку (9; 6);
4)парабола расположена симметрично относительно оси и проходит через точку (4; −8);
5)фокус параболы (0; −3) и осью параболы служит ось .
Решение.
1)Каноническое уравнение параболы имеет вид 2 = 2 . Подстав-
ляем = 3: 2 = 6 .
2)Каноническое уравнение параболы имеет вид 2 = −2 . Подставляем = 3: 2 = −6 .
3)Каноническое уравнение параболы имеет вид 2 = 2 . Подставляем координаты точки : 62 = 2 ∙ 9. Отсюда параметр параболы = 2 и уравнение параболы 2 = 4 .
4)Каноническое уравнение параболы имеет вид 2 = −2 . Подставляем координаты точки : 42 = −2 ∙ (−8). Отсюда параметр параболы
= 1 и уравнение параболы 2 = −2 .
5)Каноническое уравнение параболы имеет вид 2 = −2 . Расстоя-
ние от вершины параболы до фокуса равно 3, поэтому 2 = 3 и = 6. Уравнение параболы 2 = −12 .
202

Ответ: 1) 2 = 6 ; 2) 2 = −6 ; 3) 2 = 4 ; 4) 2 = −2 ; 5) 2 = = −12 .
Пример 4.5. Среди приведённых уравнений указать уравнения пара-
болы, найти параметр каждой из них: |
|
|
|
|
|
||||
1) 5 − 2 = 0; |
2) 2 = 4 ; |
||||||||
3) |
2 |
+ |
2 |
= 1; |
4) 2 2 + 7 2 = 1; |
||||
|
|
||||||||
144 |
25 |
|
|
|
|
|
|
||
5) 2 |
= − ; |
6) 2 = −3 ; |
|||||||
7) 2 + 2 = 2; |
8) 2 = |
1 |
|
; |
|||||
|
|||||||||
|
2 |
|
2 |
|
2 |
|
|
|
|
9) |
− |
= 1; |
10) 2 = |
|
8 |
. |
|||
|
|
|
|||||||
100 |
36 |
|
|
|
3 |
||||
Решение.
1) 5 − 2 = 0. Сравнивая данное уравнение с каноническими уравнениями параболы 2 = 2 , 2 = −2 , 2 = 2 , 2 = −2 , устанавливаем, что данное уравнение не определяет параболу, так как не содержит квадраты переменных. Оно представляет прямую, параллельную оси и
отсекающей на оси отрезок = 25 .
2)2 = 4 . Запишем уравнение в виде 2 = 2 ∙ 2 ∙ . Сравнивая данное уравнение с каноническим уравнением параболы 2 = 2 , устанавливаем, что данное уравнение определяет параболу с параметром = 2.
3)1442 + 252 = 1. Сравнивая данное уравнение с каноническими урав-
нениями параболы 2 = 2 , 2 = −2 , 2 = 2 , 2 = −2 , устанавливаем, что данное уравнение не определяет параболу, так как содержит квадраты обеих переменных. Оно определяет эллипс.
4) 2 2 + 7 2 = 1. Сравнивая данное уравнение с каноническими уравнениями параболы 2 = 2 , 2 = −2 , 2 = 2 , 2 = −2 , устанавливаем, что данное уравнение не определяет параболу, так как содержит квадраты обеих переменных. Оно определяет эллипс.
5)2 = − . Запишем уравнение в виде 2 = −2 ∙ 12 ∙ . Сравнивая данное уравнение с каноническим уравнением параболы 2 = −2 , устанавливаем, что данное уравнение определяет параболу с параметром = 12 .
6)2 = −3 . Запишем уравнение в виде 2 = −2 ∙ 32 ∙ . Сравнивая данное уравнение с каноническим уравнением параболы 2 = −2 , устанавливаем, что данное уравнение определяет параболу с параметром = 32 .
7)2 + 2 = 2. Сравнивая данное уравнение с каноническими уравнениями параболы 2 = 2 , 2 = −2 , 2 = 2 , 2 = −2 , устанавли-
ваем, что данное уравнение не определяет параболу, так как содержит квадраты обеих переменных. Оно определяет окружность.
8) 2 = 12 . Запишем уравнение в виде 2 = 2 ∙ 14 ∙ . Сравнивая данное уравнение с каноническим уравнением параболы 2 = 2 , устанавливаем, что данное уравнение определяет параболу с параметром = 14 .
203

9) 1002 − 362 = 1. Сравнивая данное уравнение с каноническими урав-
нениями параболы 2 = 2 , 2 = −2 , 2 = 2 , 2 = −2 , устанавливаем, что данное уравнение не определяет параболу, так как содержит квадраты обеих переменных. Оно определяет гиперболу.
10) 2 = 83 . Запишем уравнение в виде 2 = 2 ∙ 43 ∙ . Сравнивая данное уравнение с каноническим уравнением параболы 2 = 2 , устанавливаем, что данное уравнение определяет параболу с параметром = 43 .
Ответ: 2), = 2; 5), = 12 ; 6), = 32 ; 8), = 14 ; 10), = 43 .
Пример 4.6. Установить, какие линии определяются следующими
уравнениями: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) = 2√ |
|
; |
|
|
|
|
|
2) = −3√−2 ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) = −5√− ; |
4) = √5 ; |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
5) = −8 + √10 ; |
6) = 3 − √−22 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
7) = 4 + √−6 − 12. |
|
|
|
|
|
|
|
||||||||
Решение. |
|
|
|
|
|
|
|
||||||||
1) = 2√ . Запишем ограничения: { ≥ 0, Возведём обе части урав-
≥ 0.
нения в квадрат: 2 = 4 . Преобразуем: 2 = 2 ∙ 2 ∙ . Полученное уравнение определяет параболу. Вершина параболы находится в точке (0; 0), ветви направлены вправо, параметр = 2, фокус (1; 0), директриса = −1. Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет часть параболы, расположенную в первом координатном углу (рис. 4.17).
|
|
|
|
|
|
|
|
= −1 |
|
|
|
Рис. 4.17. Парабола с вершиной в точке (0; 0) и параметром = 1 |
|||||
|
|
(к Примеру 4.6 (1)) |
|
|
|
|
|
|
|
≤ 0, |
≤ 0, |
|
|
|
|
||
2) = −3√−2 . Запишем ограничения: {−2 ≥ 0. |
Отсюда: { ≤ 0. |
||||
Возведём обе части уравнения в квадрат: 2 |
= −18 . Преобразуем: 2 = |
||||
−2 ∙ 9 ∙ . Полученное уравнение определяет параболу. Вершина параболы находится в точке (0; 0), ветви направлены влево, параметр = 9, фокус
(− 29 ; 0), директриса = 29 . Учитывая полученные выше ограничения, за-
204

ключаем, что исходное уравнение определяет часть параболы, расположенную в третьем координатном углу (рис. 4.18).
|
= |
9 |
|
2 |
|
|
|
Рис. 4.18. Парабола с вершиной в точке (0; 0) и параметром = 29 (к Примеру 4.6 (2))
|
|
|
{ |
≤ 0, |
|
{ ≤ 0, |
3) = −5√− . Запишем ограничения: |
Отсюда: |
|||||
|
|
|
|
− ≥ 0. |
|
≤ 0. |
Возведём обе части уравнения в квадрат: 2 = −25 . Преобразуем: 2 =
−2 ∙ 252 ∙ . Полученное уравнение определяет параболу. Вершина параболы находится в точке (0; 0), ветви направлены вниз, параметр = 252 , фокус
(0; − 254 ), директриса = 254 . Учитывая полученные выше ограничения,
заключаем, что исходное уравнение определяет часть параболы, расположенную в третьем координатном углу (рис. 4.19).
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.19. Парабола с вершиной в точке (0; 0) и параметром = |
25 |
|
|
|
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
(к Примеру 4.6 (3)) |
|
|
|
|
|
|
|
|
|
|
≥ 0, |
|
|
≥ 0, |
|
|
|
||
|
|
|
|
|
|
|
||||
4) = √5 . Запишем ограничения: {5 ≥ 0. |
Отсюда: { ≥ 0. |
Возве- |
||||||||
дём обе части уравнения в квадрат: 2 = 5 . Преобразуем: |
2 = 2 ∙ |
5 |
∙ . |
|||||||
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
Полученное уравнение определяет параболу. Вершина параболы находится в точке (0; 0), ветви направлены вверх, параметр = 52 , фокус (0; 54),
директриса = − 54 . Учитывая полученные выше ограничения, заключаем,
что исходное уравнение определяет часть параболы, расположенную в первом координатном углу (рис. 4.20).
205

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||
Рис. 4.20. Парабола с вершиной в точке (0; 0) и параметром = |
5 |
|
|
||||||||
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
(к Примеру 4.6 (4)) |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
5) = −8 + √10 . Перепишем уравнение в виде: + 8 = √10 . За- |
|||||||||||
пишем ограничения: |
{ + 8 ≥ 0, |
Отсюда: |
{ ≥ −8, |
Возведём обе части |
|||||||
|
|
10 ≥ 0. |
|
≥ 0. |
|
|
|
|
|
||
уравнения в квадрат: ( + 8)2 = 10 . Преобразуем: ( − (−8))2 =
=2 ∙ 5( − 0). Полученное уравнение определяет параболу. Вершина параболы находится в точке (0; −8), ветви направлены вправо, параметр =
=5, фокус (52 ; −8), директриса = − 52 . Учитывая полученные выше
ограничения, заключаем, что исходное уравнение определяет часть параболы, расположенной выше прямой = −8 (рис. 4.21).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −8 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
= − |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|||
Рис. 4.21. Парабола с вершиной в точке (0; −8) и параметром = 5 |
||||||||
|
|
(к Примеру 4.6 (5)) |
|
|
|
|||
|
|
|
|
|
|
|
||
6) = 3 − √−22 . Перепишем уравнение в виде: − 3 = −√−22 . |
||||||||
|
|
− 3 ≤ 0, |
≤ 3, |
|
|
|
||
Запишем ограничения: {−22 ≥ 0. Отсюда: |
{ ≤ 0. |
Возведём обе части |
||||||
уравнения в квадрат: ( − 3)2 = −22 . Преобразуем: ( − 3)2 = −2 ∙ 11 . Полученное уравнение определяет параболу. Вершина параболы находится
в точке (3; 0), ветви направлены вниз, параметр = 11, фокус (3; − 112 ),
директриса = 112 . Учитывая полученные выше ограничения, заключаем, что исходное уравнение определяет часть параболы, расположенной левее прямой = 3 (рис. 4.22).
206

|
|
|
|
|
|
|
= |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 |
|
|
||||
|
Рис. 4.22. Парабола с вершиной в точке (3; 0) и параметром = 11 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
(к Примеру 4.6 (6)) |
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
7) = 4 + √−6 − 12. Перепишем уравнение в виде: − 4 = |
|
|||||||||
|
|
|
|
− 4 ≥ 0, |
|
≥ 4, |
|||||
= √−6( + 2). Запишем ограничения: { |
|
Отсюда: { |
|||||||||
|
|
|
|
|
|
−6( + 2) ≥ 0. |
|
≤ −2. |
|||
Возведём обе части уравнения в квадрат: ( − 4)2 = −6( + 2). Преобразуем: ( − 4)2 = −2 ∙ 3( − (−2)). Полученное уравнение определяет параболу. Вершина параболы находится в точке (−2; 4), ветви направлены
влево, параметр = 3, фокус (− 72 ; 4), директриса = − 12 . Учитывая
полученные выше ограничения, заключаем, что исходное уравнение определяет часть параболы, расположенной выше прямой = 4 (рис. 4.23).
= 4
|
|
|
|
= −2 |
= − |
1 |
|
|
|
||
|
2 |
|
|
Рис. 4.23. Парабола с вершиной в точке (−2; 4) и параметром = 3 (к Примеру 4.6 (7))
Пример 4.7. Составить уравнение параболы, вершина которой находится в начале координат, зная, что фокус параболы (49 ; 0) и уравнение
директрисы 4 + 9 = 0.
Решение. Фокус расположен на положительной части оси на рас-
стоянии 49 от начала координат. Директриса пересекает отрицательную
часть оси , параллельна оси и расположена на таком же расстоянии от начала координат, что и фокус. Поэтому ветви параболы направлены
207

вправо, её уравнение имеет вид 2 = 2 , где 2 = 49 , = 29 . Составляем
уравнение параболы: 2 = 2 ∙ 29 ∙ = 9 .
Ответ: 2 = 9 .
Пример. 4.8. Определить, какие из точек 1(−2; 4), 2(−2; 3),
3(1; −√2), 4(−1; 2√2) лежат на параболе 2 = −8 . Указание. Если точ-
ка лежит на параболе, то её координаты удовлетворяют уравнению этой параболы.
Решение.
Подставим координаты точки 1(−2; 4) в уравнение параболы: 42 = −8 ∙ (−2). Отсюда 16 = 16, следовательно, точка 1 лежит на параболе.
Подставим координаты точки 2(−2; 3) в уравнение параболы: 32 = −8 ∙ (−2). Отсюда 9 ≠ 16, следовательно, точка 2 не лежит на параболе.
Подставим координаты точки 3(1; −√2) в уравнение параболы:
(−√2)2 = −8 ∙ 1. Отсюда 2 ≠ −8, следовательно, точка 3 не лежит на параболе.
Подставим координаты точки 4(−1; 2√2) в уравнение параболы:
(2√2)2 = −8 ∙ (−1). Отсюда 8 = 8, следовательно, точка 4 лежит на параболе.
Ответ: точки 1 и 4 лежат на параболе.
Пример 4.9. Вычислить фокальный радиус точки параболы 2 = 20 , если абсцисса точки равна 7.
Решение. Обозначим ординату точки через 0. Тогда (7; 0). Преобразуем уравнение параболы: 2 = 2 ∙ 10 ∙ . Параметр параболы = 10, фокус (5; 0). Найдём 0. Для этого подставим координаты точки в уравнение параболы: 02 = 20 ∙ 7, 0 = ±√140. Получаем две точки:
1(7; √140), 2(7; −√140).
Вычислим фокальный радиус точки , то есть расстояние = 1 или = 2. Получаем:
= 1 = √(5 − 7)2 + (0 − √140)2 = √4 + 140 = 12.
Ответ: 12.
Пример 4.10. Установить, что каждое из следующих уравнений определяет параболу, найти координаты её вершины и величину параметра:
1) = |
1 |
2 |
+ + 2; |
2) = 2 2 − 12 + 14; |
3) = − 2 + 2 − 1. |
|
|||||
4 |
|
|
|
|
|
Решение.
1) = 14 2 + + 2. Выделим полный квадрат в правой части уравнения. Для этого применим формулу сокращённого умножения: 2 + 2 +
+ 2 = ( + )2. Получаем: = 14 2 + + 2 = 14 ( 2 + 4 + 8) = = 14 [( 2 + 2 ∙ 2 ∙ + 4) + 4] = 14 [( + 2)2 + 4] = 14 ( + 2)2 + 1.
Запишем уравнение в виде: − 1 = 14 ( + 2)2, ( − (−2))2 = = 4( − 1).
208

Далее применим формулы преобразования координат при параллель-
ном сдвиге осей: { ′ = − 0, Здесь ( ; ) – новое начало координат;′ = − 0.
– старая система координат, ′ ′ – новая система координат; , – старые
координаты; ′, ′ – новые координаты. |
|
||
В примере обозначим − 1 через ′, |
− (−2) через ′. Получаем |
||
следующие формулы: { |
′ = − (−2), |
Подставим эти формулы в преобра- |
|
′ = − 1. |
|||
зованное уравнение. Получаем: ′2 = 4 ′. Это каноническое уравнение параболы. Вершина такой параболы находится в точке (−2; 1), параметр
= 2.
2) = 2 2 − 12 + 14. Выделим полный квадрат в правой части
уравнения. Для этого применим формулу сокращённого умножения: 2 −
2 + 2 = ( − )2. Получаем: = 2 2 − 12 + 14 =
=2( 2 − 6 + 7) = 2[( 2 − 2 ∙ 3 ∙ + 9) − 2] = 2[( − 3)2 − 2] =
=2( − 3)2 − 4.
Запишем уравнение в виде:
+ 4 = 2( − 3)2, ( − 3)2 = 12 ( − (−4)).
Далее применим формулы преобразования координат при параллель-
ном сдвиге осей: { ′ = − 0, Здесь ( ; ) – новое начало координат;′ = − 0.
– старая система координат, ′ ′ – новая система координат; , – старые
координаты; ′, ′ – новые координаты. |
|
||||
В примере обозначим − (−4) через ′, − 3 через ′. |
Получаем |
||||
следующие формулы: { |
′ = − (−4), |
Подставим эти формулы в преобра- |
|||
′ = − 3. |
|||||
зованное уравнение. Получаем: ′2 = |
1 |
′. Это каноническое уравнение па- |
|||
2 |
|||||
|
|
|
|
||
раболы. Вершина такой параболы находится в точке (−4; 3), |
параметр |
||||
= 14 .
3)= − 2 + 2 − 1. Выделим полный квадрат в правой части урав-
нения. Для этого применим формулу сокращённого умножения: 2 − 2 + + 2 = ( − )2. Получаем: = − 2 + 2 − 1 = −( 2 − 2 + 1) =
= −( − 1)2.
Запишем уравнение в виде: ( − 1)2 = −( − 0).
Далее применим формулы преобразования координат при параллель-
ном сдвиге осей: { ′ = − 0, Здесь ( ; ) – новое начало координат;′ = − 0.
– старая система координат, ′ ′ – новая система координат; , – старые координаты; ′, ′ – новые координаты.
В примере обозначим − 0 через ′, − 1 через ′. Получаем сле-
дующие формулы: { ′ = − 0, Подставим эти формулы в преобразованное
′ = − 1.
209

уравнение. Получаем: ′2 = − ′. Это каноническое уравнение параболы. Вершина такой параболы находится в точке (0; 1), параметр = 12 .
Ответ: 1) (−2; 1), = 2; 2) (−4; 3), = 14 ; 3) (0; 1), = 12 .
Пример 4.11. Найти точки пересечения прямой и параболы, если они заданы следующими уравнениями:
1)− + 2 = 0, 2 = 8 ;
2)8 + 3 − 15 = 0, 2 = −3 ;
3)5 − − 15 = 0, 2 = −5 .
Решение. Для нахождения координат точек пересечения прямой и параболы нужно совместно решить их уравнения.
1) |
{ − + 2 = 0, |
|
2 = 8 . |
Выразим из первого уравнения : = − 2 и подставим полученное выражение во второе уравнение: 2 = 8( − 2). Преобразуем: 2 − 8 + +16 = 0, ( − 4)2 = 0. Уравнение имеет два одинаковых действительных корня: = 4. Отсюда: = 4 − 2 = 2. Таким образом, прямая имеет одну точку пересечения с параболой, то есть касается параболы в точке (2; 4).
2) {8 + 3 − 15 = 0, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 = −3 . |
|
|
|
|
|
|
|
|
|
|
|||||||
Выразим из первого уравнения : = − |
8 |
+ 5 и подставим полу- |
||||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
ченное выражение во второе уравнение: 2 |
= −3 (− |
8 |
+ 5). Преобразуем: |
|||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
8 |
|
||||
2 = 8 − 15, 2 − 8 + 15 = 0, |
= 3, |
= 5. Отсюда: = − |
∙ 3 + 5 = |
|||||||||||||||
|
||||||||||||||||||
|
|
|
1 |
2 |
|
|
1 |
3 |
||||||||||
|
|
8 |
|
|
25 |
|
|
|
|
|
|
|
|
|
||||
= −3, = − |
∙ 5 + 5 = − |
. Таким образом, |
точки пересечения прямой с |
|||||||||||||||
|
|
|
||||||||||||||||
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
параболой: (3; −3), (5; − |
25 |
). |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) {5 − − 15 = 0, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 = −5 . |
|
|
|
|
|
|
|
|
|
|
|||||||
Выразим из первого уравнения : = |
1 |
+ 3 и подставим получен- |
||||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||
ное выражение во второе уравнение: 2 = −5 (15 + 3). Преобразуем: 2 =
− − 15, 2 + + 15 = 0. Уравнение не имеет действительных корней, поэтому прямая не пересекает параболу.
Ответ: 1) (2; 4); 2) (3; −3), (5; − 253 ); 3) точек пересечения нет.
4.6. Касательная к параболе
В ряде задач аналитической геометрии, связанных с параболой, требуется использовать условие, при котором прямая касается параболы, а также составлять уравнения касательных к параболе.
Условие, при котором прямая касается параболы с вершиной в начале координат.
210
