
Динамический хаос (ИПИС, ФКС)
.pdf
5) Связь и коммуникации.
Одно из возможных приложений хаоса состоит в использовании генерируемых динамическими системами хаотических сигналов в целях коммуникации. Благодаря хаотической природе сигналов открываются новые возможности для кодирования информации, которая становится труднодоступной для перехвата. К настоящему моменту уже предложен целый ряд схем, обеспечивающих связь на хаотических сигналах.
6) Сжатие, хранение и обработка информации. Открываются новые возможности для сжатия, хранения и обработки информации. В частности, разработаны методы сжатия информации на основе идей фрактальной геометрии. Разрабатываются варианты реализации вычислительных процессов в системах, отличных от традиционной компьютерной архитектуры и опирающихся на явления нелинейной динамики.

Хаос в простых моделях динамических систем
Как говорилось ранее, состояние динамической системы в некоторый момент времени можно задать с помощью набора её динамических переменных. Так для бильярдного шара такими переменными являются x, y, vx и vy .
Совокупность этих динамических переменных образует фазовое пространство системы, в котором состояние системы можно отобразить в виде точки x (x, y, vx , vy ). При изменении же состояния системы с течением времени точка будет перемещаться в фазовом пространстве по некоторой линии – фазовой траектории. В общем случае, если состояние системы задаётся N динамическими переменными, то динамику системы можно представить как
движение точки по фазовой траектории в |
N -мерном |
фазовом пространстве. |
|

Выделяют два класса динамических систем – консервативные и диссипативные.
В физике к консервативным относятся, например, механические колебательные системы, в которых отсутствует трение. В таких консервативных системах энергия сохраняется. В присутствии же трения механическая энергия не сохраняется, а постепенно рассеивается (диссипирует) и переходит в тепло. Такие системы относят к диссипативным.
Однако, как было сказано ранее, под динамическими системами можно понимать не только механические системы, но и системы другой природы. В связи с этим понятия консервативность и диссипативность могут быть обобщены на случай произвольной динамической системы.

Пусть мы имеем некоторую динамическую систему, т.е. задано фазовое пространство и указан оператор эволюции. Вместо одной системы рассмотрим ансамбль, состоящий из большого количества её идентичных копий, причём все системы в ансамбле могут отличаться друг от друга только лишь начальными условиями. В фазовом пространстве такой ансамбль представляется облаком изображающих точек. С течением времени изображающие точки будут перемещаться в фазовом пространстве в соответствии с динамическими уравнениями системы, так что форма облака и его размеры могут измениться.
Может случиться так, что объём облака в процессе временной эволюции будет оставаться постоянным. Это характерно для консервативных систем, к которым, в частности, относятся и гамильтоновы системы, рассматриваемые в классической механике.
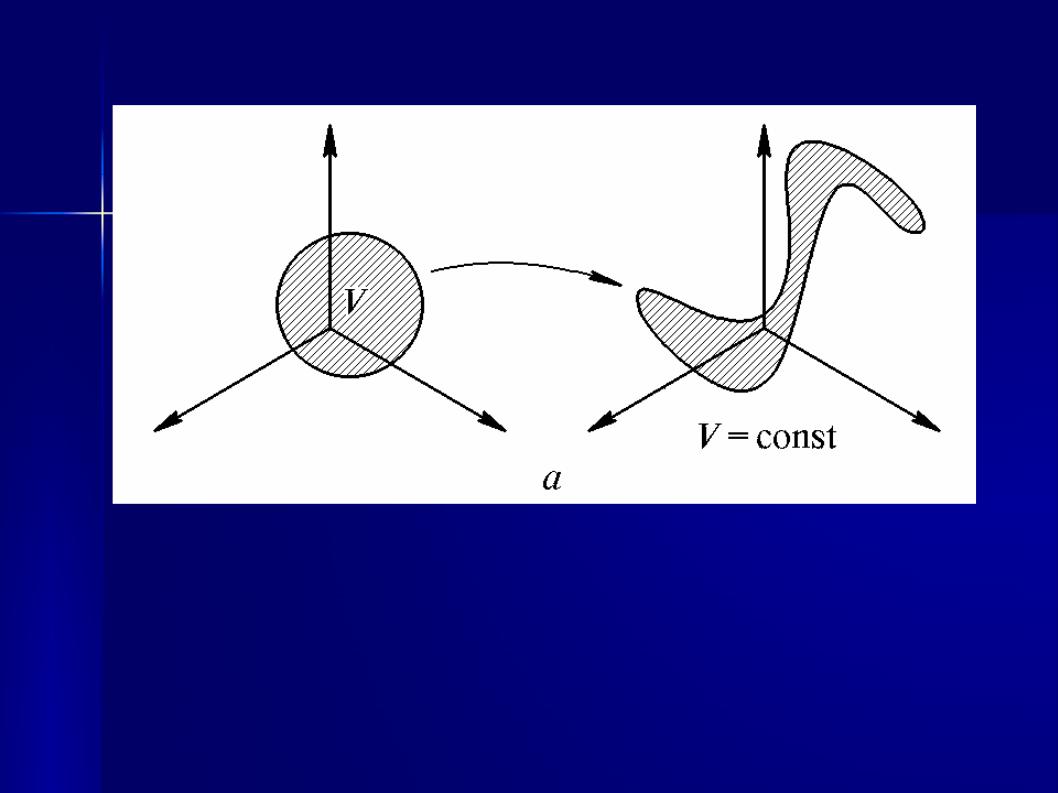
Рис. 3 а. Консервативные динамические системы.

Если же рассматриваемая система диссипативная, то с течением времени облако изображающих точек «съёживается» и концентрируется в итоге на одном или нескольких аттракторах
Рис. 3 б. Диссипативные динамические системы.

Под аттрактором (англ. attract – привлекать, притягивать) понимают множество точек в фазовом пространстве, посещаемых диссипативной системой в установленном режиме. Примеры аттракторов – устойчивое состояние равновесия, предельный цикл, отвечающий режиму периодических автоколебаний и т.д..

Рис. 4. Фазовые траектории затухающих колебаний, происходящих по закону x Aexp( t)cos( t ).

Для диссипативных систем характерно то, что режим динамики, возникающий в системе, предоставленной себе в течение длительного времени, становится не зависящим от начального состояния (по крайней мере при изменении начальных условий в некоторых конечных пределах).
Рис. 5. Фазовые траектории автоколебательных систем.

При наличии в фазовом пространстве двух или более аттракторов говорят, что имеет место, соответственно, бистабильность и мультистабильность. Множество точек базового пространства, из которых траектории приходят в конце-концов к какому-то одному аттрактору, называется бассейном этого аттрактора.
Рис. 6. Фазовый портрет системы с несколькими аттракторами.
