Лекция 11

_{Примеры построения эпюр М и Q в изгибаемых балках.}

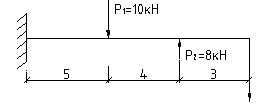
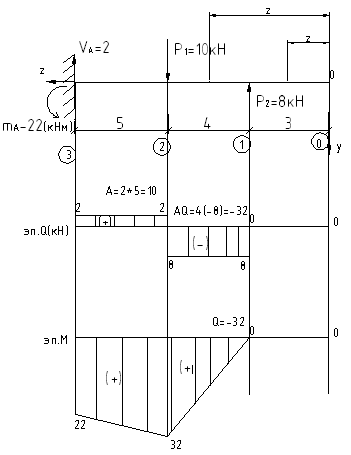
1. _Уч.0-1,

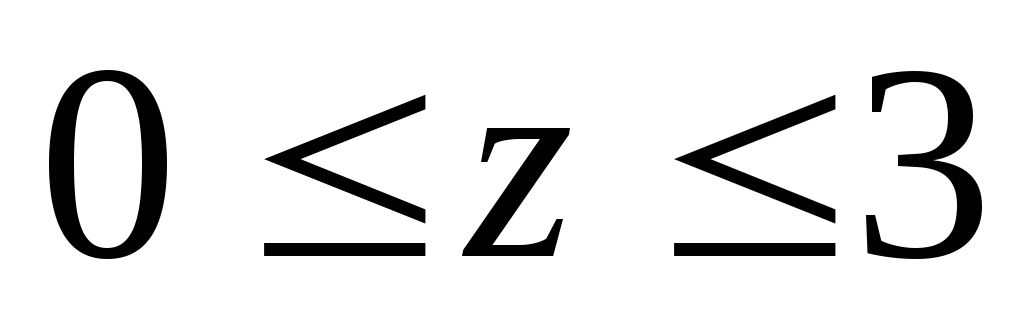
_РОЗУ

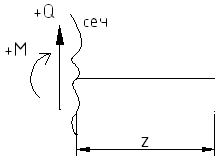
_Q=?

_{-Q=0, Q=0- на незагруженном конце балки Q=0}

_{: -М=0, М=0 - на свободном незагруженном конце балки моментов = 0: М=0.}

_Уч.1-2,

_РОЗУ

_:

_:

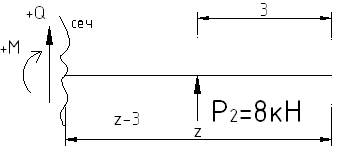
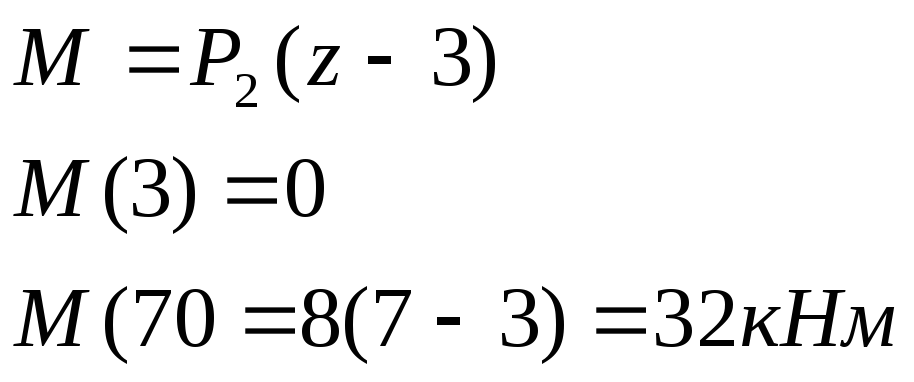
_Уч.2-3,

_РОЗУ

_:

_:

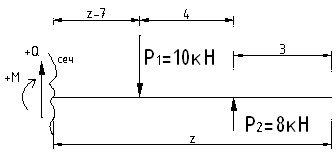
_{Значения VA и mA найдены из эпюр.}

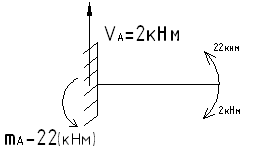
2. _Уч.0-1,

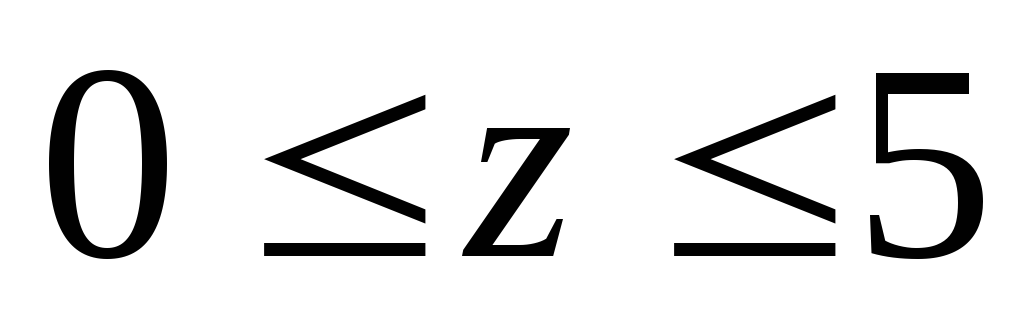
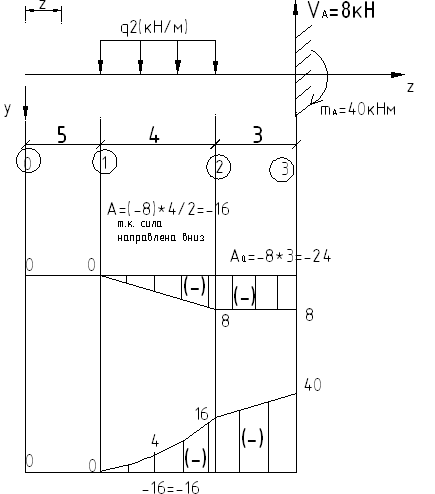
_{Q=0, M=0- свободный незагруженный конец балки}

_Уч.1-2,

_:

_:

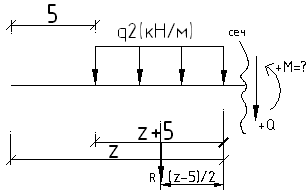
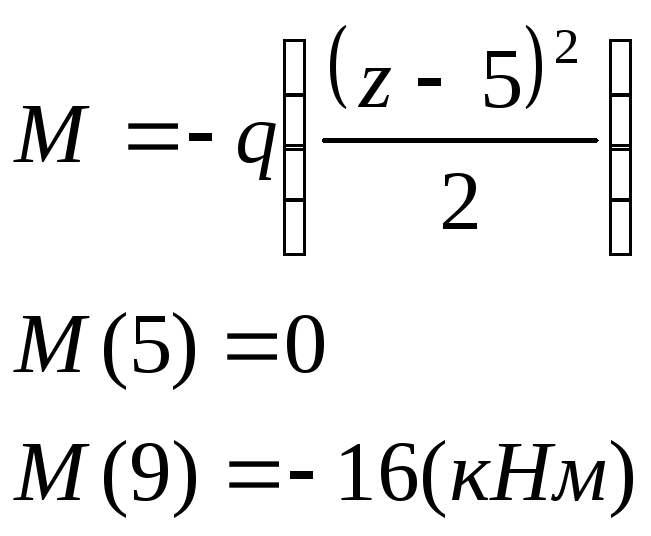
_Уч.2-3,

_РОЗУ

_:

_:

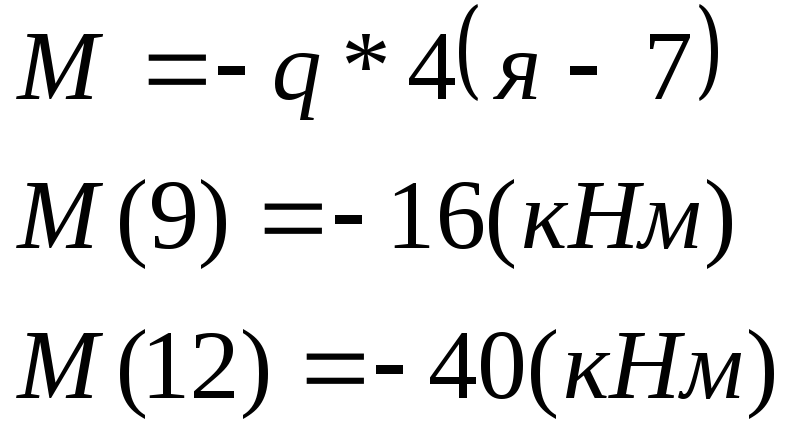
₃₎

_:

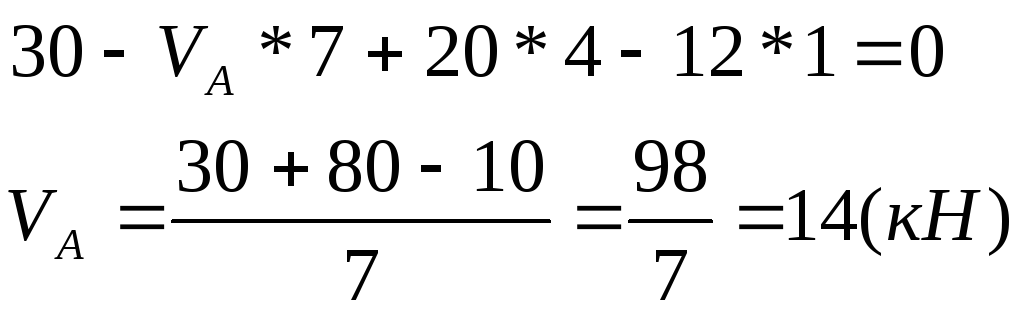
_{Откуда:}

_{Уч.0-1, ;}

_Уч.1-2,

_РОЗУ

_:

_:

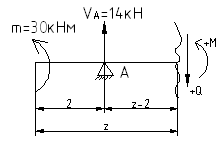
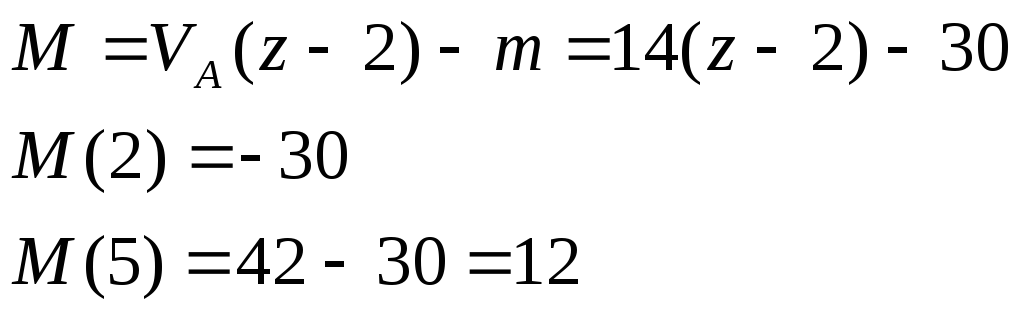
_Уч.2-3,

_РОЗУ

_:

_:

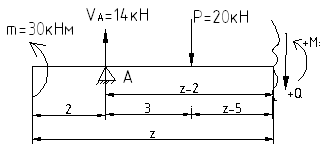
_Уч.3-4,

_РОЗУ

_:

_:

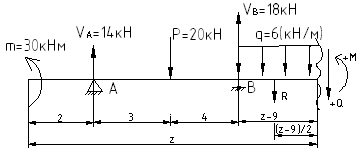
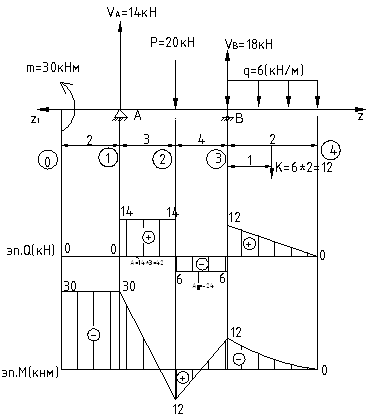
Лекция 12

_{Примеры построения эпюр М и Q в изгибаемых балках.}

_{Расчет изгиб балки на 2-х опорах}

_:

_:

_{Откуда:}

_Уч.0-1:

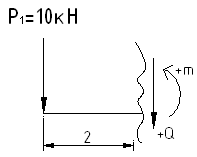
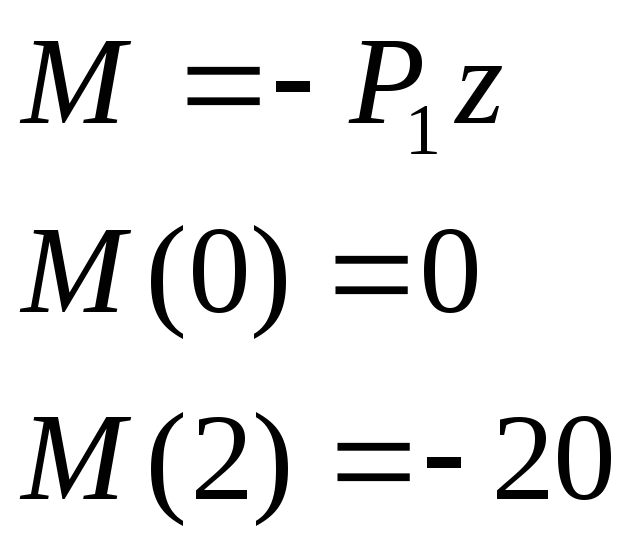
_РОЗУ:

_:

_:

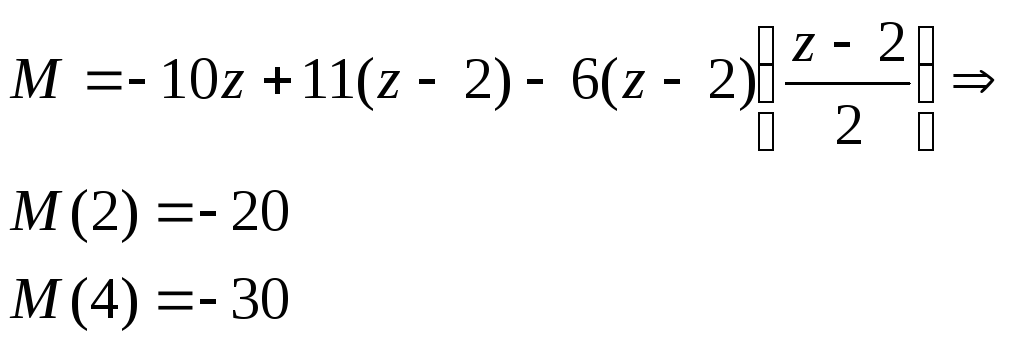
_Уч.1-2:

_:

_:

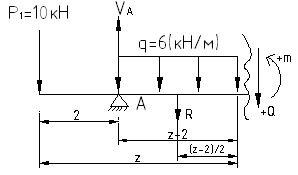
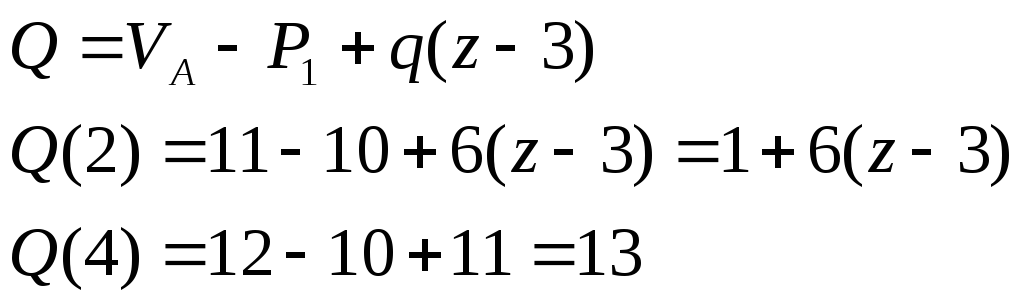
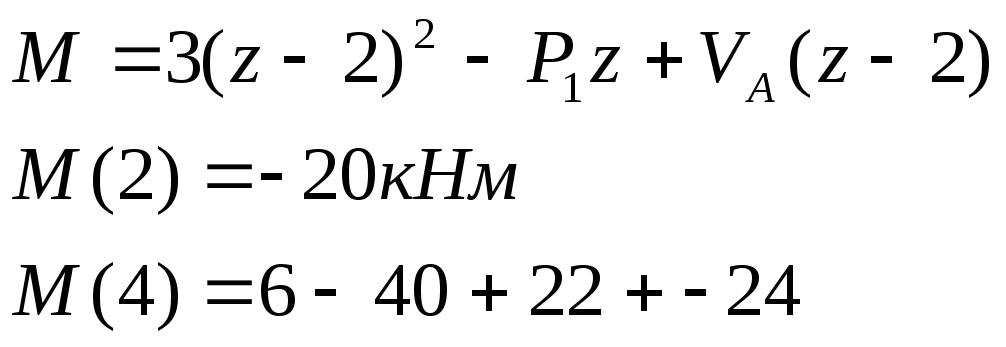
_Уч.2-3:

_РОЗУ

_:

_:

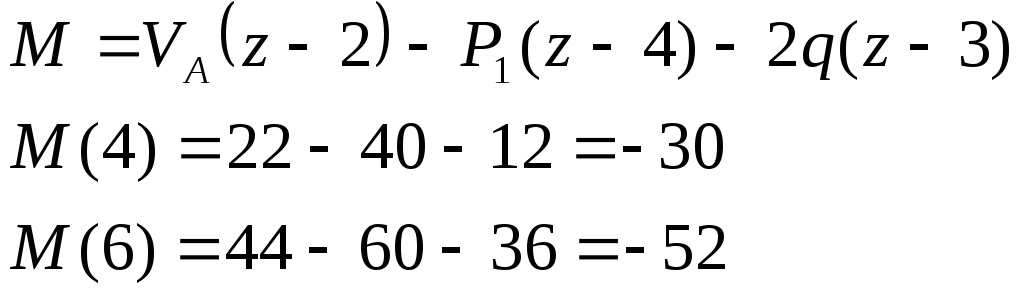
_{По эпюре М можно подобрать Mmax :}

_{Подбор поперечного сечения балки:}

_{- для проверки величин касательного напряжения балки}

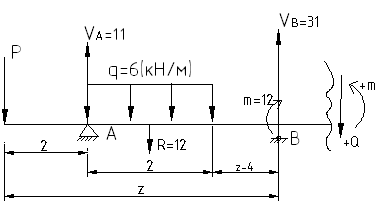
_{Расчет многопролетных статически определимых балок}

_{Пролет заключен между 2-мя наземными опорами балки (моста).}

_{В каждом промежуточном шарнире изгибающий момент отсутствует.}

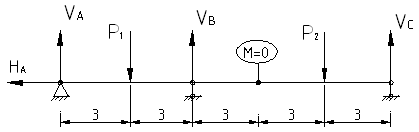
_{Составляем систему линейных алгебраических уравнений (СЛАУ) (N=4)}

_{Самый сложный путь решения задачи-}

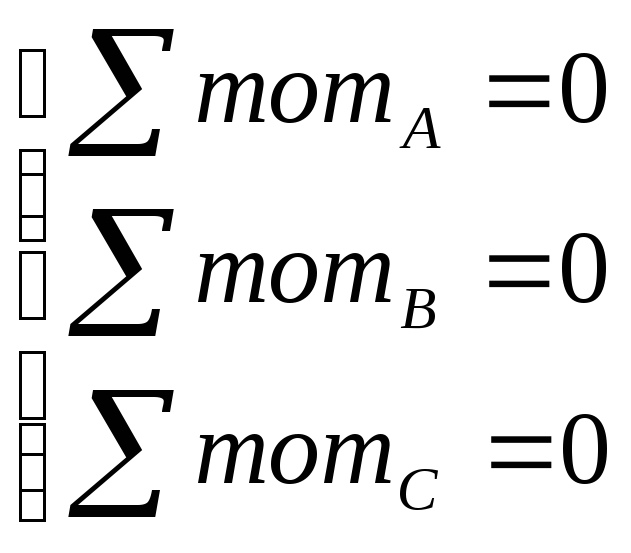
_{Отдельное нахождение неизвестных:}

_:

_{Правая часть балки была рассмотрена отдельно.}

_{Рассмотрим отдельно обе части балки.}

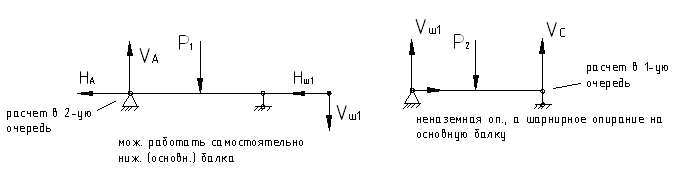
_{Используем закон Ньютона:}

_{при взаимодействии 2-х тел силы взаимодействия равны по величине и противоположны по направлению.}

_:

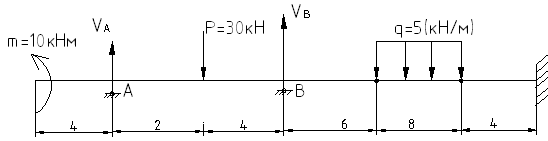
_{Рассмотрим отдельно каждую из частей балки}

_{Изображаем схему взаимодействия частей балки (поэтажную схему)}

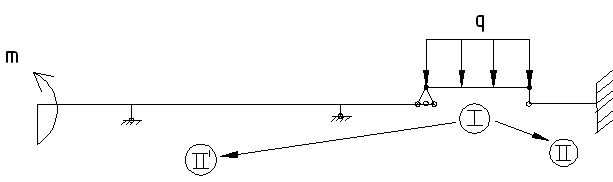
_{Начинаем расчет с верхней (вспомогательной) балки}

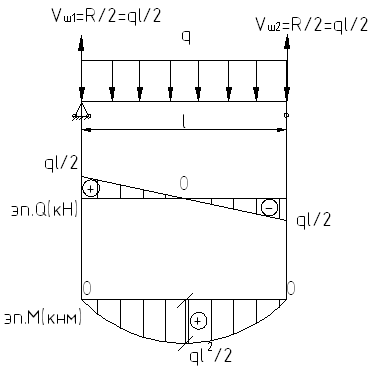
_РОЗУ:

_:

_:

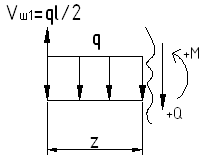
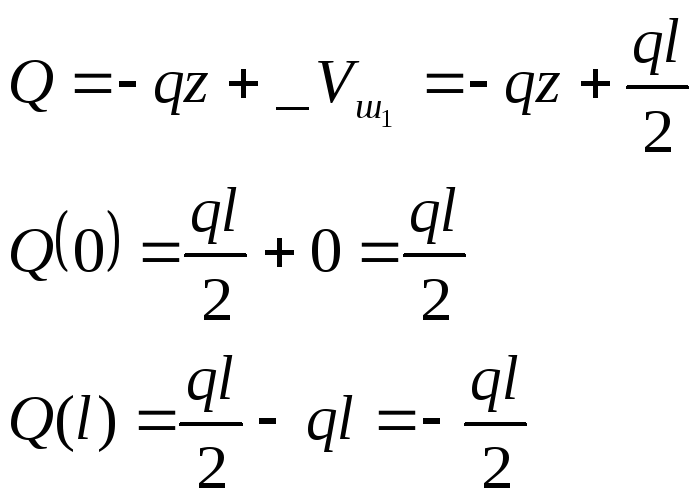
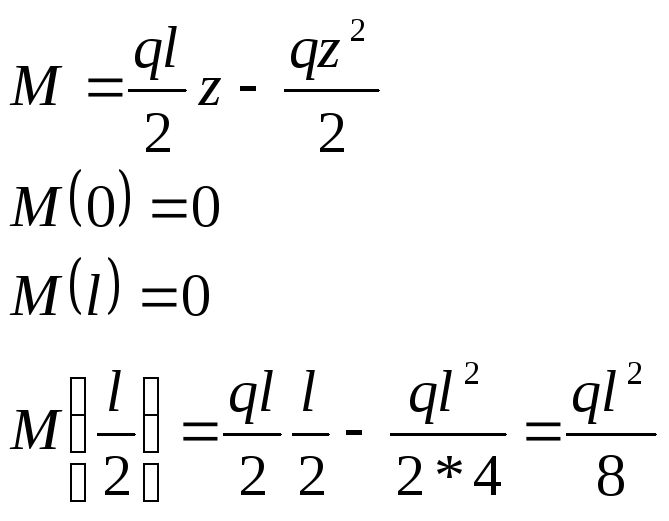
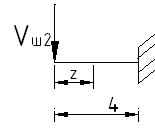
_{Рассчитаем правую основную балку.}

_РОЗУ:

_:

_:

_:

_:

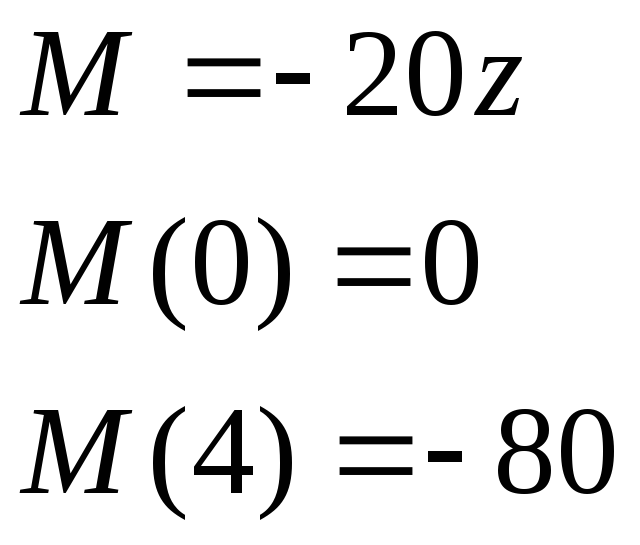
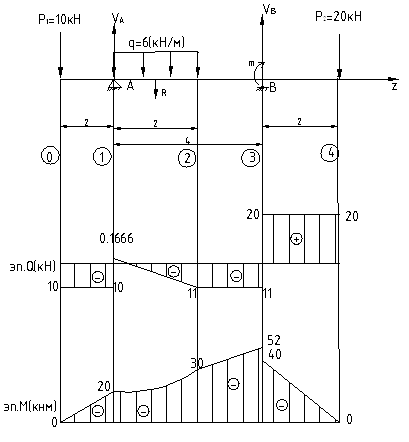
Соединим все эпюры на едином графике и получим окончательный вид эпюр Q и М:

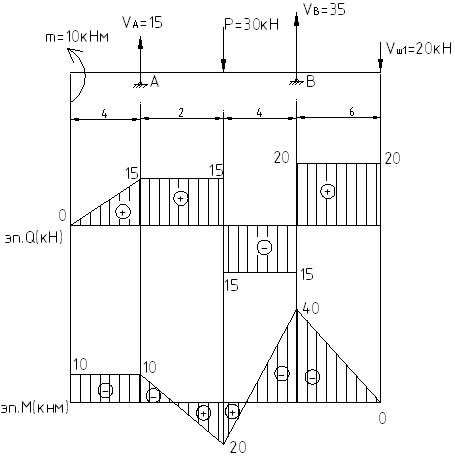
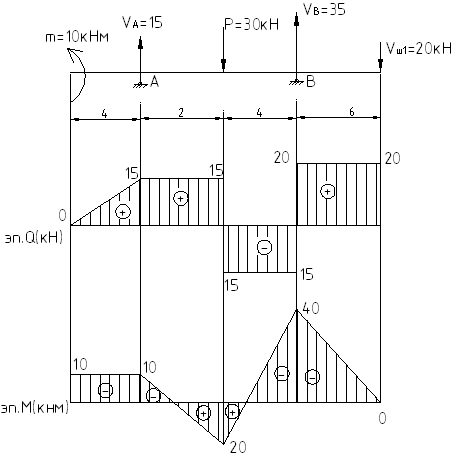
Лекция 13

_{РАСЧЕТ ИЗГИБАЕМЫХ БАЛОК НА ПРОЧНОСТЬ}

_{Рассмотрим конкретную балку.}

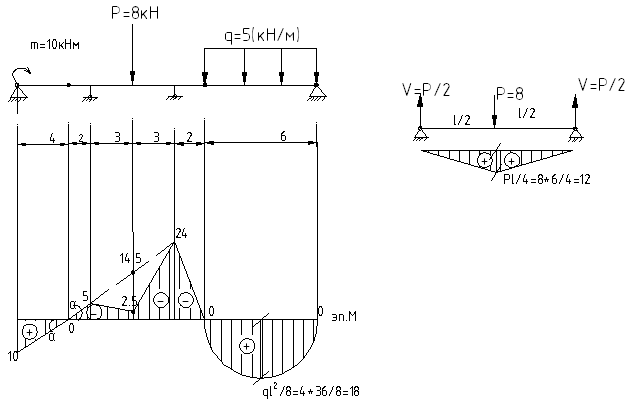
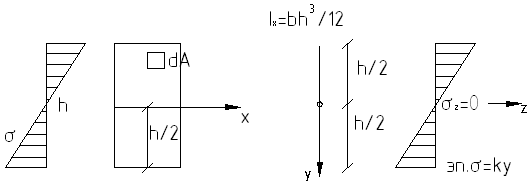
_{Выводим формулу для нормальных напряжений при изгибе. Из гипотез изгиба балок следует, что нормальное напряжение пропорционально вертикальной координате y:}

_{Изгибающий момент}

• 

_{- формула для нормального напряжения при изгибе.}

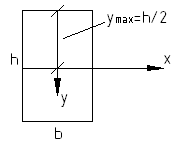
_{Вводим понятие момента сопротивления сечения при изгибе}

_{Для любого типа поперечного сечения балки должно быть}

_{В ГОСТе имеется двутавр І №16 ,І №18}

_{Проверим прочность I № 16:}

_{Перенапряжение составляет:}

_{- недопустимая величина перенапряжения}

_{Возьмем I №18:}

_,

_{Рассмотрим балку из одного швеллера}

_{Необходимо изготовить сечение из 2-х швеллеров.}

_{Берем швеллер [ №14:}

_,

_{[] Wx=140.4см}³_{, A[]=31.2см}²

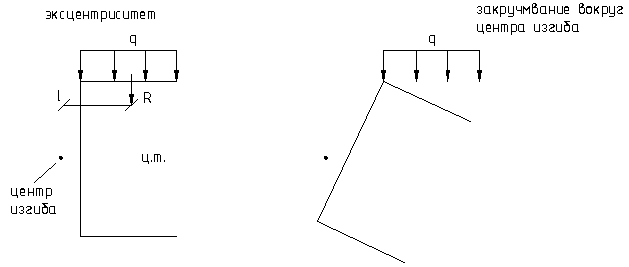
_{Рассмотрим современное коробчатое сечение балки.}

_Wx=120см³

_{Для балок обычно принимается:}

_h=3b

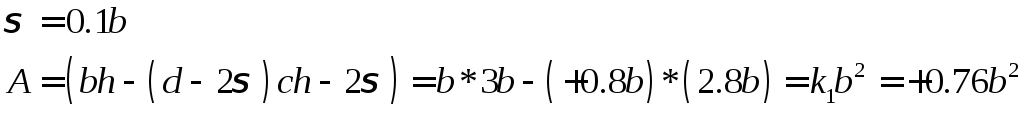
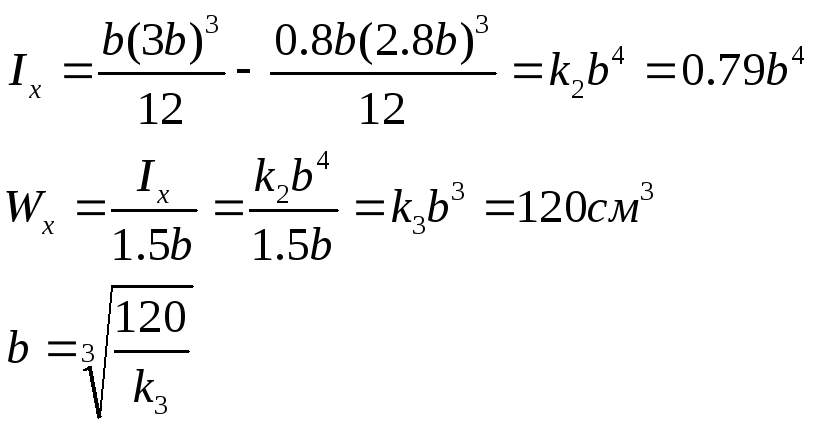
_{Рассмотрим кольцевое поперечное сечение балки (трубчатое)}

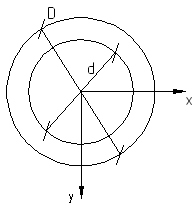
_{α- коэффициент тонкостенности}

Рассмотрим прямоугольное поперечное сечение балки

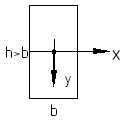
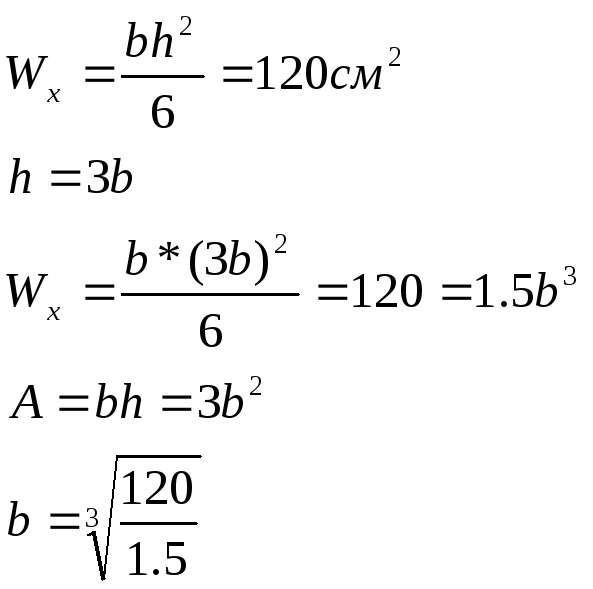
Рассмотрим квадратное поперечное сечение балки

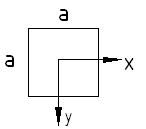
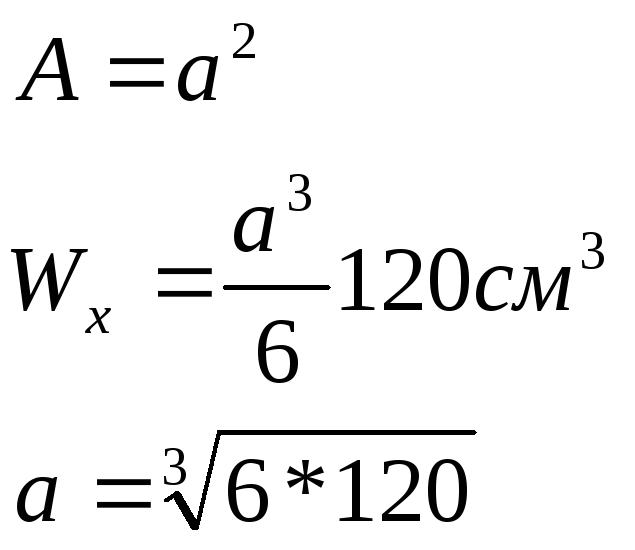
_{Рассмотрим круглое поперечное сечение балки}

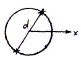
_{Сравниваем все типы поперечных сечений по расходу материала пропорционального площади поперечных сечений}

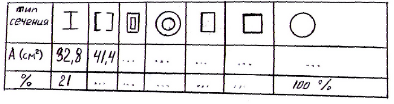
_{Рассмотрим вопрос о рациональности распределения материалов в различных типах поперечных сечений.}

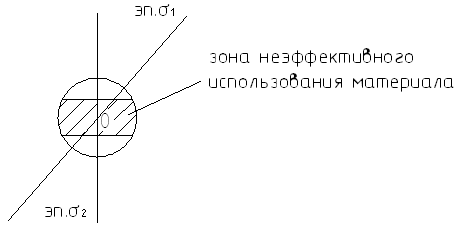
_{Нужно стремиться, чтобы в этой зоне было как можно меньше материала.}

_{Таким образом, наиболее экономичны при изгибе балок те поперечные сечения, у которых материал максимально разнесен от нейтральной оси, вблизи от которой он используется неэффективно.}