Лекция 7

_{Оптимизация статически неопределимых систем}

_{Основные параметры оптимизации:}

_{- стоимость}

_{- расход конструкционных материалов}

_{- сроки возведения}

_{Займемся вопросом о расходе материала}

₍₂₎

_{, (3)}

_:

(**)

Обеспечиваем равнопрочность стержней 1 и 2

_(*)

_:

₍₁₎

_{Полученное равенство дает возможность сформулировать условие равнопрочности для статически неопределимых систем: В равнопрочных стержневых системах отношение длины вертикальной подвески к ее расстоянию от шарнирно-неподвижной споры - величина постоянная.}

_{Рассмотрим пример системы с несколькими подвесками}

_{Предположим, что система будет равнопрочной, т.е. соблюдается условие}

_{Выясним вопрос о возможности повышения несущей способности системы.}

_{Предположим, что:}

_{в первом стрежне площадь поперечного сечения А1 , а , тогда ;}

_{во втором стержне площадь поперечного сечения А2 , а , тогда}

_{Получим: .}

_:

_{а1нов=2а 1; а2нов=2а2}

_{Pнов = 2P, что дает возможность сделать важный вывод:}

_{При пропорциональном увеличении расстояний от стержней подвески до опоры пропорционально растет несущая способность системы.}

_{При увеличении плеча одного из стержней несущая способность также возрастает.}

_{Расход материала определяется:}

_{V = A * l}

_{Если стержень с постоянными A и l перемещать вдоль абсолютно жесткого бруса, то объем остается постоянным. Следует добиваться наибольшего плеча силы P относительно шарнирно-неподвижной опоры А.}

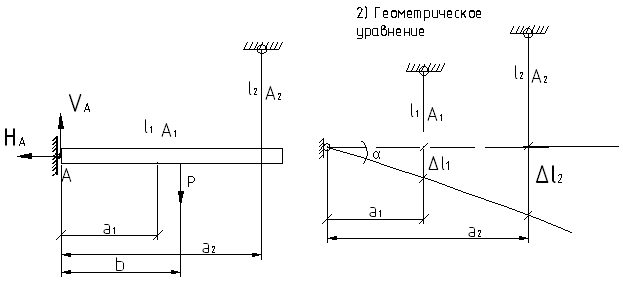
_{Задача:}

1. _{AB = a1*sinα}

_{AC = a2*sinα}

_{0 = N1*AB+N2*Al-Pb (І)}

2. _{Геометрическая сторона задачи:}

_{(І І)}

_{(І І І)}

_{a1*sinα1 = AB = ρ1}

_{a2*sinα2 = AB = ρ2}

_{, где ρ – плечо относительно шарнирно-неподвижной опоры.}

_{Полученное равенство дает возможность сформулировать условие равнопрочности для статически неопределимых систем с произвольным углом ориентирования повесок:}

_{В равнопрочной статически неопределенной системе отношение длины конкретного стержня к плечу усилия в нем относительно шарнирно-неподвижной опоры – величина постоянная.}

Лекция 8

_{Геометрические характеристики плоских сечений}

_{Первой геометрической характеристикой является площадь поперечных сечений А (м}²_{). Для вычисления площади необходимо:}

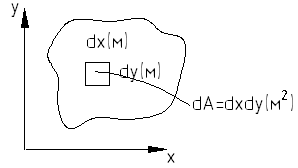
_{(1) Сложные фигуры можно представить в виде набора треугольников:}

_{Рассмотрим вопрос о площадях и положения центра тяжести элементарных фигур.}

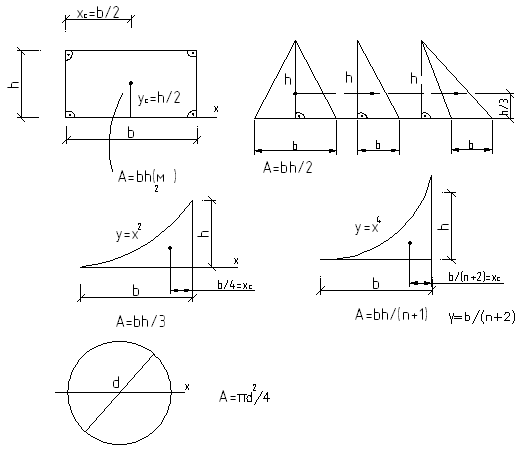
_{Кроме площади поперечного сечения существует еще ряд геометрических характеристик, входящих в подавляющее число расчетных формул сопротивления материалов, напроимер:}

_,

- осевой момент инерции сечения

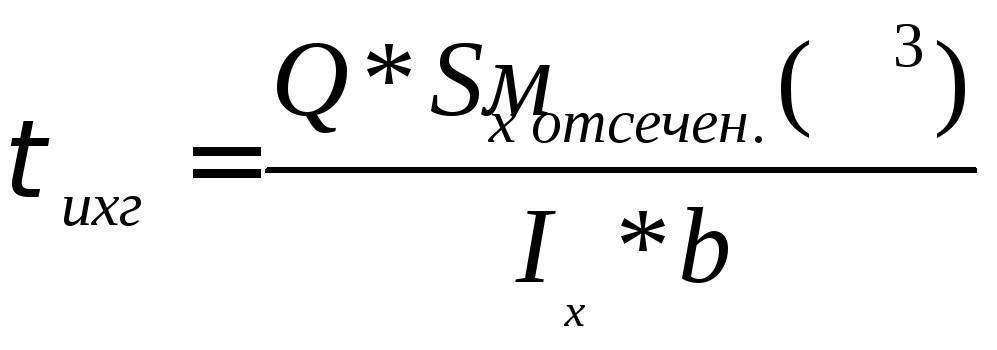
_{Рассмотрим статические моменты площади сечения А (м}²₎

_{-статический момент площади относительно х (2)}

_{-статический момент площади относительно оси y. (2.1)}

_{Рассмотрим пример вычисления величины статического момента для прямоугольного поперечного сечения с габаритами b (ширина) и h (высота).}

_{(*) ,}

_(3.1)

_(3.2)

_{По известному свойству определённого интеграла}

_{- если составляющие сложной фигуры элементарны, то можно воспользоваться формулой (*), например}

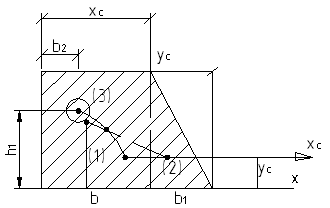
_{Рассмотрим пример:}

₍₁₎

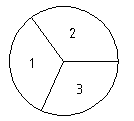
_{Общий алгоритм поиска координат центра тяжести сложной фигуры включает в себя следующие пункты:}

_{- выбираем удобную для данной задачи систему координат XOY}

_{- разбиваем сложную фигуру на элементарные составляющие}

_{- определяем для каждого элемента фигуры ее площадь Ai и расстояние от ее центра тяжести до осей X и Y; Xi, Yi}

_{-подсчитвыаем величины статических моментов}

_,

_{- ,}

_{- откладывая отрезки xc и yc и проводя соответствие оси, определяем координаты центра точки сложной фигуры.}

_{Моменты инерции поперечных сечений}

_{- осевой момент инерции сечения относительно OX (4.1)}

_{-осевой момент инерции сечения относительно OY (4.2)}

_{-центробежный момент инерции (4.3)}

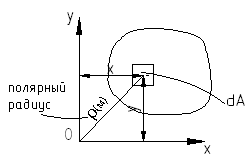
_{- полярный момент инерции (4.4)}

_{Вычислим величину момента инерции для прямоугольного поперечного сечения:}

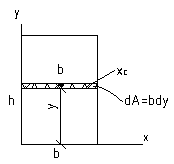
_{Вычислим IXc относительно оси, проходящей через центр тяжести сечения:}

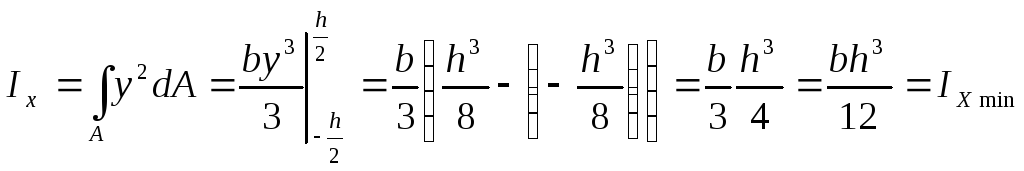
_{Момент инерции сечения относительно центральной оси меньше величин моментов инерции относительно любых других параллельных осей.}

_{Сводка формул для величин моментов инерции элементарных фигур.}

_{Прокатные профили:}

_{- двутавр}

_{- швеллер}

_{- уголок: равнобокий, неравнобокий}

_{- лист}

_{- z-образный профиль}

_{- широкополочный двутавр и т.д.}

_{На каждый прокатный профиль существует ГОСТ.}

_{На каждый тип профиля существует сортамент.}

1. _{Двутавр}

_{ГОСТ дает: h,b,d,A,вес 1 погонного метра, Ix, Sx, ix, Iy, Sy, iy.}

_{Таблица сортаментов позволяет выбрать требуемый № профиля двутавра.}

2. _{Швеллер}

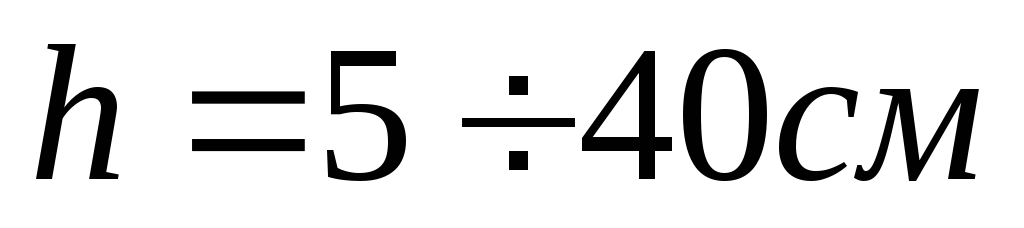
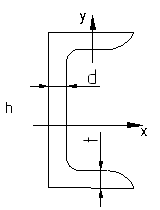
_{В дополнение к величинам у двутавра, здесь дополнительно задается величина Z0 - расстояние от наружной поверхности стенки до центра тяжести швеллера.}

_{Уголок равнобокий}

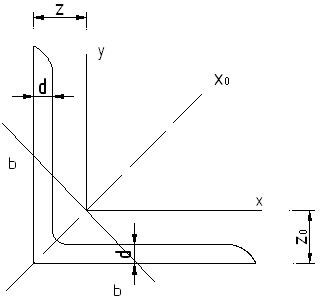
_{- различные толщины стенки при постоянном габарите уголка}

3. _{Уголок неравнобокий}