Лекция 9

_{В практике проектирования необходимо вычислять положение центра тяжести сложного поперечного сечения и моменты инерции сечения относительно центральной оси сечения.}

_{У каждой фигуры есть свои собственные оси, от которых необходимо перейти к общим осям.}

_{Рассмотрим формулы для моментов инерции сечения при параллельном переносе осей.}

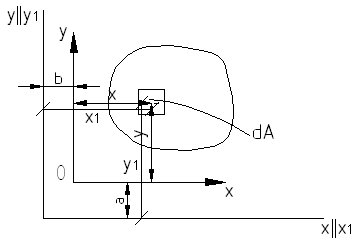
_{Формула для момента инерции относительно оси Х1:}

_{В частном случае второе слагаемое в формуле обратится в ноль - Sx=0: yc=0- ось Х проходит через центр тяжести сечения и является осью симметрии.}

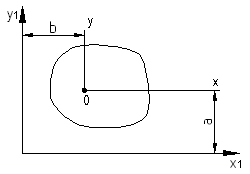
_{X и Y – центральные оси частной фигуры.}

_{X1 и Y1- центральные оси всей фигуры.}

_(1,1)

_(1,2)

_(1,3)

_{В практике проектирования встречаются следующие задачи:}

_{При заданном расходе материала обеспечить требуемые геометрические характеристики поперечного сечения.}

_{Здесь решается задача рационального проектирования.}

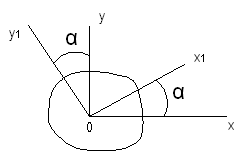
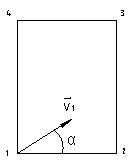
_{2-я возможная задача: обеспечивает требуемые геометрические характеристики сечения при минимальном расходе материала (задача оптимизации). При этом возникает потребность записи величин моментов инерции при повороте осей на некоторый угол α.}

_(2.1)

_(2.2)

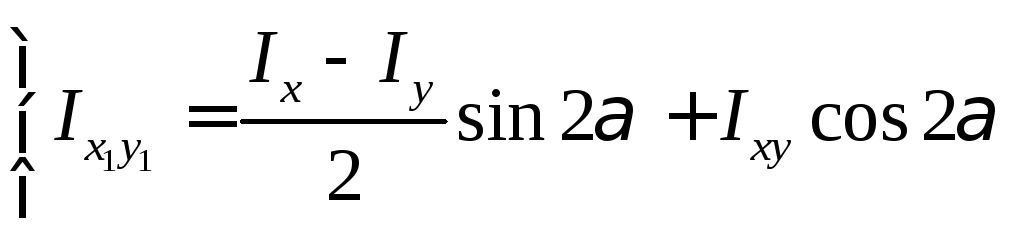_(2.3)

_{Ставим задачу поиска такого , при котором}

_{, ,}

_{Используем уравнение (2.3) и получаем:}

_,

_{, (2.4)}

_{Рассмотрим сечение, у которого}

_{Если , тогда:}

_{Величина угла α0 во всех случаях, когда подсчитывается по формуле (2.4)}

_{При повороте на данный угол один из моментов инерции становится максимальным, а другой минимальным.}

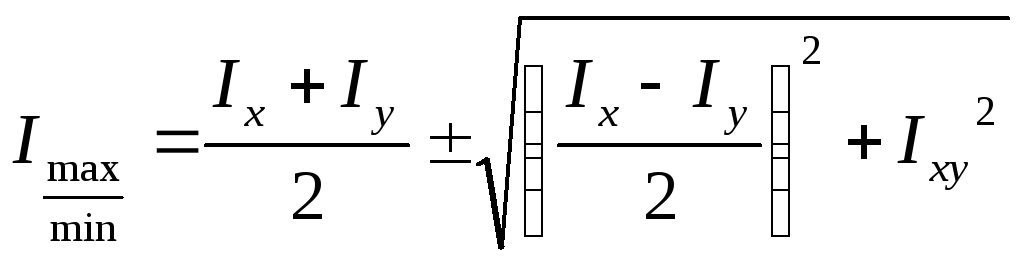₍₅₎

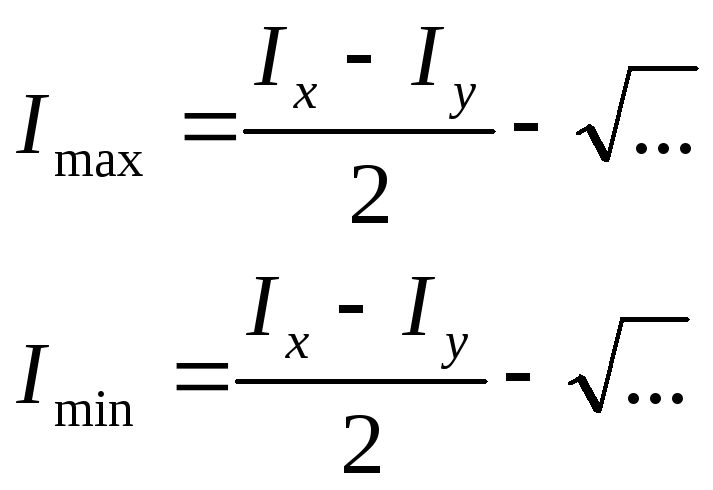
(6)

При этом ось x₁ перпендикулярна оси y_1.

Сумма двух осевых моментов инерции относительно ортогональных осей – величина постоянная

_{В современных расчетах случается следующие варианты:}

1. _{За строго ограниченное время необходимо сравнивать несколько проектных решений и выбрать оптимальное}

2. _{Обеспечить минимальный расход материалов при соблюдении всех необходимых требований к проекту}

_{Для решения этих задач существуют современные методики вычисления геометрических характеристик плоских сечений.}

_{Использование векторной алгебры для подсчетов величин геометрических характеристик плоских сечений}

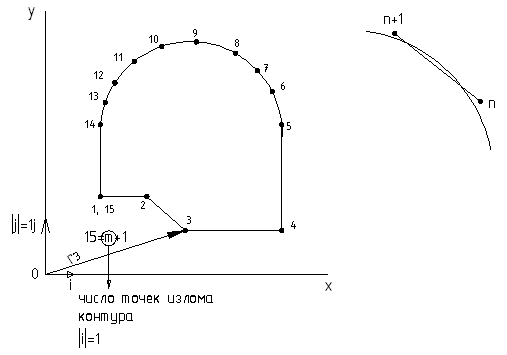
_{Выбираем удобную систему координат XOY}

_{Проводим в каждой точке излома контур R-вектор из начала координат.}

_{Вектор полностью определяется числами х3 и у3}

_{Для задания І:}

_{FOR І:=1 to 15 READLN (x(І); y(І));}

_{После ввода координат всех точек излома контура информация полностью введена.}

_{Далее ПЭВМ считает по программе с использованием формул векторной алгебры:}

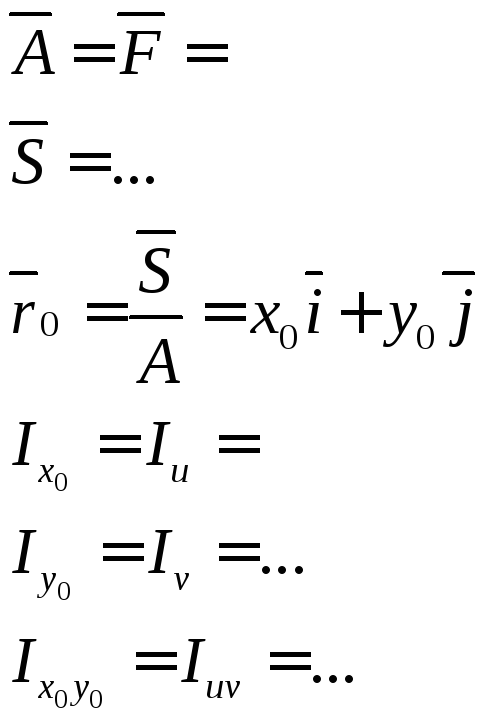
_{Далее ПЭВМ вычитает величины, указанные в формуле (4) , и величины:}

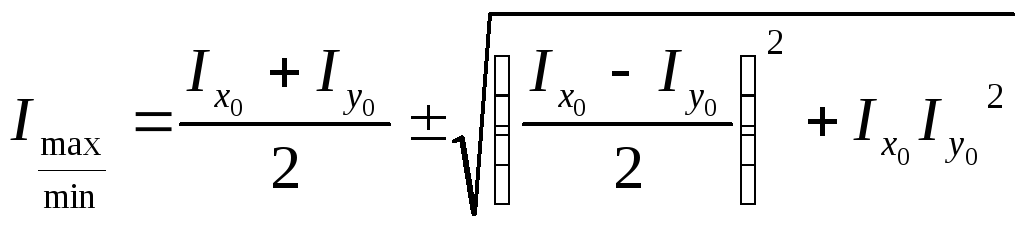
_{С использованием данной методики могли быть решены реальные задачи проектирования мостов и тоннелей.}

_{Рассмотрим поперечное сечение подводного тоннеля}

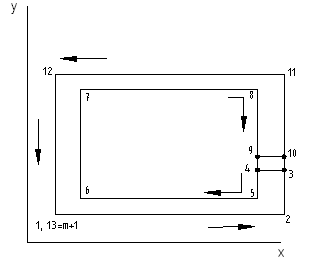
_{Ширина разреза может быть назначена в зависимости от точности масштаба.}

_{Если встречные потоки разделены, то тоннель может иметь следующую конфигурацию.}

_{В современных условиях эксплуатации на материал конструкций действуют агрессивные среды. Рассмотрим использование программного обеспечения ПЭВМ для учета возникновения и развития коррозии на элементах сечений.}

_{Для каждого района задается величина скорости коррозии}

_{В результате можно поставить следующую задачу во времени t:}

_{Обычно в условиях действия агрессивной среды происходит отслоение защитного слоя бетона и коррозия арматуры.}

_{Можно подсчитать время надежной эксплуатации конструкции.}

_{Рассмотрим двутавровое поперечное сечение.}

_{Приводим для него относительные скорости распределения коррозии по элементам сечения.}

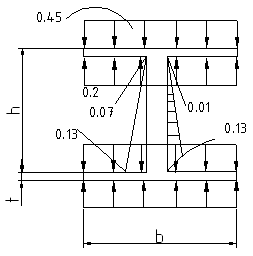
_{Эпюра коэффициентов скоростей коррозии по элементам профиля}

_{Поперечное сечение должно быть проверено на момент времени t=t1,t2 с целью проверки выполнения условия:}

_Ix(t)>Ixmin.

_{В стальных мостовых конструкциях коррозия недопустима, поэтому при появлении ее признаков пятно коррозии зачищается до здорового металла с помощью пескоструйного аппарата и проводится окраска поверхности защитными грунтовками и красками.}