Лекция 14

_{Определение перемещений при изгибе балки}

_{В сопротивлении материалов перемещение определяется по формуле О. Мора:}

₍₁₎

_{Формула Отто Мора}

_{М(z)i- аналитическое выражение для изгибающего момента на этом участке балки}

- аналитическое выражение для единичного изгибающего момента _{на этом участке балки}:

а) если требуется определить прогиб в конкретном сечении балки:

прикладываем единичную силу Р=1 в данном сечении и строим эпюру единичных моментов

_{б) в случае определения угла поворот в сечении прикладывается в данном сечении единичный момент m=1} и строится эпюра единичных моментов

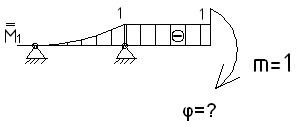
_{После этого необходимо вычислить величину определенного интеграла по формуле (1).}

_{Рассмотрим конкретный пример определения прогиба.}

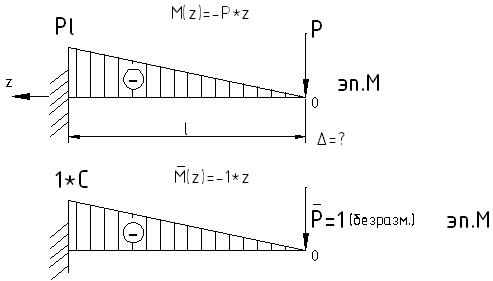
_{Если у балки много участков с различной нагрузкой, то вычисления по формуле (1) затруднительны.}

_{Формула Симпсона для определения перемещений:}

₍₂₎

_{Формула Симпсона дает точные величины перемещений, если эпюра М является параболой второй степени (всегда реализуется при действии равномерно распределенных нагрузок), а эпюра единичных моментов – ломаной прямой (реализуется всегда).}

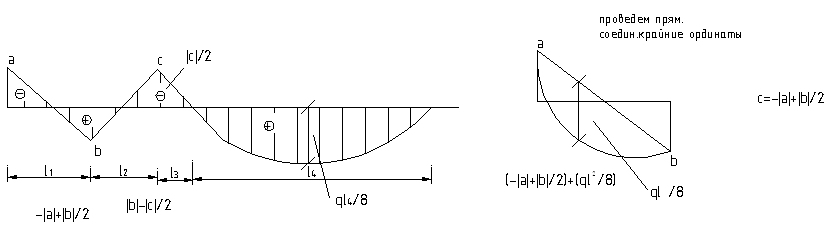
_{Среднее значение моментов определяется элементарно по формуле (3)}

₍₃₎

_{Рассмотрим тот же пример, который решаем с использованием формулы Симпсона:}

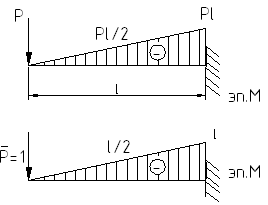
_{- совпадает с результатом по интегралу Мора.}

Рассмотрим пример определения перемещений в балке.

_{При построении эпюры изгибающих моментов используем принцип суперпозиции (эффект независимости действия си)}

_{Эпюра единичных моментов, построенная для определения прогиба в середине балки, имеет следующий вид:}

_{Определяем прогиб в середине балки по формуле Симпсона:}

_{2) Рассмотрим пример определения угла поворота сечения балки}

_{Определяем угол поворота на правой опоре балки}

_{Угол поворота}

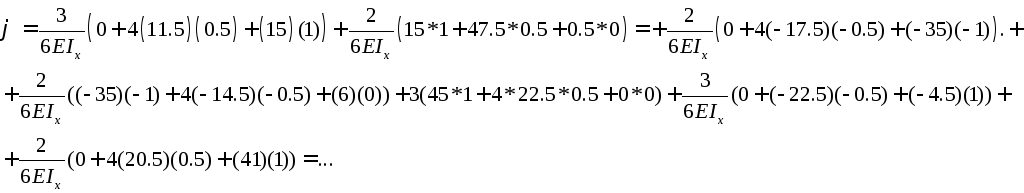
_{Во всех вышеприведенных вычислениях моменты записывались в (кН/м). На самом деле нужно писать в базовых единицах (Н*м), поэтому во всех вышеприведенных вычислениях умножаем полученные величины перемещений на 10}³_.

_{Рассмотрим расчет балки на жесткость (по второму предельному состоянию). Считаем, что прогиб мостовой балки не может превышать 1/450 от ее пролета. Берем конкретный пример расчета.}

_{Берем I №30:}

_{Поверим данный двутавр на прочность:}

_{Что соответствует двутавру I №18а.}

_{Таким образом, двутавр № 30, подобранный из условия требуемой жесткости балки, удовлетворяет и условиям прочности балки.}

Лекция 15

_{Кручение валов круглого и кольцевого поперечного сечения}

_{Закручивание валов вызывается моментами, действующими в плоскостях, перепендикулярных оси валов.}

_{Проведем опыт над валом из резиноподобного материала}

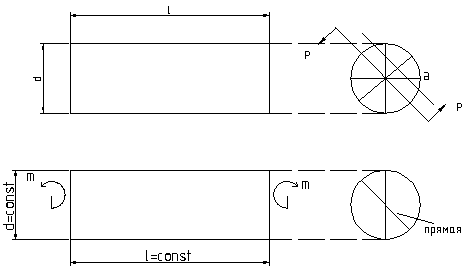
_{- закручивающий момент}

_{φ- угол закручивания}

_{В результате анализа данных опытов устанавливается:}

1. _{Длина вала при кручении остается постоянной l=const}

_{∆l(z)=0 –приращение}

₍₁₎

_{- нормальные напряжения на площадках, перпендикулярных оси вала, отсутствуют.}

_{2) В поперечном сечении вала d=const}

_∆d=0

_{(2) на любой площадке, параллельной оси вала, нормальные напряжения равны нулю.}

_{3)Все диаметральные линии в поперечных сечениях остаются прямыми, повернувшись на некоторый угол.}

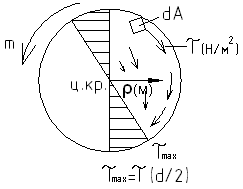
_{τ- касательные напряжения в поперечном сечении вала}

_{ρ- полярный радиус конкретной точки поперечного сечения}

_{(3)- касательные напряжения изменяется линейно с ростом расстояния от центра круга.}

_{Записываем формулу для крутящего момента. Выделяем элементарную площадку dA, по которой действует напряжение τ.}

₍₄₎

_{Определение: крутящим моментом M (кН*м) в данном сечении вала называется внутренней силовой фактор (формула (4)), численно равный алгебраической сумме закручивающих моментов по одну сторону от данного сечения вала.}

_{Эпюра Мкр при действии сосредоточенных закручивающих моментов имеет постоянные ординаты на каждом участке вала, и под каждым внешним моментом происходит скачок на величину данного момента.}

_{Используя эпюру Мкр , можно подобрать поперечное сечение вала. С использованием формул (3), (4) выводим формулу для касательных напряжений вала.}

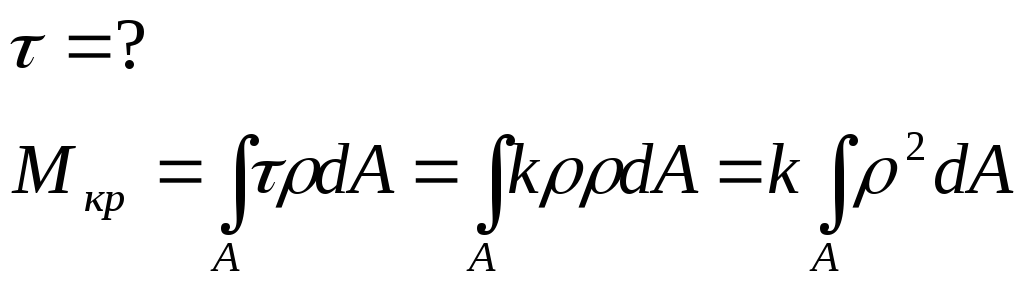
₍₅₎

_{По аналогии с изгибом вводим величину Wρ – полярного момента сопротивления сечения.}

₍₆₎

_{Для круглого поперечного сечения:}

_,

_Тогда:

_{По ГОСТу диаметры валов идут с определенными шагами:}

_{d= 30мм, 35,40,45,50,55,60,65,70.75.80,85,90,95,100мм,…}

_{d= 79.8мм}

_{Принимаем из условия прочности диаметр вала d= 80мм}

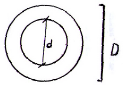
_{Докажем, что вал кольцевого поперечного сечения экономичнее по расходу материала вала кругового поперечного сечения.}

D=90мм

d= 0.7*90=63мм

Возьмем d=65мм

• Площадь кольцевого поперечного сечения:

Расход металла пропорционален площади, для вала кольцевого поперечного сечения экономия металла составляет

Кроме того, при использовании кольцевого поперечного сечения металл удаляется из той части вала, где напряжение τ мало, т.е. металл используется в этой зоне неэффективно.

Расчет валов на жесткость

В зависимости от скорости вращения вала нормируется угол закручивания вала в градусах на один погонный метр вала, что соответствует расчету вала на жесткость.

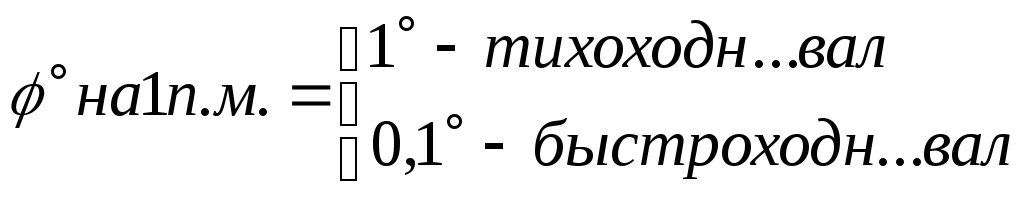
По аналогии с формулой для удлинений бруса при изгибе (м)

может быть записана формула для угла закручивания вала .

В данную формулу входит величина модуля сдвига, для которого теоретическое значение подсчитывается по формуле

(для стали),

где μ- коэффициент Пуассона, Е – модуль Юнга.

В градусной мере угол закручивания равен

Предположим, что

Отсюда можно получить величину I_ρ:

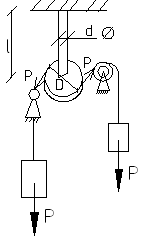
Опыт по определению модуля сдвига может быть проведен следующим образом:

=>

• .

В опыте замеряется угол закручивания при различных значениях нагрузки Р. Так как величиныиd известны, то можно подсчитать ряд значений модуля сдвига G и далее, вычислив среднее арифметическое данных значений, определить достоверную величину модуля сдвига для исследуемого материала.